Toptailieu.vn biên soạn và giới thiệu Phương pháp giải Giá trị tuyệt đối của một số hữu tỉ (50 bài tập minh họa) hay, chi tiết nhất, từ cơ bản đến nâng cao giúp học sinh nắm vững kiến thức về hỗn số, từ đó học tốt môn Toán 7.

Phương pháp giải Giá trị tuyệt đối của một số hữu tỉ (50 bài tập minh họa)

I. LÝ THUYẾT:

Giá trị tuyệt đối của một số hữu tỉ x, kí hiệu |x| là khoảng cách từ điểm x đến điểm 0 trên trục số.

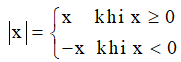
II. CÁC DẠNG BÀI TẬP CƠ BẢN:

Dạng 3.1: Tính toán các số hữu tỉ có chứa dấu giá trị tuyệt đối.

1. Phương pháp giải:

- Định nghĩa giá trị tuyệt đối của một số hữu tỉ:

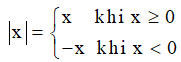
- Tính chất hay sử dụng của giá trị tuyệt đối:

$\forall x\in Z: \left|x\right|\ge 0;\left|x\right|=\left|-x\right|;\left|x\right|\ge x$

2. Ví dụ minh họa:

Ví dụ 1: Tính:

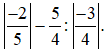
Giải:

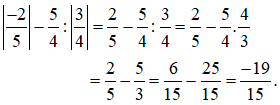
Dạng 3.2: Tìm một số chưa biết trong biểu thức có chứa dấu giá trị tuyệt đối.

1. Phương pháp giải:

- Áp dụng định nghĩa dấu giá trị tuyệt đối của một số hữu tỉ.

- Quy tắc chuyển vế.

- Tính chất hay sử dụng của giá trị tuyệt đối:

$\forall x\in Z: \left|x\right|\ge 0;\left|x\right|=\left|-x\right|;\left|x\right|\ge x$

2. Ví dụ minh họa:

Ví dụ 2: Tìm x, biết:

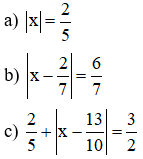
Giải:

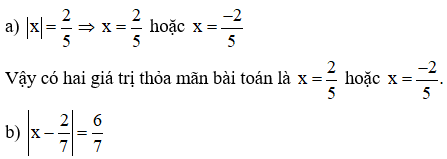
Cách 1: (Căn cứ vào định nghĩa của giá trị tuyệt đối)

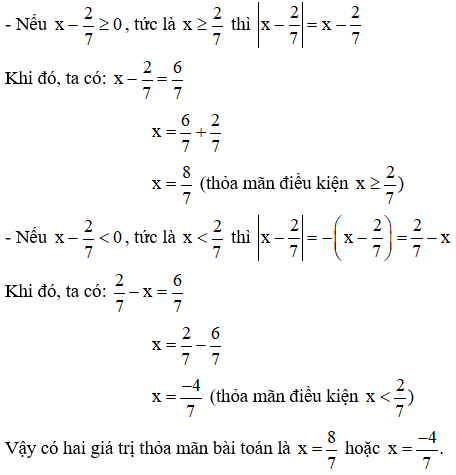
Cách 2: (Căn cứ vào tính chất |x| = |–x|).

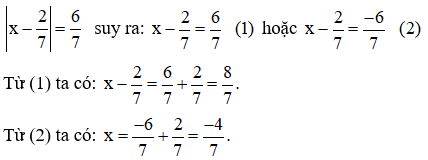
Dạng 3.3: Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức có chứa giá trị tuyệt đối.

1. Phương pháp giải:

Cho biểu thức A thì |A|$\ge 0$ với m là hằng số, ta có:

+ Giá trị nhỏ nhất của |A| + m ≥  m.

+ Giá trị lớn nhất của –|A| + m ≤ m.

2. Ví dụ minh họa:

Ví dụ 3: Tìm giá trị nhỏ nhất của biểu thức:

$A=\left|x-\frac{1}{3}\right|+4$

Giải:

Vì $\left|x-\frac{1}{3}\right|\ge 0\forall x$

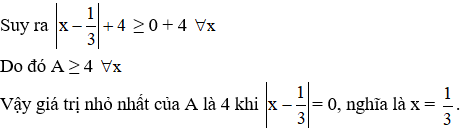
Ví dụ 4: Tìm giá trị lớn nhất của biểu thức:

B = 5,5 – |2x – 1,5|

Giải:

Vì |2x – 1,5| ≥ 0 $\forall x$

 => –|2x – 1,5| ≤ 0 $\forall x$

 => –|2x – 1,5| + 5,5 ≤ 5,5$\forall x$

 => 5,5 – |2x – 1,5| ≤ 5,5 $\forall x$

Suy ra B ≤ 5,5 $\forall x$

Vậy giá trị lớn nhất của B là 5,5 khi |2x – 1,5|= 0, nghĩa là 2x – 1,5 = 0 hay x = 0,75.

III. BÀI TẬP VẬN DỤNG:

Bài 1: Trong các khẳng định sau đây, khẳng định nào đúng:

a) |–10,5| = 10,5;

b) –0,75| = –0,75;

c) |–15,25| = – (–15,25).

Bài 2: Tính:

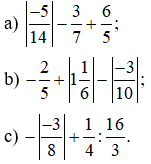
Bài 3: Tính giá trị của các biểu thức sau với: |a| = 1,5; b = –0,5.

a) A = a + b;                                     

b) B = 2a – |3b|.                       

Bài 4: Tìm x, biết:

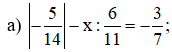
b) $\left|x\right|=\frac{1}{5}$

c) $\left|x\right|=\left|\frac{-4}{5}\right|$

Bài 5: Tìm x, biết:

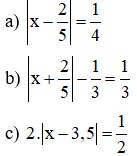
Bài 6: Tính giá trị biểu thức: A = 2x² – 5x + 1 biết |x| = $\frac{1}{3}$

Bài 7: Tìm giá trị nhỏ nhất của biểu thức:

a) A = |3,7 – x| + 2,5

b) B = |x + 1,5| – 4,5

Bài 8: Tính giá trị lớn nhất của biểu thức:

a) $M=2-\left|x+\frac{2}{3}\right|$

b)$N=-\left|x-\frac{2}{5}\right|+202$1

Bài 9: Tính giá trị của biểu thức:

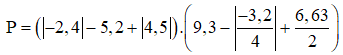
Bài 10: Tìm giá trị nhỏ nhất của biểu thức sau:

A = |x – 100| + |x – 400|

Hướng dẫn giải:

Bài 1:

a) Đúng (Vì –10,5 < 0 nên |–10,5| = –(–10,5) = 10,5).

b) Sai (vì |–0,75| = – (–0,75) = 0,75);

c) Đúng (vì |–15,25| = 15,25 = – (–15,25)).

Bài 2: (Bỏ dấu giá trị tuyệt đối rồi tính toán như bình thường).

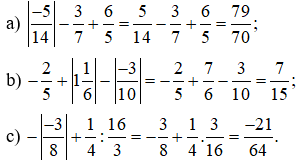
Bài 3:

a) Với a = 1,5; b = –0,5 A = a + b = 1

    Với a = –1,5; b = –0,5 A = a + b = –2

b) Với a = 1,5; b = –0,5 B = 2a – |3b| = 1,5

    Với a = –1,5; b = –0,5 B = 2a – |3b| = – 4,5            

Bài 4:

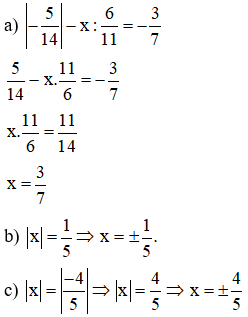
Bài 5: Tìm x, biết:

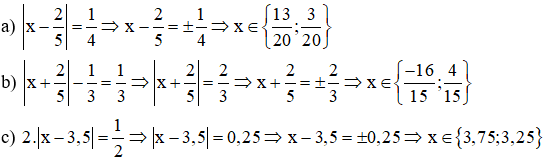
Bài 6: |x| = $\frac{1}{3}\Rightarrow x=\pm \frac{1}{3}$

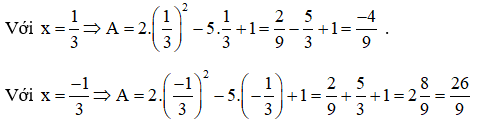
Bài 7: Giá trị nhỏ nhất của biểu thức:

a) A = |3,7 – x| + 2,5 ≥ 2,5. Dấu “=” xảy ra khi và chỉ khi x = 3,7

b) B = |x + 1,5| – 4,5 ≥ – 4,5. Dấu “=” xảy ra khi và chỉ khi x = –1,5

Bài 8: Giá trị lớn nhất của biểu thức:

a) $M=2-\left|x+\frac{2}{3}\right|$ ≤ 2. Dấu “=” xảy ra khi và chỉ khi x =

b)  $N=-\left|x-\frac{2}{5}\right|+2021$≤ 2021. Dấu “=” xảy ra khi và chỉ khi x =

Bài 9: Tính giá trị của biểu thức:

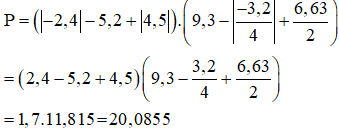
Bài 10:

Xem thêm các dạng Toán 7 hay, chọn lọc khác:

Các dạng toán về Tập hợp Q các số hữu tỉ và cách giải

Cách giải bài tập Cộng, trừ, nhân, chia số hữu tỉ cơ bản và nâng cao

Các dạng toán về Lũy thừa của số hữu tỉ và cách giải

Các dạng toán về Tỉ lệ thức và cách giải

Các dạng toán về Tính chất của dãy tỉ số bằng nhau và cách giải