Toptailieu.vn biên soạn và giới thiệu Phương pháp giải Công thức đổi phân số ra số thập phân (50 bài tập minh họa) hay, chi tiết nhất, từ cơ bản đến nâng cao giúp học sinh nắm vững kiến thức về hỗn số, từ đó học tốt môn Toán 7.
Phương pháp giải Công thức đổi phân số ra số thập phân (50 bài tập minh họa)
I. Lý thuyết
1. Đổi phân số ra số thập phân.
Muốn đổi một phân sốab(b≠0) ra số thập phân ta thực hiện phép chia a cho b
Khi chia a cho b ta được một trong hai trường hợp sau:
- Phép chia a cho b kết thúc ở hữu hạn bước:
Ví dụ:
a) 34 = 0,75
b)15= 0,2
Khi đó số thập phân thu được gọi là số thập phân hữu hạn tuần hoàn.
- Phép chia a cho b không bao giờ chấm dứt:
Ví dụ:
a)13 = 0,3333…
b)-711 = -1,5454…
Tuy phép chia không kết thúc nhưng phần thập phân của kết quả phép có một nhóm chữ số lặp đi lặp lại vô hạn lần. Ta nói số thập phân thu được là số thập phân vô hạn tuần hoàn.
2. Đổi từ số thập phân ra phân số
- Với số thập phân hữu hạn:
Bước 1: Ta đếm các số ở bên phải dấu phẩy.
Bước 2: Giả sử có n số bên phải dấu phẩy khi đó ta viết số thập phân thành phân số với tử số là số đã được bỏ đi dấu phẩy và mẫu số là 10n
Bước 3: Rút gọn phân số nếu có thể
- Với số thập phân vô hạn tuần hoàn:
Ta thừa nhận các kết quả:
0,(1) = 19
0,(01) =199
0,(001) = 1999
Ta xét các ví dụ sau:
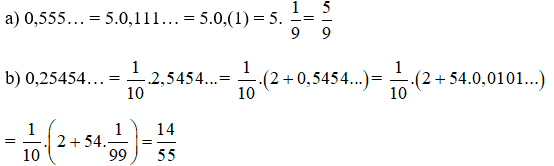
II. Các ví dụ:
Ví dụ 1: Viết các phân số sau dưới dạng số thập phân
a)6340
b)611
c)1345
Lời giải:
a) Ta lấy 63 chia 40 được kết quả là 1,575
Vậy 6340=1,575
b) Lấy 6 chia 11 ta được kết quả là 0,5454…
Vậy 611=0,(54)
c) Lấy 13 chia 45 ta được kết quả là 0,28888…
Vậy 1345=0,2(8)
Ví dụ 2: Viết các số thập phân sau dưới dạng phân số
a) 0,65
b) 1,3636…
c) 0,2(28)
Lời giải:

Xem thêm các dạng Toán 7 hay, chọn lọc khác:
Công thức tính giá trị tuyệt đối của một số hữu tỉ
Công thức lũy thừa của số hữu tỉ
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.