Toptailieu.vn biên soạn và giới thiệu Phương pháp giải Công thức về tính chất của tỉ lệ thuận (50 bài tập minh họa) hay, chi tiết nhất, từ cơ bản đến nâng cao giúp học sinh nắm vững kiến thức về hỗn số, từ đó học tốt môn Toán 7.

Phương pháp giải Công thức về tính chất của tỉ lệ thuận (50 bài tập minh họa)

I. Lý thuyết

1. Định nghĩa

- Nếu đại lượng y liên hệ với đại lượng x theo công thức y = kx (với k là hằng số khác 0) thì ta nói y tỉ lệ thuận với x theo hằng số tỉ lệ k.

Chú ý:

- Khi đại lượng y tỉ lệ thuận với đại lượng x thì x cũng tỉ lệ thuận với y và ta nói hai đại lượng đó tỉ lệ thuận với nhau.

- Nếu y tỉ lệ thuận với x theo hệ số tỉ lệ k thì x tỉ lệ thuận với y theo hệ số tỉ lệ $\frac{1}{k}$.

2. Tính chất

Nếu hai đại lượng tỉ lệ thuận với nhau thì:

- Tỉ số hai giá trị tương ứng của chúng luôn không đổi (bằng hệ số tỉ lệ):

$\frac{y_1}{x_1}=\frac{y_2}{x_2}=\frac{y_3}{x_3}=\mathrm{...}=\frac{y_n}{x_n}=k$(với k là hệ số tỉ lệ)

- Tỉ số giữa hai giá trị bất kỳ của đại lượng này bằng tỉ số giữa hai giá trị tương ứng của đại lượng kia:

$\frac{x_1}{x_2}=\frac{y_1}{y_2};\frac{x_1}{x_3}=\frac{y_1}{y_3};\mathrm{...}$

II. Các ví dụ:

Ví dụ 1: Cho x và y là hai đại lượng tỉ lệ thuận. Gọi $x_1$;$x_2$là hai giá trị của x thì $y_1$; $y_2$là hai giá trị tương ứng của y. Biết rằng $x_1$= 4; $x_2$= -10 và $y_1$ - $y_2$= 7.

a) Tính $y_1$;$y_2$

b) Biểu diễn y theo x.

Lời giải:

a) Vì x; y là hai đại lượng tỉ lệ thuận nên:

$\frac{y_1}{x_1}=\frac{y_2}{x_2}$. Thay $x_1$= 4; $x_2$= -10 vào ta có:

$\frac{y_1}{4}=\frac{y_2}{-10}$. Áp dụng tính chất dãy tỉ số bằng nhau ta có:

$$\begin{gathered} \frac{y_1}{4}=\frac{y_2}{-10}=\frac{y_1-y_2}{4-(-10)}=\frac{7}{14}=\frac{1}{2} \\ \Rightarrow \left\{\begin{array}{l}\frac{y_1}{4}=\frac{1}{2}\\ \frac{y_2}{-10}=\frac{1}{2}\end{array}\right.\Rightarrow \left\{\begin{array}{l}{y}_1=2\\ y_2=-5\end{array}\right. \end{gathered}$$

Vậy $y_1=2$; $y_2=-5$

b) Theo tính chất của tỉ lệ thuận ta có:

$\frac{y_1}{x_1}=\frac{y_2}{x_2}$= k

$\Rightarrow k=\frac{1}{2}$

Vậy đại lượng y biểu diễn theo đại lượng x là y = $\frac{1}{2}$x.

Ví dụ 2: Cho biết x và y là hai đại lượng tỉ lệ thuận.

a) Hãy xác định hệ số tỉ lệ của y đối với x.

b) Điền số thích hợp vào ô trống.

Lời giải:

a) Do x; y là hai đại lượng tỉ lệ thuận nên ta có: y = kx với $k\ne 0$.

$\Rightarrow k=\frac{y}{x}$. Theo đề bài ta thấy có một cột x = 6 và y = 2 thay vào ta có:

$k=\frac{y}{x}=\frac{2}{6}=\frac{1}{3}$

Vậy hệ số tỉ lệ của y đối với x là $\frac{1}{3}$.

b) Với $k=\frac{1}{3}\Rightarrow y=\frac{1}{3}x$.

Ta có:

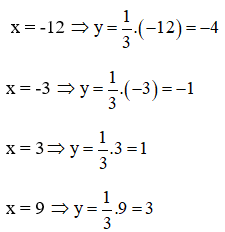
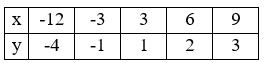
Ta có kết quả bảng sau:

Ví dụ 3: Cho 1 tấn nước biển thì chứa 25kg muối.

a) Giả sử x tấn nước biển chứa y kg muối. Hãy biểu diễn y theo x.

b) Hỏi 200g nước biển chứa bao nhiêu gam muối.

Lời giải:

Đổi 1 tấn = 1000kg

a) Vì số kg nước biển tỉ lệ thuận với số kg muối nên ta có:

y = kx     với k $\ne 0$

Thay x = 1000kg; y = 25kg vào công thức ta có:

25 = 1000.k

$\Rightarrow k=\frac{25}{1000}=\frac{1}{40}$

Biểu diễn y theo x là $y=\frac{1}{40}x$.

b) Với số gam nước biển là 200g nên x = 200g

Vậy số gam muối thu được là:

$y=\frac{1}{40}.200=5$(g)

Ví dụ 4: Chu vi của một tam giác là 34cm. Tính độ dài các cạnh của tam giác biết rằng chúng tỉ lệ thuận với 4; 5; 8.

Lời giải:

Gọi ba cạnh của là x; y; z (x; y; z > 0)

Vì chu vi tam giác là 34cm nên x + y + z = 34cm

Vì ba cạnh của tỉ lệ thuận với 4; 5; 8 nên ta có:

$\frac{x}{4}=\frac{y}{5}=\frac{z}{8}$

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

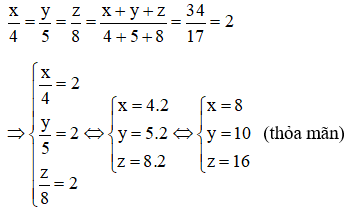
Vậy độ dài ba cạnh tam giác lần lượt là 8cm; 10cm; 16cm.

Xem thêm các dạng Toán 7 hay, chọn lọc khác:

Mặt phẳng tọa độ lớp 7 và cách giải các dạng bài tập

Đồ thị hàm số y = ax lớp 7 và cách giải các dạng bài tập

Công thức về tính chất của tỉ lệ thuận hay nhất

Công thức tìm hệ số tỉ lệ thuận, hệ số tỉ lệ nghịch

Cách vẽ đồ thị hàm số y = ax