Toptailieu.vn biên soạn và giới thiệu Phương pháp giải Công thức tìm hệ số tỉ lệ thuận, hệ số tỉ lệ nghịch (50 bài tập minh họa) hay, chi tiết nhất, từ cơ bản đến nâng cao giúp học sinh nắm vững kiến thức về hỗn số, từ đó học tốt môn Toán 7.

Phương pháp giải Công thức tìm hệ số tỉ lệ thuận, hệ số tỉ lệ nghịch (50 bài tập minh họa)

I. Lý thuyết

1. Tỉ lệ thuận

- Nếu hai đại lượng x; y tỉ lệ thuận với nhau thì tỉ số hai giá trị tương ứng của chúng luôn không đổi.

- Giá trị không đổi đó chính là hệ số tỉ lệ

$\frac{y_1}{x_1}=\frac{y_2}{x_2}=\frac{y_3}{x_3}=\mathrm{...}=\frac{y_n}{x_n}=k$(với k là hệ số tỉ lệ của y với x)

- Nếu đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ k (k ≠ 0) thì ta nói đại lượng x tỉ lệ thuận với đại lượng y theo hệ số tỉ lệ là $\frac{1}{k}.$

2. Tỉ lệ nghịch

- Nếu hai đại lượng x; y tỉ lệ nghịch với nhau thì tích hai giá trị của chúng luôn không đổi.

- Giá trị không đổi đó chính là hệ số tỉ lệ

$x_1.y_1=x_2.y_2=\mathrm{...}=x_n.y_n=a$(với a là hệ số tỉ lệ).

- Nếu đại lượng y tỉ lệ nghịch với đại lượng x theo hệ số tỉ lệ a (a ≠ 0) thì đại lượng x cũng tỉ lệ nghịch với đại lượng y theo hệ số tỉ lệ a.

II. Các ví dụ:

Ví dụ 1: Cho hai đại lượng x và y tỉ lệ với nhau. Biết $x_1=3;y_1=6$. Tìm hệ số tỉ lệ của y đối với x trong các trường hợp sau:

a) y tỉ lệ thuận với x.

b) y tỉ lệ nghịch với x.

Lời giải:

a) Vì y và x tỉ lệ thuận với nhau nên ta có hệ số tỉ lệ:

$k=\frac{y_1}{x_1}=\frac{6}{3}=2$

Vậy 2 là hệ số tỉ lệ khi y tỉ lệ thuận với x.

b) Vì y và x tỉ lệ nghịch với nhau nên ta có hệ số tỉ lệ:

$a=x_1.y_1=3.6=18$

Vậy 18 là hệ số tỉ lệ khi y tỉ lệ nghịch với x.

Ví dụ 2: Cho hai đại lượng x và y tỉ lệ thuận với nhau và khi x = 8 thì y = 12.

a) Tìm hệ số tỉ lệ k của y đối với x và biểu diễn y theo x.

b) Tính giá trị của y khi x = 2; x = -4.

Lời giải:

a) Vì x và y tỉ lệ thuận với nhau nên theo công thức hệ số tỉ lệ ta có:

$k=\frac{y}{x}$ với x = 8; y = 12.

$\Rightarrow k=\frac{12}{8}=\frac{3}{2}$

Do đó hệ số tỉ lệ của y đối với x là $\frac{3}{2}.$

Biểu diễn y theo x: $y=\frac{3}{2}x$.

b) Với x = 2 $\Rightarrow y=\frac{3}{2}.2=3$

Với x = -4 $\Rightarrow y=\frac{3}{2}.\left(-4\right)=-6$.

Kết luận: Với x = 2 thì y = 3; với x = -4 thì y = -6

Ví dụ 3: Cho hai đại lượng x và y tỉ lệ nghịch với nhau và khi x = 6 thì y = 15.

a) Tìm hệ số tỉ lệ của y đối với x.

b) Biểu diễn y theo x.

c) Tính giá trị của y khi x = 3; x = -45.

Lời giải:

a) Vì x và y tỉ lệ nghịch với nhau nên hệ số tỉ lệ của y đối với x là:

a = xy.

Với x = 6; y = 15$\Rightarrow a=6.15=90$

Vậy hệ số tỉ lệ của y đối với x là 90.

b) Biểu diễn y theo x là: $y=\frac{a}{x}\Rightarrow y=\frac{90}{x}$

c) Với x = 3 $\Rightarrow y=\frac{90}{3}=30$

Với x = - 45 $\Rightarrow y=\frac{90}{-45}=-2$.

Kết luận: Với x = 3 thì y = 30; với x = -45 thì y = -2

Ví dụ 4: Cứ 100kg thóc thì cho 70kg gạo. Hỏi 2 tấn thóc thì cho bao nhiêu kg gạo.

Lời giải:

Đổi 2 tấn = 2000kg

Vì số kg thóc và số kg gạo tỉ lệ thuận với nhau nên ta có:

$\frac{y_1}{x_1}=\frac{y_2}{x_2}$

Với $y_1$ = 70kg; $x_1$ = 100kg; $x_2$ = 2000kg, ta có:

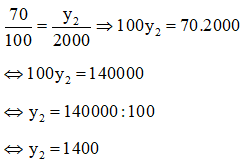
Vậy ứng với 2 tấn thóc ta thu được 1400kg gạo.

Ví dụ 5: Bạn Lan đi từ nhà đến trường với vận tốc 12km/h hết nửa giờ. Nếu Lan đi với vận tốc 10km/h thì hết bao nhiêu thời gian.

Lời giải:

Vì thời gian và vận tốc là hai đại lượng tỉ lệ nghịch với nhau nên ta có

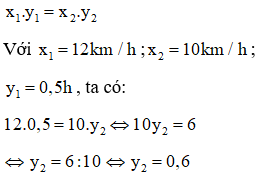
Vậy thời gian Lan đi từ nhà đến trường với vận tốc 10km/h là 0,6h.

Ví dụ 6: Biết 56 công nhân hoàn thành công việc trong 21 ngày. Nếu năng suất làm việc của mỗi công nhân là như nhau thì cần tăng thêm bao nhiêu công nhân nữa để công việc có thể xong trong 14 ngày.

Lời giải:

Vì thời gian làm việc và số công nhân làm việc tỉ lệ nghịch với nhau nên ta có:

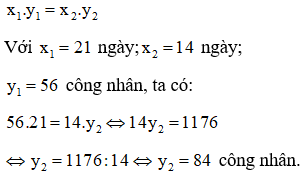
Vậy số công nhân cần tăng thêm là:

84 – 56 = 28 (công nhân)

Vậy cần tăng thêm 28 công nhân để có thể hoàn thành công việc trong 14 ngày.

Xem thêm các dạng Toán 7 hay, chọn lọc khác:

Mặt phẳng tọa độ lớp 7 và cách giải các dạng bài tập

Đồ thị hàm số y = ax lớp 7 và cách giải các dạng bài tập

Công thức về tính chất của tỉ lệ thuận hay nhất

Công thức tìm hệ số tỉ lệ thuận, hệ số tỉ lệ nghịch

Cách vẽ đồ thị hàm số y = ax