Toptailieu.vn biên soạn và giới thiệu Phương pháp giải Dãy số (HAY NHẤT 2024) gồm đầy đủ các phần: Lý thuyết, phương pháp giải, bài tập minh họa có lời giải chi tiết giúp học sinh làm tốt bài tập Toán 11 từ đó học tốt môn Toán. Mời các bạn đón xem:
Phương pháp giải Dãy số (HAY NHẤT 2024)
1. Lý thuyết
a) Định nghĩa dãy số
- Mỗi hàm số u xác định trên tập số tự nhiên được gọi là một dãy số vô hạn (gọi tắt là dãy số).
Kí hiệu:
Dạng khai triển: u1; u2; u3 ;... ; un ;...
Trong đó ta gọi: u1 là số hạng đầu, un = u(n) là số thứ n hay số hạng tổng quát của dãy số.
- Mỗi hàm số u xác định trên tập M = {1; 2; 3;... ;m} với được gọi là một dãy số hữu hạn.
Dạng khai triển của nó là u1; u2; u3 ;... ; um , trong đó u1 là số hạng đầu và um là số hạng cuối.
- Ba cách cho một dãy số:
+ Cho dãy số bằng công thức của số hạng tổng quát.
+ Cho dãy số bằng phương pháp mô tả.
+ Cho dãy số bằng phương pháp truy hồi.
b) Dãy số tăng, dãy số giảm
- Dãy số (un) được gọi là tăng nếu với mọi .
- Dãy số (un) được gọi là giảm nếu với mọi .
c) Dãy số bị chặn
- Dãy số (un) được gọi là bị chặn trên nếu tồn tại số M sao cho .
- Dãy số (un) được gọi là bị chặn dưới nếu tồn tại số m sao cho .
- Dãy số (un) được gọi là bị chặn nếu nó vừa bị chặn trên vừa bị chặn dưới, tức là tồn tại các số m, M sao cho .
2. Các dạng bài tập
Dạng 1: Tìm số hạng của dãy số
Phương pháp giải:
Bài toán 1: Cho dãy số (un): un = f(n) (trong đó f(n) là một biểu thức của n). Hãy tìm số hạng uk.
→ Thay trực tiếp n = k vào uk để tìm.
Bài toán 2: Cho dãy số (un) cho bởi (với f(un) là một biểu thức của un). Hãy tìm số hạng uk.
→ Tính lần lượt u2 ; u3 ;... ; uk bằng cách thế u1 vào u2, thế u2 vào u3, …, thế uk-1 vào uk.
Bài toán 3: Cho dãy số (un) cho bởi . Hãy tìm số hạng uk.
→ Tính lần lượt u3 ; u4;... ; uk bằng cách thế u1; u2 vào u3; thế u2;u3 vào u4; … ; thế uk -2; uk-1 vào uk.
Bài toán 4: Cho dãy số (un) cho bởi . Trong đó f({n; un)}) là kí hiệu của biểu thức un + 1 tính theo un và n. Hãy tìm số hạng uk.
→ Tính lần lượt u2 ; u3 ;... ; uk bằng cách thế {1;u1} vào u2; thế {2;u2} vào u3; … ; thế {k-1;uk-1} vào uk.
Ví dụ minh họa:
Ví dụ 1: Cho dãy số (un) được xác định bởi . Viết năm số hạng đầu của dãy.
Lời giải
Ta có năm số hạng đầu của dãy
Vậy năm số hạng đầu của dãy là: .
Ví dụ 2: Cho dãy số (un) được xác định như sau: . Tìm số hạng u11.
A. .
B. u11 = 4.
C. .
D. u11 = 5.
Lời giải
Chọn D
Ta có:
Ví dụ 3: Cho dãy số (un) được xác định như sau: . Tìm số hạng u8.
A. u8 = 3050.
B. u8 = 5003.
C. u8 = 3500.
D. u8 = 3005.
Lời giải
Chọn D
Ta có:
u3 = 2u2 + 3u1 + 5 = 12
u4 = 2u3 + 3u2 + 5 = 35
u5 = 2u4 + 3u3 + 5 = 111
u6 = 2u5 + 3u4 + 5 = 332
u7 = 2u6 + 3u5 + 5 = 1002
u8 = 2u7 + 3u6 + 5 = 3005
Dạng 2: Xét tính tăng giảm của dãy số
Phương pháp giải
Cách 1: Xét hiệu un+1 – un
- Nếu thì (un) là dãy số tăng.
- Nếu thì (un) là dãy số giảm.
Cách 2: Khi , ta xét tỉ số
- Nếu thì (un) là dãy số tăng.
- Nếu thì (un) là dãy số giảm.
Cách 3: Nếu dãy số (un) được cho bởi một hệ thức truy hồi thì ta có thể sử dụng phương pháp quy nạp để chứng minh (hoặc )
* Công thức giải nhanh một số dạng toán về dãy số
- Dãy số (un) có un = an + b tăng khi a > 0 và giảm khi a < 0
- Dãy số (un) có un = qn
+ Không tăng, không giảm khi q < 0
+ Giảm khi 0 < q < 1
+ Tăng khi q > 1
- Dãy số (un) có với điều kiện
+ Tăng khi ad – bc > 0
+ Giảm khi ad – bc < 0
- Dãy số đan dấu cũng là dãy số không tăng, không giảm
- Nếu dãy số (un) tăng hoặc giảm thì dãy số (qn. un) (với q < 0) không tăng, không giảm.
Ví dụ minh họa:
Ví dụ 1: Xét tính tăng, giảm của dãy số sau :
a) un = 3n + 6
b)
c)
Lời giải
a) Ta có
Xét hiệu
Vậy (un) là dãy số tăng.
b) Ta có
Xét hiệu
(do n là số tự nhiên)
Vậy (un) là dãy số giảm.
c) Ta có
Vậy (un) là dãy số giảm.
Ví dụ 2: Xét tính tăng, giảm của dãy số sau :
a)
b)
c)
Lời giải
a) Ta có
Xét tỉ số
Vậy (un) là dãy số tăng.
b)
Ta có:
Vậy (un) là dãy số giảm.
c)
Ta có:
Vậy (un) là dãy số tăng.
Dạng 3: Xét tính bị chặn của hàm số
Phương pháp giải:
- Cách 1: Dãy số (un) có un = f(n) là hàm số đơn giản.
Ta chứng minh trực tiếp bất đẳng thức hoặc
- Cách 2: Dự đoán và chứng minh bằng phương pháp quy nạp.
Nếu dãy số (un) được cho bởi một hệ thức truy hồi thì ta có thể sử dụng phương pháp quy nạp để chứng minh
Chú ý: Nếu dãy số (un) giảm thì bị chặn trên, dãy số (un) tăng thì bị chặn dưới
* Công thức giải nhanh một số dạng toán về dãy số bị chặn
Dãy số (un) có bị chặn
Dãy số (un) có không bị chặn
Dãy số (un) có un = qn với q > 1 bị chặn dưới
Dãy số (un) có un = an + b bị chặn dưới nếu a > 0 và bị chặn trên nếu a <0
Dãy số (un) có un = an2 + bn 8+ c bị chặn dưới nếu a > 0 và bị chặn trên nếu a < 0
Dãy số (un có un = amnm + am-1nm-1 +... + a1n + a0 bị chặn dưới nếu am > 0 và bị chặn trên nếu am < 0
Dãy số (un) có trong đó P(n) và Q(n) là các đa thức, bị chặn nếu bậc của P(n) nhỏ hơn hoặc bằng bậc của Q(n)
Dãy số (un) có trong đó P(n) và Q(n) là các đa thức, bị chặn dưới hoặc bị chặn trên nếu bậc của P(n) lớn hơn bậc của Q(n).
Ví dụ minh họa:
Ví dụ 1: Xét tính bị chặn của dãy số sau (với ):
a)
b) un = 3n – 1
c)
Lời giải
a)
Ta có
Mặt khác
Suy ra
Vậy dãy số (un) bị chặn
b) un = 3n - 1
Ta có:
Vậy (un) bị chặn dưới; không bị chặn trên.
c)
Ta có
Vậy (un) bị chặn dưới, không bị chặn trên do bậc của tử cao hơn bậc mẫu.
Ví dụ 2: Xét tính bị chặn của dãy số sau:
a)
b)
Lời giải
a)
Ta dự đoán dãy số này bị chặn (dùng máy Casio để tính một vài số hạng). Ta sẽ chứng minh bằng quy nạp:
Với n = 1 ta có (đúng)
Giả sử mệnh đề trên đúng với
Ta cần chứng minh mệnh đề trên đúng với n = k + 1
Ta có:
Theo nguyên lí quy nạp ta đã chứng minh được
Vậy (un) bị chặn.
b)
Xét
Suy ra
Vậy (un) bị chặn
3. Bài tập vận dụng
Câu 1. Cho dãy số (un) biết . Ba số hạng đầu tiên của dãy số đó lần lượt là những số nào dưới đây?
A.
B.
C.
D.
Câu 2. Cho dãy số (un) biết . Viết năm số hạng đầu của dãy số.
A.
B.
C.
D.
Câu 3. Cho dãy số (un) xác định bởi khi đó u5 bằng:
A. 317
B. 157
C. 77
D. 112
Câu 4. Cho dãy số (un) xác định bởi . Số hạng thứ tư của dãy số đó bằng
A. 0
B. 93
C. 9
D. 34
Câu 5. Cho dãy số (un) xác định bởi: . Tìm số hạng u8.
A. u8 = - 1803
B. u8 = - 5793
C. u8 = - 18147
D. u8 = - 537
Câu 6. Cho dãy số (un) biết . Mệnh đề nào sau đây đúng?
A. Dãy số tăng
B. Dãy số giảm
C. Dãy số không tăng, không giảm
D. Cả A, B, C đều sai
Câu 7. Cho dãy số (un) biết . Mệnh đề nào sau đây đúng?
A. Dãy số tăng
B. Dãy số giảm
C. Dãy số không tăng, không giảm
D.
Câu 8. Trong các dãy số (un) cho bởi số hạng tổng quát un sau, dãy số nào giảm?
A.
B. un = (- 1)n(5n - 1).
C. un = - 3n.
D.
Câu 9. Trong các dãy số (un) cho bởi số hạng tổng quát un sau, dãy số nào không tăng, không giảm?
A.
B. un = 5n + 3n.
C. un = - 3n.
D. .
Câu 10. Cho dãy số (un) biết . Mệnh đề nào sau đây đúng?
A. Dãy số tăng.
B. Dãy số giảm.
C. Dãy số không tăng, không giảm.
D. Có u10 = 2.
Câu 11. Trong các dãy số (un) sau, dãy số nào bị chặn?
A.
B. un = n + 1.
C. .
D. un = n2 + n + 1.
Câu 12. Xét tính tăng, giảm và bị chặn của dãy số (un), biết:
A. Tăng, bị chặn trên.
B. Tăng, bị chặn dưới.
C. Giảm, bị chặn.
D. Cả A, B, C đều sai.
Câu 13. Xét tính tăng, giảm và bị chặn của dãy số (un), biết:
A. Tăng, bị chặn trên.
B. Tăng, bị chặn dưới.
C. Giảm, bị chặn.
D. Cả A, B, C đều sai.
Câu 14. Xét tính bị chặn của các dãy số sau:
A. Bị chặn.
B. Không bị chặn.
C. Bị chặn trên.
D. Bị chặn dưới.
Câu 15. Xét tính tăng, giảm và bị chặn của dãy số (un), biết: .
A. Dãy số tăng, bị chặn.
B. Dãy số tăng, bị chặn dưới.
C. Dãy số giảm, bị chặn trên.
D. Cả A, B, C đều sai.
Đáp án
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
A |
B |
B |
D |
A |
A |
B |
C |
D |
B |
C |
C |
C |
A |
A |
4. Bài tập tự luyện
Bài 1: Cho dãy số (un). Khi đó số hạng thứ 5 của dãy un là
A. 10 B. 48 C. 16 D. 6
Lời giải:
Đáp án: B
Ta có u2=u1, u3=2u2, u4=3u3, u5=4u4=48. Chọn B
Bài 2: Cho dãy số un. Khi đó số hạng u3n của dãy (un) là:
Lời giải:
Đáp án: D
Bài 3: Trong các dãy số (un) cho bởi số hạng tổng quát un sau, dãy số nào bị chặn?
Lời giải:
Đáp án: A
Các dãy số n2; n; 3n dương và tăng lên vô hạn (dương vô cùng) khi n tăng lên vô hạn
nên các dãy 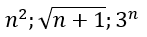
Bài 4: Trong các dãy số (un) cho bởi số hạng tổng quát un sau, dãy số nào bị chặn trên?
Lời giải:
Đáp án: C
Các dãy số n2; 2n; n+1 là các dãy tăng đến vô hạn khi n tăng lên vô hạn nên chúng không bị chặn trên (có thể dùng chức năng TABLE của MTCT để kiểm tra). Chọn C.
Bài 5: Cho dãy số (un). Dãy số (un) bị chặn trên bởi số nào dưới đây?
A. 1/3 B. 1 C.1/2 D. 0
Lời giải:
Đáp án: B
Mặt khác: un=5/7 > 1/2 > 0 nên suy ra dãy (un) bị chặn trên bởi số 1. Chọn B.
Bài 6: Trong các dãy số (un) cho bởi số hạng tổng quát un sau, dãy số nào là dãy số tăng?
Lời giải:
Đáp án: D
Vì 2n; n là các dãy dương và tăng nên 1/2n ; 1/n là các dãy giảm, do đó loại các đáp án A và B.
Xét đáp án C:
Chọn D.
Bài 7: Trong các dãy số (un) cho bởi số hạng tổng quát un sau, dãy số nào là dãy số giảm?
Lời giải:
Đáp án: C
un=sinn có thể dương hoặc âm phụ thuộc n nên đáp án A sai. Hoặc dễ thấy sinn có dấu thay đổi trên ¥ nên dãy sinn không tăng, không giảm.
nên dãy đã cho tăng nên B sai.
là dãy tăng nên suy ra un giảm.
Chọn C.
Bài 8: Cho dãy số zn = 1 + (4n – 3).2n
A. Dãy zn là dãy tăng
B. Dãy zn bị chặn dưới
C. Cả A và B đề sai
D. Cả A và B đều đúng
Lời giải:
Đáp án: B
Hướng dẫn giải. un = n2 – 4n + 7 = (n -2)2 + 3 ≥ 3
⇒ (un) bị chặn dưới bởi 3
(un) không bị chặn trên bởi vì n càng lớn thì un càng lớn
Đáp án là B
Bài 9: Cho dãy số un = n2 – 4n + 7. Kết luận nào đúng?
A. Dãy (un) bị chặn trên
B. Dãy (un) bị chặn dưới
C. Dãy (un) bị chặn
D. Các mệnh đề A,B,C đều sai
Lời giải:
Đáp án: D
Hướng dẫn giải. zn+1 = 1 + (4n+1).2n+1; zn = 1 + (4n-3).2n
⇒ zn+1-zn=2n (4n+5) > 0 ∀n ∈ N*
⇒ (zn) tăng ⇒ zn ≥ z1=3 ∀n ∈ N*
Đáp án là D
Bài 10: Cho các dãy số sau:
Khẳng định nào dưới đây là đúng?
A. (1) dãy đơn điệu tăng; (2) là dãy đơn điệu giảm; (3) là dãy đơn điệu tăng;(4) là dãy đơn điệu tăng
B. (1) dãy đơn điệu tăng; (2) là dãy đơn điệu giảm; (3) là dãy đơn điệu tăng;(4) là dãy không đơn điệu
C. (1) dãy đơn điệu tăng; (2) là dãy đơn điệu tăng; (3) là dãy không đơn điệu ;(4) là dãy không đơn điệu
D. Đáp án khác
Lời giải:
Đáp án: C
Dễ dàng có được đáp án.chọn C
Bài 11: Cho dãy số (un). Khi đó khẳng định nào dưới đây đúng?
A. un là dãy đơn điệu tăng
B. un là dãy đơn điệu giảm
C. un là dãy không đổi
D. đáp án khác
Lời giải:
Đáp án: C
Bài 12: Cho dãy số (un). Khi đó khẳng định nào dưới đây là đúng?
A. un là dãy đơn điệu tăng
B. un là dãy đơn điệu giảm
C. un là dãy không đổi
D. đáp án khác
Lời giải:
Đáp án: B
Bài 13: Xét dãy (un). Khi đó số α dương lớn nhất thoả mãn un ≥ α ∀n ≥ 1 là:
A. α =1
B. α =2
C. α =1/2
D. α =√2
Lời giải:
Đáp án: B
Bài 14: Xét dãy un với n là các số tự nhiên nhỏ hơn hoặc bằng 100, số α dương nhỏ nhất thoả mãn un ≤ α là:
A. α =10
B. α =10√2
C. α =11
D. α =20
Lời giải:
Đáp án: D
Bài 15: Cho các dãy số (un), (vn), (xn), (yn) lần lượt xác định bởi:
Trong các dãy số trên có bao nhiêu dãy bị chặn dưới
A. 1 B. 2 C. 3 D. 4
Lời giải:
Đáp án: D
Xem các Phương pháp giải bài tập hay, chi tiết khác:
Cấp số cộng và cách giải các dạng bài tập
Cấp số nhân và cách giải các dạng bài tập
Công thức tính công sai của cấp số cộng
Công thức tìm số hạng tổng quát của cấp số cộng
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.