Toptailieu.vn biên soạn và giới thiệu Công thức phép đồng dạng (50 bài tập minh họa) HAY NHẤT 2024 gồm đầy đủ các phần: Lý thuyết, phương pháp giải, bài tập minh họa có lời giải chi tiết giúp học sinh làm tốt bài tập Toán 11 từ đó học tốt môn Toán. Mời các bạn đón xem:

Công thức phép đồng dạng (50 bài tập minh họa) HAY NHẤT 2024

1. Lý thuyết

* Định nghĩa: Phép biến hình F được gọi là phép đồng dạng tỉ số k (k > 0) nếu với hai điểm M, N bất kì và ảnh M’, N’ tương ứng của chúng ta có: M’N’ = kMN.

* Tính chất:

- Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự giữa các điểm ấy.

- Biến đường thẳng thành đường thẳng; biến tia thành tia.

- Biến đoạn thẳng thành đoạn thẳng có độ dài gấp k lần độ dài đoạn thẳng ban đầu.

- Biến tam giác thành tam giác đồng dạng với tam giác đã cho với tỉ số đồng dạng k.

- Biến góc thành góc bằng nó.

- Biến đường tròn bán kính R thành đường tròn bán kính k.R.

2. Công thức

Phép biến hình F được gọi là phép đồng dạng tỉ số k (k > 0)

- Biến hai điểm M(x_M; y_M), N(x_N; y_N) thành 2 điểm tương ứng M’(x’_M; y’_M), N’(x’_N; y’_N) ta luôn có M’N’ = kMN.

- Biến đường tròn bán kính R thành đường tròn bán kính k.R.

3. Ví dụ minh họa

Ví dụ 1: Trong mặt phẳng Oxy cho đường thẳng d có phương trình $x-2\sqrt{2}=0$. Viết phương trình đường thẳng d’ là ảnh của d qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số $k=\frac{1}{2}$ và phép quay tâm O góc 45⁰.

Lời giải

* Gọi d₁ là ảnh của d qua phép vị tử tâm O , tỉ số $k=\frac{1}{2}$.

Vì d₁ song song hoặc trùng với d nên phương trình của d₁ có dạng: x + c = 0

Lấy $M\left(2\sqrt{2};0\right)\in d$ thì ảnh của M qua phép $V_{\left(O;\frac{1}{2}\right)}$ là N(x_N; y_N) thuộc d₁

Tọa độ N là:

$\left\{\begin{array}{c}{x}_N=\frac{1}{2}.2\sqrt{2}\\ y_N=\frac{1}{2}.0\end{array}\right.\iff \left\{\begin{array}{l}{x}_N=\sqrt{2}\\ y_N=0\end{array}\right.\iff N\left(\sqrt{2};0\right)$

Vậy phương trình của $d_1:x-\sqrt{2}=0$.

* Lấy hai điểm $A\left(\sqrt{2};0\right)$ và $B\left(\sqrt{2};-\sqrt{2}\right)$ thuộc d₁

Gọi ảnh của A và B qua phép quay $Q_{\left(O;45°\right)}$ A’ và B’. Khi đó đường thẳng d’ đi qua 2 điểm A’ và B’.

Tọa độ điểm A’:

$$\begin{gathered} \left\{\begin{array}{l}{x}_{A\text{'}}=\sqrt{2}\cos 45°-0.\sin 45°\\ y_{A\text{'}}=\sqrt{2}\sin 45°+0.\cos 45°\end{array}\right. \\ \iff \left\{\begin{array}{l}{x}_{A\text{'}}=1\\ y_{A\text{'}}=1\end{array}\right.\Rightarrow A\text{'}\left(1;1\right) \end{gathered}$$

Tọa độ điểm B’:

$$\begin{gathered} \left\{\begin{array}{l}{x}_{B\text{'}}=\sqrt{2}\cos 45°-\left(-\sqrt{2}\right).\sin 45°\\ y_{B\text{'}}=\sqrt{2}\sin 45°+\left(-\sqrt{2}\right).\cos 45°\end{array}\right. \\ \iff \left\{\begin{array}{l}{x}_{B\text{'}}=2\\ y_{B\text{'}}=0\end{array}\right.\Rightarrow B\text{'}\left(2;0\right) \end{gathered}$$

Phương trình đường thẳng d’ qua A’(1;1), có VTCP là $\overrightarrow{A\text{'}B\text{'}}=\left(1;-1\right)$. Suy ra VTPT là $\overrightarrow{n_{d\text{'}}}=\left(1;1\right)$.

Vậy phương trình d’: (x – 1) + (y – 1) = 0 hay x + y – 2 = 0.

Ví dụ 2: Trong mặt phẳng Oxy, cho đường tròn (C) có phương trình (x – 2)² + (y – 2)² = 4. Phép đồng dạng có được bằng cách thực hiện phép vị tự tâm I(1; 3) , tỉ số $k=\frac{1}{2}$ và phép quay tâm A(-1;1), góc quay 45⁰ biến đường tròn (C) thành đường tròn (C’) có bán kính bằng bao nhiêu?

Lời giải

Đường tròn (C) có bán kính R = 2.

Phép vị tự tâm I(1; 3) , tỉ số $k=\frac{1}{2}$ biến (C) thành (C₁) có bán kính $R_1=\frac{1}{2}R=1$.

Phép quay tâm A(-1;1) góc quay 45⁰ biến (C₁) thành (C’) có bán kính R’ = R₁ = 1.

Vậy đường tròn (C) qua phép đồng dạng như trên thành đường tròn (C’) có bán kính R’ = 1.

4. Bài tập vận dụng

Câu 1. Trong mặt phẳng tọa độ Oxy phép đồng dạng F hợp thành bởi phép vị tự tâm O(0;0) tỉ số $k=\frac{1}{2}$ và phép đối xứng trục Ox biến điểm M(4;2) thành điểm có tọa độ:

A. M’(2;-1)

B. M’(8;1)

C. M’(4;2)

D. M’(8;4)

Câu 2. Trong mặt phẳng Oxy, cho đường tròn (C) có phương trình (x – 2)² + (y – 2)² = 4. Hỏi phép đồng dạng có được bằng cách thực hiện phép vị tự tâm O , tỉ số $k=\frac{1}{2}$ và phép quay tâm O, góc quay 90⁰ sẽ biến (C) thành đường tròn nào có phương trình sau?

A. (x – 2)² + (y – 2)² = 1

B. (x – 1)² + (y – 1)² = 1         

C. (x + 2)² + (y – 1)² = 1

D. (x + 1)² + (y – 1)² = 1

Câu 3. Trong mặt phẳng Oxy, cho đường thẳng d có phương trình 2x – y = 0. Hỏi phép đồng dạng có được bằng cách thực hiện phép vị tự tâm O, tỉ số k = -2 và phép đối xứng qua trục Oy sẽ biến d thành đường thẳng nào trong các đường thẳng có phương trình sau?

A. 2x – y = 0

B. 2x + y = 0

C. 4x – y = 0

D. 2x + y – 2 = 0

Câu 4: Cho hình thoi ABCD tâm O. Gọi E, F, M, N lần lượt là trung điểm các cạnh AB, CD, BC, AD. P là phép đồng dạng biến tam giác OCF thành tam giác CAB. Tìm mệnh đề sai trong các mệnh đề sau:

A. P hợp thành bởi phép đối xứng tâm O và phép vị tự tâm A tỉ số k = 2

B. P hợp thành bởi phép đối xứng trục AC và phép vị tự tâm C tỉ số k = 2

C. P hợp thành bởi phép vị tự tâm C tỉ số k = 2 và phép đối xứng tâm O

D. P hợp thành bởi phép đối xứng trục BD và phép vị tự tâm O tỉ số k = -1

Câu 5: Cho điểm I(2;1) điểm M(-1;0) phép đồng dạng hợp thành bởi phép vị tự tâm I tỉ số k = -2 và phép đối xứng trục Ox biến M thành M’’ có tọa độ.

A.(8; -3)     

B. (-8;3)      

C. (-8;-3)      

D. (3;8)

Câu 6: Trong mặt phẳng tọa độ Oxy, phép đồng dạng F hợp thành bởi phép vị tự tâm O(0;0) tỉ số k = 3 và phép đối xứng trục Ox, biến đường thẳng d: x - y - 1 = 0 thành đường thẳng d’ có phương trình.

A. x - y + 3 = 0

B. x + y - 3 = 0

C. x + y + 3 = 0

D. x - y + 2 = 0

Câu 7: Cho hình chữ nhật ABCD tâm I. Gọi E, F, G, H lần lượt là trung điểm của AB, CD, CI, FC. Phép đồng dạng hợp thành bởi phép vị tự tâm C tỉ số k = 2 và phép đối xứng tâm I biến tứ giác IGHF thành:

A. AIFD      

B. BCFI      

C. CIEB      

D. DIEA

Câu 8: Trong mặt phẳng tọa độ Oxy phép đồng dạng F hợp thành bởi phép vị tự tâm O(0;0) tỉ số k = $\frac{1}{2}$ và phép đối xứng trục Ox biến điểm M(4;2) thành điểm có tọa độ.

A.(2;-1)      

B. (8;1)

C.(4;-2)      

D. (8;4)

5. Bài tập tự luyện 

Bài 1: Chứng minh rằng hai đa giác đều có cùng số cạnh luôn đồng dạng với nhau

Bài 2: Cho hình thang ABCD có AB song song với CD, AD = a, DC = b còn hai đỉnh A, B cố định. Gọi I là giao điểm của hai đường chéo

a. Tìm tập hợp các điểm c khi D thay đổi

b. Tìm tập hợp các điểm I khi c và D thay đổi như trong câu a

Bài 3: Cho hình chữ nhật ABCD tâm I. Gọi E, F, G, H lần lượt là trung điểm của AB, CD, CI, FC. Phép đồng dạng hợp thành bởi phép vị tự tâm C tỉ số k = 2 và phép đối xứng tâm I biến tứ giác IGHF thành:

A. AIFD

B. BCFI

C. CIEB

D. DIEA

Bài 4: Trong mặt phẳng tọa độ Oxy, phép đồng dạng F hợp thành bởi phép vị tự tâm O (0; 0) tỉ số k = 3 và phép đối xứng trục Ox, biến đường thẳng d: x – y – 1 = 0 thành đường thẳng d’ có phương trình:

A. x - y + 3 = 0

B. x + y - 3 = 0

C. x + y + 3 = 0

D. x - y + 2 = 0

Bài 5: Cho điểm I (2; 1) điểm M (-1; 0) phép đồng dạng hợp thành bởi phép vị tự tâm I tỉ số k = -2 và phép đối xứng trục Ox biến M thành M’’ có tọa độ bao nhiêu ?

Bài 6: Trong mặt phẳng tọa độ Oxy cho hai điểm A (-2; -3) và B (4; 1). Phép đồng dạng tỉ số 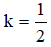 biến điểm A thành A', biến điểm B thành B'. Tính độ dài A'B'

Bài 7: Trong các khẳng định sau, khẳng định nào sai?

A. Thực hiện liên tiếp hai phép đồng dạng thì được một phép đồng dạng

B. Phép dời hình là phép đồng dạng tỉ số k = 1

C. Phép vị tự có tính chất bảo toàn khoảng cách

D. Phép vị tự không là phép dời hình

Bài 8: Cho hình vuông ABCD tâm O. M, N, P, Q lần lượt là trung điểm các cạnh AB, BC, CD, DA. Phép dời hình nào sau đây biến tam giác AMO thành tam giác CPO?

A. Phép tịnh tiến vectơ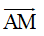 

B. Phép đối xứng trục MP

C. Phép quay tâm A góc quay 180 độ

D. Phép quay tâm O góc quay -180 độ

Bài 9: Phép biến hình có được bằng cách thực hiện liên tiếp hai phép biến hình sau đây là một phép đồng dạng tỉ số k = 3

A. Phép tịnh tiến và phép đồng nhất

B. Phép tịnh tiến và phép quay

C. Phép dời hình và phép vị tự tỉ số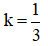 

D. Phép tịnh tiến và phép vị tự tỉ số k = -3

Bài 10: Phép đồng dạng F biến điểm M (x; y) thành M’ (x’; y’) thỏa mãn: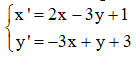 

Ảnh của điểm A (-2; 1) qua phép đồng dạng F là:

A. (6; 10)

B. (10; 6)

C. (6; -10)

D. (-6; 10)

Xem các Phương pháp giải bài tập hay, chi tiết khác: 

Đại cương về đường thẳng và mặt phẳng và cách giải bài tập

Hai đường thẳng song song trong không gian và cách giải bài tập

Đường thẳng và mặt phẳng song song và cách giải bài tập

Hai mặt phẳng song song và cách giải bài tập

Công thức Giao tuyến của ba mặt phẳng và hệ quả