Toptailieu.vn giới thiệu Giải bài tập Toán lớp 6 Bài 2: Hình có tâm đối xứng sách Chân trời sáng tạo giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán lớp 6 Tập 2. Mời các bạn đón xem:
Nội dung bài viết
Toán 6 (Chân trời sáng tạo) Bài 2: Hình có tâm đối xứng
Câu hỏi giữa bài
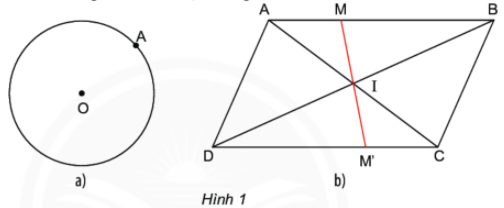
b) Cho hình bình hành ABCD, hai đường chéo AC và BD cắt nhau tại I. Đường thẳng qua I cắt AB tại M và cắt CD tại M. Đo rồi so sánh độ dài IM và IM (Hình 1b).
Phương pháp giải
a) Kẻ đường thẳng đi qua A và O, đường thẳng đó cắt đường tròn tai điểm thứ hai chính là điểm B.
b) Đo rồi so sánh độ dài IM và IM.
Lời giải
a) O là trung điểm của AB, Khi đó AB là đường kính của đường tròn.
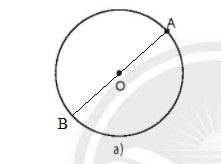
b) Độ dài IM = IM'.
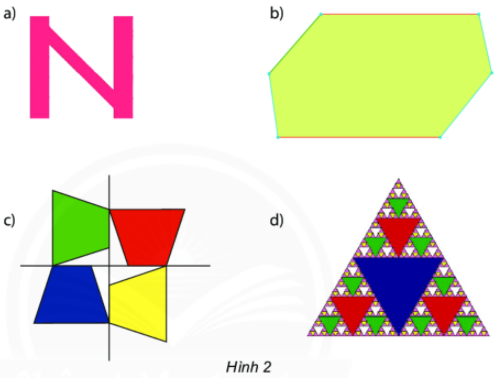
Toán lớp 6 trang 57 Thực hành 1: Tìm tâm đối xứng của mỗi hình sau (nếu có).
Phương pháp giải
Những hình có một điểm O sao cho khi quay nửa vòng quanh điểm O ta được vị trí mới của hình chồng khít với vị trí ban đầu (trước khi quay) thì được gọi là hình có tâm đối xứng và điểm O được gọi là tâm đối xứng của hình.
Lời giải
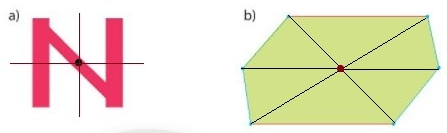
Hình a và b có tâm đối xứng:
Phương pháp giải
Những hình có một điểm O sao cho khi quay nửa vòng quanh điểm O ta được vị trí mới của hình chồng khít với vị trí ban đầu (trước khi quay) thì được gọi là hình có tâm đối xứng và điểm O được gọi là tâm đối xứng của hình.
Lời giải
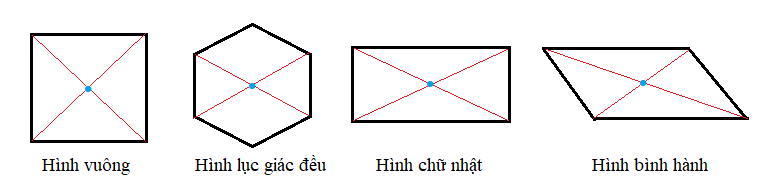
- Tâm đối xứng của hình vuông là giao điểm của hai đường chéo.
- Tâm đối xứng của hình lục giác đều là giao điểm của hai đường chéo.
- Tâm đối xứng của hình chữ nhật là giao điểm của hai đường chéo.
- Tâm đối xứng của hình bình hành là giao điểm của hai đường chéo.
Các hình không có tâm đối xứng: Tam giác đều, hình thang cân.

Phương pháp giải
Hình có tâm đối xứng O nếu điểm đối xứng với mỗi điểm thuộc hình qua điểm cũng thuộc hình
Lời giải c
Hình a có tâm đối xứng như sau:

Bài tập trang 58
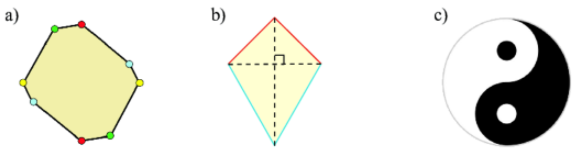
Toán lớp 6 trang 58 Bài 1: Hãy tìm tâm đối xứng của các hình sau đây (nếu có).
Phương pháp giải
Những hình có một điểm O sao cho khi quay nửa vòng quanh điểm O ta được vị trí mới của hình chồng khít với vị trí ban đầu (trước khi quay) thì được gọi là hình có tâm đối xứng và điểm O được gọi là tâm đối xứng của hình.
Lời giải
Hình a có tâm đối xứng:


Phương pháp giải
Những hình có một điểm O sao cho khi quay nửa vòng quanh điểm O ta được vị trí mới của hình chồng khít với vị trí ban đầu (trước khi quay) thì được gọi là hình có tâm đối xứng và điểm O được gọi là tâm đối xứng của hình.
Lời giải
Các hình có tâm đối xứng là:
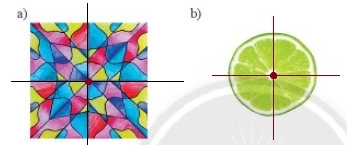

Phương pháp giải
Những hình có một điểm O sao cho khi quay nửa vòng quanh điểm O ta được vị trí mới của hình chồng khít với vị trí ban đầu (trước khi quay) thì được gọi là hình có tâm đối xứng và điểm O được gọi là tâm đối xứng của hình.
Trục đối xứng (nếu có) của một hình là đường thẳng chia hình thành hai phần, mà hai phần đó phải chồng khít lên nhau.
Lời giải
Những chữ cái có tâm đối xứng là: S, I, O, N
Những chữ cái vừa có trục đối xứng, vừa có tâm đối xứng là: I và O

Toán lớp 6 trang 58 Bài 4: Hình nào sau đây có tâm đối xứng?

Phương pháp giải
Những hình có một điểm O sao cho khi quay nửa vòng quanh điểm O ta được vị trí mới của hình chồng khít với vị trí ban đầu (trước khi quay) thì được gọi là hình có tâm đối xứng và điểm O được gọi là tâm đối xứng của hình.
Lời giải
Hình thứ nhất có tâm đối xứng.

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.