Top 10 Đề thi Giữa học kì 1 Toán 8 (Kết nối tri thức 2024) có đáp án

Giang Ngày: 23-10-2023 Lớp 8

Mua tài liệu 484

Toptailieu.vn biên soạn và giới thiệu Top 10 Đề thi Giữa học kì 1 Toán 8 (Kết nối tri thức 2024) có đáp án và hướng dẫn giải chi tiết, bám sát chương trình giáo dục phổ thông mới giúp học sinh làm quen với các dạng đề, ôn luyện để đạt kết quả cao trong bài thi Toán 8 Giữa học kì 1. Mời các bạn cùng đón xem:

Chỉ từ 150k mua trọn bộ Đề thi Toán 8 Kết nối tri thức bản word có lời giải chi tiết:

B1: Gửi phí vào tài khoản 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)

B2: Nhắn tin tới zaloVietjack Official - nhấn vào đây để thông báo và nhận giáo án.

Xem thử tài liệu tại đây:Link tài liệu

Top 10 Đề thi Giữa học kì 1 Toán 8 (Kết nối tri thức 2024) có đáp án

Phòng Giáo dục và Đào tạo ...

Đề thi Giữa kì 1 - Kết nối tri thức

Năm học ....

Môn: Toán lớp 8

Thời gian làm bài: phút

Đề thi Giữa Học kì 1 Toán 8 Kết nối tri thức - (Đề số 1)

I. Trắc nghiệm (3,0 điểm)

Câu 1. Cho các biểu thức đại số sau:

-6x²y; $x^{3} - \frac{1}{2} x y$ ; 5z³; $- \frac{4}{7} y z^{2} .5$ ; -3x + 7y; $(\sqrt{2} - 1) x$ ; $x \sqrt{y}$ .

Có bao nhiêu đơn thức trong các biểu thức đã cho ở trên?

A. 5. B. 4.

C. 3. D. 2.

Câu 2. Bậc của đa thức $x^{2} y z + \frac{1}{2} x^{3} y^{2} z + \frac{- 3}{4} x y z^{3} - 5$ là

A. 6. B. 4.

C. 3. D. 2.

Câu 3. Khẳng định nào dưới đây là sai?

A. Hai đơn thức $\frac{1}{2} x^{2} y$ và 2x²y đồng dạng với nhau.

B. Hai đơn thức 7xy³ và -9xy³ đồng dạng với nhau.

C. Hai đơn thức 5x²y² và -2x²y² đồng dạng với nhau.

D. Hai đơn thức $\frac{6}{5} x^{4} y$ và $\frac{5}{6} x y^{4}$ đồng dạng với nhau.

Câu 4. Cho đa thức A = x²y³ - 5xy²z - ^{3 $\frac{3}{7}$ x}y³z² + 4x - 5. Khẳng định nào dưới đây là đúng?

A. Đa thức A có 4 hạng tử là x²y³; -5xy²z; $- \frac{3}{7} x^{3} y^{2} z^{4}$ và 4x.

B. Đa thức A có 4 hạng tử là x²y³; 5xy²z; $\frac{3}{7} x^{3} y^{2} z^{4}$ và 4x.

C. Đa thức A có 5 hạng tử là x²y³; 5xy²z; $- \frac{3}{7} x^{3} y^{2} z^{4}$ ; 4x và -5.

D. Đa thức A có 5 hạng tử là x²y³; 5xy²z; $\frac{3}{7} x^{3} y^{2} z^{4}$ ; 4x và 5.

Câu 5. Chia đơn thức -3x³y² cho đơn thức $\frac{1}{9}$ xy ta được kết quả là

A. $- \frac{1}{3} x^{4} y^{3}$ . B. -27x²y.

C. 27x²y. D. $- \frac{1}{3} x^{4} y^{4}$ .

Câu 6. Khai triển (3x + 2)² ta được

A. 9x² - 12x + 4. B. 3x² + 12x + 4.

C. 9x² + 12x + 4. D. 3x² + 6x + 4.

Câu 7. Viết biểu thức -x³ + 3x² - 3x + 1 dưới dạng lập phương của một hiệu ta được

A. (x - 1)³. B. (x - 3)³.

C. (3 - x)³. D. (1 - x)³.

Câu 8. Biểu thức 8x³ - $\frac{1}{8}$ bằng

A. $(2 x - \frac{1}{2}) (4 x^{2} + x + \frac{1}{4})$ .

B. $(2 x - \frac{1}{2}) (4 x^{2} - x + \frac{1}{4})$ .

C. $(8 x - \frac{1}{2}) (16 x^{2} + 2 x + \frac{1}{4})$ .

D. $(2 x - \frac{1}{2}) (4 x^{2} + 2 x + \frac{1}{4})$ .

Câu 9. Thu gọn đa thức Q = x² + y² + z² + x² - y² + z² + x² + y² - z² được kết quả là

A. Q = 3x² + 3y² + 3z². B. x² + y² + z².

C. 3x² + y² + z². D. 3x² - y² - z².

Câu 10. Cho hai đa thức A = x - x² + y và B = x - y. Khẳng định nào sau đây là đúng?

A. A.B = x² + x³ + x²y - y².

B. A.B = x² - x³ + x²y - y².

C. A.B = x² - x³ - x²y - y².

D. A.B = x² - x³ - x²y + y².

Câu 11. Giá trị của biểu thức N = (2x - 2)(x² + x + 1) - (x - 1)(x + 1) tại x = 10 là

A. 1 899. B. 1 891.

C. 1 991. D. 2 001.

Câu 12. Phân tích đa thức 3x² - 6xy + 3y² - 12z² thành nhân tử ta được

A. 3(x - y - 2z)(x + y + 2z).

B. (x + y - 2z)(x - y + 2z).

C. 3(x + y - 2z)(x + y + 2z).

D. (x + y - 2z)(x + y + 2z).

II. Tự luận (7,0 điểm)

Bài 1. (2 điểm) Cho hai đa thức:

E = x⁷ - 4x³y² - 5xy và F = x⁷ + 5x³y² - 3xy - 3.

a) Tìm đa thức G sao cho G = E + F.

b) Tìm đa thức H sao cho E + H = F.

Bài 2. (1,5 điểm)

1. Tính nhanh giá trị các biểu thức sau:

a) 98²;

b) 199.201.

2. Không tính giá trị của biểu thức, hãy so sánh: M = 2021.2023 và N = 2022².

Bài 3. (1 điểm) Cho 2x = a + b + c. Chứng minh rằng:

(x - a)(x - b) + (x - b)(x - c) + (x- c)(x - a) = ab + bc + ca - x².

Bài 4. (2 điểm) Phân tích mỗi đa thức sau thành nhân tử:

a) $8 x^{3} y z + 12 x^{2} y z + 6 x y z + y z$ ;

b) $81 x^{4} (z^{2} - y^{2}) - z^{2} + y^{2}$ ;

c) $\frac{x^{3}}{8} - \frac{y^{3}}{27} + \frac{x}{2} - \frac{y}{3}$ ;

d) $x^{6} + x^{4} + x^{2} y^{2} + y^{4} - y^{6}$ .

Bài 5. (0,5 điểm) Tính giá trị của biểu thức sau:

A = $4 (3^{2} + 1) (3^{4} + 1) (3^{8} + 1) ... (3^{64} + 1)$ .

-----HẾT-----

ĐÁP ÁN ĐỀ SỐ 2

Bảng đáp án trắc nghiệm

Câu 1	B	Câu 7	D
Câu 2	A	Câu 8	A
Câu 3	D	Câu 9	C
Câu 4	C	Câu 10	B
Câu 5	B	Câu 11	A
Câu 6	C	Câu 12	C

Đáp án tự luận

Bài 1.

a) G = E + F = $2 x^{7} + x^{3} y^{2} - 8 x y + 4$ .

b) H = F - E = $9 x^{3} y^{2} + 2 x y - 10$ .

Bài 2.

a) 98² = (100 - 2)² = 100² - 2.100.2 + 2² = 10 000 - 400 + 4 = 9604.

b) 199.201 = (200 - 1).(200 + 1) = 200² - 1 = 40 000 - 1 = 39 999.

2. M = 2021.2023 = (2022 - 1).(2022 + 1) = 2022² - 1 < 2022².

Vậy M < N.

Bài 3.

VT = (x - a)(x - b) + (x - b)(x - c) + (x - c)(x - a)

= $(a b + b c + c a) + 3 x^{2} - 2 x (a + b + c)$

= $a b + b c + c a + 3 x^{2} - 2 x .2 x$

= ab + bc + ca - x² = VP.

Bài 4.

a) $8 x^{3} y z + 12 x^{2} y z + 6 x y z + y z$ = $y z {(2 x + 1)}^{3}$ .

b) $81 x^{4} (z^{2} - y^{2}) - z^{2} + y^{2}$ = $(z - y) (z + y) (9 x^{2} + 1) (3 x + 1) (3 x - 1)$ .

c) $\frac{x^{3}}{8} - \frac{y^{3}}{27} + \frac{x}{2} - \frac{y}{3}$ = $(\frac{x}{2} - \frac{y}{3}) (\frac{x^{2}}{4} + \frac{x y}{6} + \frac{y^{2}}{9} + 1)$ .

d) $x^{6} + x^{4} + x^{2} y^{2} + y^{4} - y^{6}$ = $(x^{2} + y^{2} + x y) (x^{2} + y^{2} - x y) (x^{2} - y^{2} + 1)$ .

Bài 5.

Ta có A = $(3^{2} + 1) (3^{4} + 1) (3^{8} + 1) ... (3^{64} + 1)$

Suy ra 2A = $(3 - 1) (3 + 1) (3^{2} + 1) (3^{4} + 1) (3^{8} + 1) ... (3^{64} + 1)$

Vậy A = $\frac{3^{128} - 1}{2}$ .

Phòng Giáo dục và Đào tạo ...

Đề thi Giữa kì 1 - Kết nối tri thức

Năm học ....

Môn: Toán lớp 8

Thời gian làm bài: phút

Đề thi Giữa Học kì 1 Toán 8 Kết nối tri thức - (Đề số 2)

I. Trắc nghiệm (3,0 điểm)

Câu 1. Trong các biểu thức đại số sau, biểu thức nào là đơn thức?

A. $\frac{2 x}{y}$ . B. 3x + 2y.

C. 4(x - y). D. $- \frac{2}{3} x y^{2}$ .

Câu 2. Đơn thức $25 a x^{4} y^{3} z$ (với a là hằng số) có

A. hệ số là 25, phần biến là $a x^{4} y^{3} z$ .

B. hệ số là 25, phần biến là $x^{4} y^{3} z$ .

C. hệ số là 25a, phần biến là $x^{4} y^{3} z$ .

D. hệ số là 25a, phần biến là $a x^{4} y^{3} z$ .

Câu 3. Cho các biểu thức sau:

$(5 + y^{2}) \frac{1}{x}$ ; $\frac{- 8}{9} x^{2} y (2 x - 3)$ ; $- \frac{1}{2} x^{2} y$ ; $2^{2} x^{3} + \frac{1}{3} x^{3} y^{4} - x^{4} z + x^{2}$ ; $15 + \frac{1}{z}$ .

Có bao nhiêu đa thức trong các biểu thức trên?

A. 2. B. 3.

C. 4. D. 5.

Câu 4. Bậc của đa thức $\frac{- 4}{5} x^{7} y^{2} + \frac{2}{3} x^{2} y^{5} - x y^{4}$ là

A. 9. B. 7.

C. 5. D. 3.

Câu 5. Nhân hai đơn thức $5 x^{4} y^{2} z$ và $\frac{- 1}{5} x^{3} y z^{2}$ ta được kết quả là

A. $- x^{12} y^{2} z^{2}$ . B. $- 25 x^{7} y^{3} z^{3}$ .

C. $x^{7} y^{3} z^{3}$ . D. $- x^{7} y^{3} z^{3}$ .

Câu 6. Khẳng định nào sau đây là đúng?

A. $(A - B) (A + B) = A^{2} + 2 A B + B^{2}$ .

B. $(A - B) (A + B) = A^{2} - B^{2}$ .

C. $(A - B) (A + B) = A^{2} + B^{2}$ .

D. $(A - B) (A + B) = A^{2} - 2 A B + B^{2}$ .

Câu 7. Khẳng định nào sau đây là sai?

A. ${(x + y)}^{2} = x^{2} + 2 x y + y^{2}$ .

B. ${(x + y)}^{3} = x^{3} + 3 x^{2} y + 3 x y^{2} + y^{3}$ .

C. $x^{3} - y^{3} = (x - y) (x^{2} + x y + y^{2})$ .

D. ${(x - y)}^{3} = x^{3} - y^{3}$ .

Câu 8. Khai triển biểu thức $\frac{1}{9} x^{2} - \frac{1}{64} y^{2}$ theo hằng đẳng thức ta được

A. $(\frac{x}{9} - \frac{y}{64}) (\frac{x}{9} + \frac{y}{64})$ .

B. $(\frac{x}{3} - \frac{y}{4}) (\frac{x}{3} + \frac{y}{4})$ .

C. $(\frac{x}{9} - \frac{y}{8}) (\frac{x}{9} + \frac{y}{8})$ .

D. $(\frac{x}{3} - \frac{y}{8}) (\frac{x}{3} + \frac{y}{8})$ .

Câu 9. Thu gọn đa thức $2 x^{4} y - 4 y^{5} + 5 x^{4} y - 7 y^{5} + x^{2} y^{2} - 2 x^{4} y$ ta được kết quả là

A. $5 x^{4} y - 11 y^{5} + x^{2} y^{2}$ .

B. $5 x^{4} y + 11 y^{5} + x^{2} y^{2}$ .

C. $9 x^{4} y - 11 y^{5} + x^{2} y^{2}$ .

D. $- 5 x^{4} y - 11 y^{5} + x^{2} y^{2}$ .

Câu 10. Kết quả của tích $4 a^{3} b (3 a b - b + \frac{1}{4})$ bằng

A. $- 12 a^{4} b^{2} - 4 a^{3} b^{2} + 4 a^{3} b$ .

B. $12 a^{4} b^{2} + 4 a^{3} b^{2} + a^{3} b$ .

C. $12 a^{3} b^{2} + 4 a^{3} b^{2} + 4 a^{3} b$ .

D. $12 a^{4} b^{2} - 4 a^{3} b^{2} + a^{3} b$ .

Câu 11. Để biểu thức $x^{3} + 6 x^{2} + 12 x + m$ là lập phương của một tổng thì giá trị của m là

A. 8. B. 4.

C. 6. D. 16.

Câu 12. Phân tích đa thức $5 x^{2} - 4 x + 10 x y - 8 y$ thành nhân tử ta được

A. (x + 2y)(5x - 4). B. (5x + 4)(x - 2y).

C. (5x - 4)(x - 2y). D. (5x - 2y)(x + 4y).

II. Tự luận (7,0 điểm)

Bài 1. (2 điểm)

a) Tính tổng của hai đa thức P = $x^{2} y + 2 x^{3} - x y^{2} + 5$ và Q = $x^{3} + x y^{2} - 2 x^{2} y - 6$ .

b) Tìm đa thức N biết $(2 x^{3} y - 3 x^{2} z + 1)$ + N = $- x^{3} y - 2 x^{2} z - 4$ .

Bài 2. (1,5 điểm) Rút gọn các biểu thức sau:

a) ${(3 - x y^{2})}^{2} - {(2 + x y^{2})}^{2}$ ;

b) $(x - y) (x^{2} + x y + y^{2}) - (x + y) (x^{2} - x y + y^{2})$ ;

c) ${(x - 3)}^{3} + {(2 - x)}^{3}$ .

Bài 3. (1 điểm) Chứng minh đẳng thức sau:

$(x - y) (x^{4} + x^{3} y + x^{2} y^{2} + x y^{3} + y^{4}) = x^{5} - y^{5}$ .

Bài 4. (2 điểm) Phân tích đa thức thành nhân tử rồi tính giá trị của các biểu thức sau:

a) A = $4 (x - 2) (x + 1) + {(2 x - 4)}^{2} + {(x + 1)}^{2}$ tại x = $\frac{1}{2}$ .

b) B = $x^{9} - x^{7} - x^{6} - x^{5} + x^{4} + x^{3} + x^{2} - 1$ tại x = 1.

Bài 5. (0,5 điểm) Cho đa thức A = $4 x^{9} y^{2 n} + 10 x^{10} y^{5} z^{2}$ và đơn thức B = $2 x^{3 n} y^{4}$ . Tìm số tự nhiên n để đa thức A chia hết cho đơn thức B.

Phòng Giáo dục và Đào tạo ...

Đề thi Giữa kì 1 - Kết nối tri thức

Năm học ....

Môn: Toán lớp 8

Thời gian làm bài: phút

Đề thi Giữa Học kì 1 Toán 8 Kết nối tri thức - (Đề số 3)

Phần trắc nghiệm (4 điểm)

Câu 1: Tìm hệ số trong đơn thức $- 36 a^{2} b^{2} x^{2} y^{3}$ với a,b là hằng số.

A. $- 36$	B. $- 36 a^{2} b^{2}$
C. $36 a^{2} b^{2}$	D. $- 36 a^{2}$

Câu 2: Giá trị của đa thức $4 x^{2} y - \frac{2}{3} x y^{2} + 5 x y - x$ tại $x = 2; y = \frac{1}{3}$ là

A. $\frac{176}{27}$	B. $\frac{27}{176}$
C. $\frac{17}{27}$	D. $\frac{116}{27}$

Câu 3: Chọn câu sai.

{(x + y)}^{2} = (x + y) (x + y)

x^{2} - y^{2} = (x + y) (x - y)

{(- x - y)}^{2} = {(- x)}^{2} - 2 (- x) y + y^{2}

D. $(x + y) (x + y) = y^{2} - x^{2}$ .

Câu 4: Có bao nhiêu giá trị $x$ thỏa mãn ${(2 x - 1)}^{2} - {(5 x - 5)}^{2} = 0$

A. $0$	B. $1$
C. $2$	D. $3$

Câu 5: Chọn câu đúng.

A. $8 + 12 y + 6 y^{2} + y^{3} = (8 + y^{3})$ .

B. $a^{3} + 3 a^{2} + 3 a + 1 = {(a + 1)}^{3}$ .

C. ${(2 x - y)}^{3} = 2 x^{3} - 6 x^{2} y + 6 x y - y^{3}$ .

D. ${(3 a + 1)}^{3} = 3 a^{3} + 9 a^{2} + 3 a + 1$ .

Câu 6: Tứ giác ABCD có

A B = B C, C D = D A, \hat{B} = 90^{0}; \hat{D} = 120^{0}

. Hãy chọn câu đúng nhất:

A. $\hat{A} = 85 °$ .	B. $\hat{C} = 75 °$ .
C. $\hat{A} = 75 °$ .	D. Chỉ $B$ và $C$ đúng.

Câu 7: Hình thang ABCD (AB//CD) có số đo góc D bằng $70^{0},$ số đo góc $A$ là:

A. $130^{0}$	B. $90^{0}$
C. $110^{\circ}$	D. $120^{0}$

Câu 8: Chọn câu trả lời đúng. Tứ giác nào có hai đường chéo vuông góc với nhau?

A. Hình thoi	B. Hình vuông
C. Hình chữ nhật	D. Cả A và B.

Phần tự luận (6 điểm)

Bài 1. (1,5 điểm) Cho biểu thức:

$A = 3 x (2 x - y) + (x - y) (x + y) - 7 x^{2} + y^{2}$ .

a) Thu gọn A.

b) Tính giá trị của A biết x = $\frac{- 2}{3}$ và y = 2

Bài 2. (1,5 điểm) Tìm x biết:

a) ${(x - 3)}^{2} - x^{2} = 0$

b) $x^{3} - 5 x^{2} - 9 x + 45 = 0$

c) $(5 x - 3) (2 x + 1) - {(2 x - 1)}^{2} + 4 = 0$

Bài 3. (2,5 điểm) Cho tam giác $A B C$ vuông tại $A$ , đường trung tuyến $A M$ . Gọi $H$ là điểm đối xứng với $M$ qua $A B$ , $E$ là giao điểm của $M H$ và $A B$ . Gọi $K$ là điểm đối xứng với $M$ qua $A C$ , $F$ là giao điểm của $M K$ và $A C$ .

a) Các tứ giác $A E M F$ , $A M B H$ , $A M C K$ là hình gì? Vì sao?

b) Chứng minh rằng $H$ đối xứng với $K$ qua $A$ .

c) Tam giác vuông $A B C$ cần thêm điều kiện gì thì tứ giác $A E M F$ là hình vuông?

Bài 4. (0,5 điểm) Cho a + b + c. Chứng minh $a^{3} + b^{3} + c^{3} = 3 a b c$ .

ĐÁP ÁN ĐỀ SỐ 1

Phần trắc nghiệm (4 điểm)

Câu 1: B

Câu 2: A

Câu 3: D

Câu 4: C

Câu 5: B

Câu 6: D

Câu 7: C

Câu 8: D

Câu 1:

Đơn thức $- 36 a^{2} b^{2} x^{2} y^{3}$ với a,b là hằng số có hệ số là $- 36 a^{2} b^{2} .$

Đáp án B.

Câu 2:

Thay $x = 2; y = \frac{1}{3}$ vào đa thức $4 x^{2} y - \frac{2}{3} x y^{2} + 5 x y - x$

ta được ${4.2}^{2} . \frac{1}{3} - \frac{2}{3} .2 . {(\frac{1}{3})}^{2} + 5.2. \frac{1}{3} - 2$ $= \frac{176}{27}$ .

Đáp án A.

Câu 3:

Ta có $(x + y) (x + y) = {(x + y)}^{2} = x^{2} + 2 x y + y^{2} \neq y^{2} - x^{2}$ nên câu D sai.

Đáp án D.

Câu 4:

Ta có ${(2 x - 1)}^{2} - {(5 x - 5)}^{2} = 0$

$\Leftrightarrow (2 x - 1 + 5 x - 5) (2 x - 1 - 5 x + 5) = 0$

$\Leftrightarrow (7 x - 6) (4 - 3 x) = 0 \Leftrightarrow [\begin{array}{l} 7 x - 6 = 0 \\ 4 - 3 x = 0 \end{array}$

$\Leftrightarrow [\begin{array}{l} x = \frac{6}{7} \\ x = \frac{4}{3} \end{array}$

Vậy có hai giá trị của $x$ thỏa mãn yêu cầu.

Đáp án C.

Câu 5:

Ta có $8 + 12 y + 6 y^{2} + y^{3}$

$= 2^{3} + {3.2}^{2} y + 3.2. y^{2} + y^{3}$ $= {(2 + y)}^{3} \neq (8 + y^{3})$ nên A sai.

+ Xét ${(2 x - y)}^{3}$

$= {(2 x)}^{3} - 3. {(2 x)}^{2} . y + 3.2 x . y^{2} - y^{3}$ $= 8 x^{3} - 12 x^{2} y + 6 x y - y^{3}$ $\neq 2 x^{3} - 6 x^{2} y + 6 x y - y^{3}$ nên C sai.

+ Xét ${(3 a + 1)}^{3}$

$= {(3 a)}^{3} + 3. {(3 a)}^{2} .1 + 3.3 a {.1}^{2} + 1$ $= 27 a^{3} + 27 a^{2} + 9 a + 1$ $\neq 3 a^{3} + 9 a^{2} + 3 a + 1$ nên D sai

Đáp án B.

Câu 6:

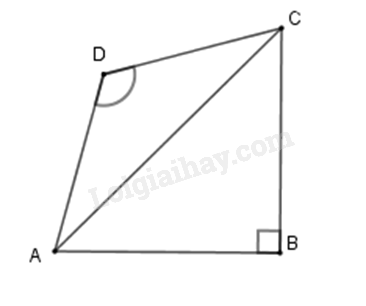
Bộ 10 đề thi giữa kì 1 Toán 8 Kết nối tri thức có đáp án năm 2023 (ảnh 1)

Xét tam giác ABC có $\hat{B} = 90^{\circ}; A B = B C \Rightarrow Δ A B C$ vuông cân

$\Rightarrow \hat{B A C} = \hat{B C A} = \frac{90^{\circ}}{2} = 45^{\circ}$

Xét tam giác ADC có $C D = D A \Rightarrow Δ A D C$ cân tại $D$ có $\hat{A D C} = 120^{\circ}$ nên $\hat{D A C} = \hat{D C A} = \frac{180^{\circ} - 120^{\circ}}{2} = 30^{\circ}$

Từ đó ta có $\hat{A} = \hat{B A D} = \hat{B A C} + \hat{C A D} = 45^{\circ} + 30^{\circ} = 75^{\circ}$

Và $\hat{C} = \hat{B C D} = \hat{B C A} + \hat{A C D} = 45^{\circ} + 30^{\circ} = 75^{\circ}$

Nên $\hat{A} = \hat{C} = 75^{\circ}$ .

Đáp án D.

Câu 7:

$\hat{A} + \hat{D} = 180^{0}$

$\begin{array}{l} \Rightarrow \hat{A} = 180^{0} - \hat{D} \\ = 180^{0} - 70^{0} \\ = 110^{0} \end{array}$

Đáp án C.

Câu 8:

Hình thoi và hình vuông đều có hai đường chéo vuông góc với nhau.

Đáp án D.

Phần tự luận.

Bài 1. (1,5 điểm)

a) $A = 3 x (2 x - y) + (x - y) (x + y) - 7 x^{2} + y^{2}$

$\begin{array}{l} = 6 x^{2} - 3 x y + x^{2} - y^{2} - 7 x^{2} + y^{2} \\ = - 3 x y \end{array}$

b) Thay x = $\frac{- 2}{3}$ và y = 2 vào A, ta được:

$A = - 3. (\frac{- 2}{3}) .2 = 1$ .

Vậy A = -3xy, giá trị của A tại x = $\frac{- 2}{3}$ và y = 2 là 1.

Bài 2. (1,5 điểm)

a) ${(x - 3)}^{2} - x^{2} = 0$

$\begin{array}{l} (x - 3 - x) (x - 3 + x) = 0 \\ - 3. (2 x - 3) = 0 \\ 2 x - 3 = 0 \\ x = \frac{3}{2} \end{array}$

Vậy $x = \frac{3}{2}$

b) $x^{3} - 5 x^{2} - 9 x + 45 = 0$

$\begin{array}{l} x^{2} (x - 5) - 9 (x - 5) = 0 \\ (x^{2} - 9) (x - 5) = 0 \\ (x - 3) (x + 3) (x - 5) = 0 \\ [\begin{array}{l} x - 3 = 0 \\ x + 3 = 0 \\ x - 5 = 0 \end{array} \\ [\begin{array}{l} x = 3 \\ x = - 3 \\ x = 5 \end{array} \end{array}$

Vậy x =3, x = -3 hoặc x = 5.

c) $(5 x - 3) (2 x + 1) - {(2 x - 1)}^{2} + 4 = 0$

$\begin{array}{l} (5 x - 3) (2 x + 1) - {(2 x - 1)}^{2} + 4 = 0 \\ (5 x - 3) (2 x + 1) - [(2 x - 1) - 4] = 0 \\ (5 x - 3) (2 x + 1) - (2 x - 1 - 2) (2 x - 1 + 2) = 0 \\ (5 x - 3) (2 x + 1) - (2 x - 3) (2 x + 1) = 0 \\ (5 x - 3 - 2 x + 3) (2 x + 1) = 0 \\ 3 x (2 x + 1) = 0 \\ [\begin{array}{l} x = 0 \\ 2 x + 1 = 0 \end{array} \\ [\begin{array}{l} x = 0 \\ x = - \frac{1}{2} \end{array} \end{array}$

Vậy x = 0 hoặc x = $- \frac{1}{2}$ .

Bài 3. (2,5 điểm)

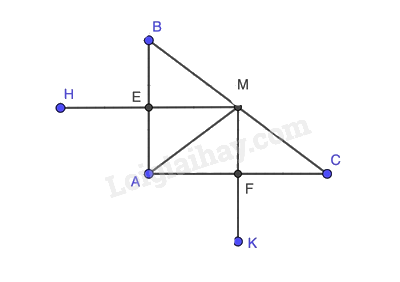
Bộ 10 đề thi giữa kì 1 Toán 8 Kết nối tri thức có đáp án năm 2023 (ảnh 2)

+ Tứ giác AEMF:

Ta có:

$\begin{array}{l} \hat{M F A} = 90^{0} (d o M F ⊥ A C) \\ \hat{F A E} = 90^{0} (g t) \\ \hat{M E A} = 90^{0} (d o M E ⊥ A B) \end{array}$

=> AEMF là hình chữ nhật.

+ Tứ giác AMBH:

Tam giác ABC vuông tại A có AM là đường trung tuyến => AM = MB = MC = $\frac{1}{2} B C$ .

=> Tam giác AMB cân tại M.

Vì ME $⊥$ AB => E là trung điểm của AB. => AE = EB.

Mà MH $⊥$ AB tại E.

=> AMBH là hình thoi.

Chứng minh tương tự, ta cũng có AMCK là hình thoi.

b) Vì AMCK là hình thoi => AK // CM, AK = CM.

Tương tự, ta cũng có AH // BM, AH = BM.

=> K, A, H thẳng hàng và AK = AH = BM = CM.

=> H đối xứng với K qua A.

c) Để AEMF là hình vuông thì AE = MF, mà AE = $\frac{1}{2}$ AB.

ME = $\frac{1}{2}$ AC.

=> AB = AC hay tam giác ABC vuông cân tại A thì AEMF là hình vuông.

Bài 4. (0,5 điểm)

Vì $a + b + c = 0$ nên ${(a + b + c)}^{3} = 0$ .

Phân tích ${(a + b + c)}^{3}$ ta được

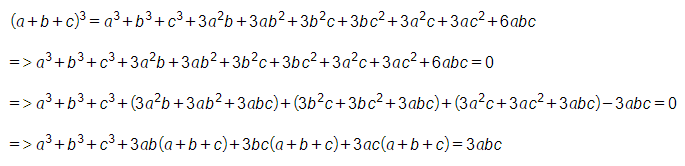
Bộ 10 đề thi giữa kì 1 Toán 8 Kết nối tri thức có đáp án năm 2023 (ảnh 3)

$D o a + b + c = 0$

$=> a^{3} + b^{3} + c^{3} = 3 a b c$ (đpcm).

Để xem trọn bộ Đề thi Toán 8 Kết nối tri thức có đáp án, Thầy/ cô vui lòng Tải xuống!

Xem thêm đề thi các môn lớp 8 bộ sách Kết nối tri thức hay, có đáp án chi tiết:

Từ khóa :

Giải bài tập Toán 8

Đánh giá

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Lớp 6

Toán 6 ( Kết nối tri thức): Luyện tập chung Mai Hương

292

Toán Lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

313

Toán Lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

342

Toán Lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

289