Cho hình lăng trụ tam giác đều ABC.A′B′C′ có cạnh đáy bằng 2a, khoảng cách từ điểm A′ đến mặt phẳng (AB′C′) bằng a√32.
a) Trong mặt phẳng (A′B′C′), kẻ A′H⊥B′C′ tại H. Khi đó B′C′⊥(AA′H).
b) d((ABC),(A′B′C′))=a.
c) Diện tích đáy của lăng trụ là a2√5.
d) Thể tích khối lăng trụ là a3√3.
 Giải bởi Vietjack
Giải bởi Vietjack
Trong mặt phẳng (AA′H) , kẻ A′K⊥AH tại K. (1)
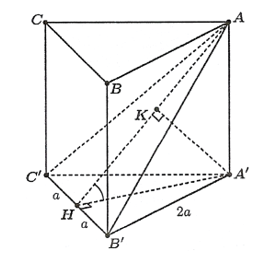
Ta có: {B′C′⊥A′HB′C′⊥AA′(doAA′⊥(A′B′C′)).
⇒B′C′⊥(AA′H)⇒A′K⊥B′C′(2).
Từ (1) và (2) suy ra A′K⊥(AB′C′) hay
d(A′,(AB′C′))=A′K=a√32.
Tam giác A′B′C′ đều có đường cao A′H=2a⋅√32=a√3.
Tam giác AA′H vuông tại A′ có đường cao A′K nên
1A′K2=1A′H2+1A′A2⇒13a24=13a2+1A′A2⇒A′A=a.
Hai mặt đáy lăng trụ song song với nhau và có khoảng cách là: d((ABC),(A′B′C′))=AA′=a.
Diện tích đáy của lăng trụ (đáy là tam giác đều) là: SΔA′B′C′=(2a)2⋅√34=a2√3.
Thể tích khối lăng trụ là: V=AA′⋅SΔA′B′C′=a⋅a2√3=a3√3.
Đáp án: a) Đúng, b) Đúng, c) Sai, d) Đúng.
50 bài tập Hình học không gian có lời giải
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, SA⊥(ABC). Tính số đo theo đơn vị độ của góc nhị diện [B,SA,C].
![Cho hình chóp \[S.ABC\] có đáy \[ABC\] là tam giác vuông cân tại \[B\], \[SA \bot \left( {ABC} \right)\]. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/01/blobid11-1736516551.png)
Cho hình chóp S.ABC có mặt bên (SAB) vuông góc với mặt đáy và tam giác SAB đều cạnh 2a. Biết tam giác ABC vuông tại C và cạnh AC=a√3.
a) SH⊥(ABC) với H là trung điểm của AB.
b) d(S,(ABC))=a√3.
c) d(C,(SAB))=a√33.
d) Thể tích của khối chóp S.ABC bằng a36.
Cho hình chóp S.ABC có SA⊥(ABC) và AB⊥BC. Số các mặt của hình chóp S.ABC là tam giác vuông là
Cho hình chóp S.ABCD có đáy là hình chữ nhật tâm O, cạnh SA vuông góc với mặt phẳng đáy. Gọi H và K lần lượt là hình chiếu của A lên SB và SD. Hỏi đường thẳng SC vuông góc với mặt phẳng nào trong các mặt phẳng sau đây?
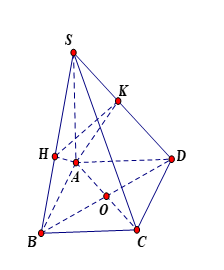
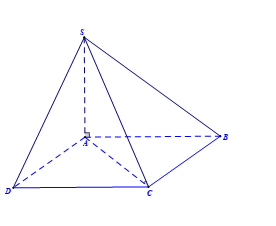
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, hai đường thẳng AC và BD cắt nhau tại O, SO⊥(ABCD), tam giác SAC là tam giác đều. Gọi M là trung điểm của cạnh AB. Tính số đo của góc nhị diện [M,SO,D].
![Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình vuông, hai đường thẳng \[AC\] và \[BD\] cắt nhau tại \[O\] (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/01/blobid13-1736516787.png)
Cho hình chóp S.ABCD có SA⊥(ABCD) và SA=a, đáy ABCD là hình vuông cạnh bằng a. Góc giữa đường thẳng SC và mặt phẳng (SAB) bằng góc nào trong các góc dưới đây?
![Cho hình chóp \[S.ABCD\] có \(SA \bot \left( {ABCD} \right)\) và \(SA = a\), đáy \[ABCD\] là hình vuông cạnh bằng (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/01/blobid10-1736516466.png)
Cho tứ diện ABCD có AB,AC,AD đôi một vuông góc với nhau. Biết rằng AB=AC=a,AD=a√3.
a) AC⊥(ABD).
d) (CD,(ABD))=30∘.
c) Góc nhị diện [A,BC,D] có số đo bằng 87,79∘.
d) Số đo của góc nhị diện [C,AB,D] bằng 90∘.
Cho hình chóp S.ABCD có SA⊥(ABCD), SA=2√6. Đáy ABCD là hình vuông cạnh bằng 2. Số đo góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng
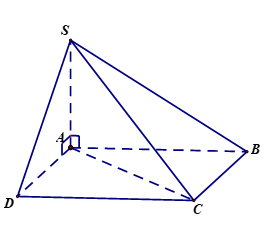
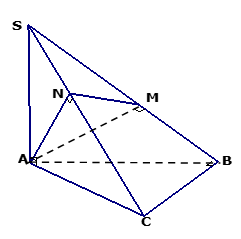
Cho tứ diện SABC có đáy ABC là tam giác vuông tại B và SA vuông góc với mặt phẳng (ABC). Gọi M,Nlần lượt là hình chiếu vuông góc của A trên cạnh SB và SC. Khẳng định nào sau đây sai?
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có AB=a,AD=b,AA′=c.
a) AB⊥(ADD′A′).
b) Khoảng cách từ điểm A đến đường thẳng BD′ bằng: √b2+c2√a2+b2+c2.
c) Gọi I,J theo thứ tự là tâm của các hình chữ nhật ADD′A′,BCC′B′. Khi đó IJ là đường vuông góc chung của hai đường thẳng AD′ và B′C.
d) Khoảng cách hai đường thẳng AD′ và B′C bằng 2a.
Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Biết ^SAD=^SCD=90∘. Số đo góc giữa hai đường thẳng SB và AC bằng bao nhiêu độ?
Nếu hai mặt phẳng cắt nhau và cùng vuông góc với mặt phẳng thứ ba thì giao tuyến của chúng có quan hệ gì với mặt phẳng thứ ba?
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.