Tìm các tiệm cận của đồ thị hàm số sau:

a) $y = 2x + 1 + \frac{1}{{x - 3}}$;

b) $y = \frac{{ - 3{x^2} + 16x - 3}}{{x - 5}}$;

c) $y = \frac{{ - 6{x^2} + 7x + 1}}{{3x + 1}}$.

Cho hàm số y = $\frac{{{x^2} + 2x - m}}{{x - 1}}$ (m là tham số).

a) Tìm m để đồ thị hàm số đã cho có hai điểm cực trị.

b) Chứng tỏ rằng khi m = 2, hàm số có hai điểm cực trị. Viết phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số này.

Chi phí để làm sạch p% lượng dầu loang từ một sự cố trên biển có thể được xấp xỉ bởi công thức

C(p) = $\frac{{2000p}}{{100 - p}}$ (tỉ đồng).

a) Tính chi phí để làm sạch 95%, 96%, 97%, 98% và 99% lượng dầu loang.

b) Tìm các tiệm cận của đồ thị hàm số C(p).

Cho hàm số y = 2x³ – 5x² – 24x – 18.

a) Hàm số có hai cực trị.

b) Hàm số đạt cực đại tại x = $- \frac{4}{3}$, giá trị cực đại là $\frac{{10}}{{27}}$.

c) Hàm số đồng biến trên khoảng (3; +∞).

d) Hàm số đồng biến trên khoảng $\left( { - \frac{4}{3};3} \right)$.

Lợi nhuận một xưởng thu được từ việc sản xuất một mặt hàng được cho bởi công thức P(q) = −q³ + 24q² + 780q – 5000 (nghìn đồng) trong đó q (kg) là khối lượng sản xuất được. Xưởng chỉ sản xuất được tối đa 50 kg sản phẩm trong một tuần.

a) Xưởng sản xuất càng nhiều thì lợi nhuận càng cao.

b) Lợi nhuận lớn nhất khi xưởng sản xuất 26 kg sản phẩm trong một tuần.

c) Sau khi sản xuất được 26 kg sản phẩm, càng sản xuất thêm thì lợi nhuận càng giảm.

d) Lợi nhuận của xưởng thấp nhất khi không sản xuất.

Cho hàm số y = 2x³ + 6x² – x + 2. Viết phương trình tiếp tuyến của đồ thị hàm số tại tâm đối xứng của nó.

Một chất điểm chuyển động theo phương ngang có tọa độ xác định bởi phương trình x(t) = −0,01t⁴ + 0,12t³ + 0,3t² + 0,5 với x tình bằng mét, t tính bằng giây, 0 ≤ t ≤ 6. Tìm thời điểm mà tốc độ của chất điểm lớn nhất.

Hàm số y = $\frac{{3x + 1}}{{x - 2}}$ có các tiệm cận là

a) x = 2.

b) x = 3.

c) y = 2.

d) y = 3.

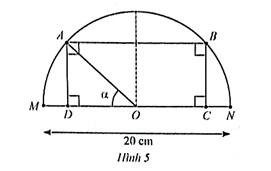
Cho điểm A di động trên nửa đường tròn tâm O đường kính MN = 20 cm, $\widehat {MOA}$ = α với 0 ≤ α ≤ π. Lấy điểm B thuộc nửa đường tròn và C, D thuộc đường kính MN được xác định sao cho ABCD là hình chữ nhật. Khi A di động từ trái sang phải, trong các khoảng nào của α thì diện tích của hình chữ nhật ABCD tăng, trong khoảng nào của α thì diện tích hình chữ nhật ABCD giảm?

Đồ thị hàm số y = $\frac{{{x^2} - 2x}}{{x + 1}}$ có hai trục đối xứng là hai đường phân giác của các góc tạo bởi hai đường thẳng:

a) x = 1 và y = x – 3.

b) x = 1 và y = −x + 3.

c) x = −1 và y = x – 3.

d) x = −1 và y = x + 3.

Cho hàm số y = (m – 1)x³ + 2(m + 1)x² – x + m – 1 (m là tham số).

a) Khảo sát và vẽ đồ thị của hàm số khi m = −1.

b) Tìm giá trị của m để tâm đối xứng của đồ thị hàm số có hoành độ x₀ = −2.

Chứng minh rằng:

a) Phương trình x³ + 5x² – 8x + 4 = 0 có duy nhất một nghiệm.

b) Phương trình −x³ + 3x² + 24x – 1 = 0 có ba nghiệm phân biệt.

Quan sát Hình 1 và trả lời các câu hỏi từ 1 đến 3.

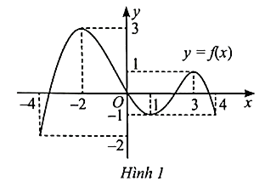
Cho hàm số y = $\frac{{{x^2} - 2x + 1}}{{x - 2}}$. Khi đó,

A. Hàm số đồng biến trên các khoảng (−∞; 1) và (3; +∞).

B. Hàm số đồng biến trên các khoảng (−1; 2) và (2; 3).

C. hàm số đồng biến trên khoảng (−∞; 2).

D. Hàm số đồng biến trên (2; +∞).

Trong một ngày, tổng chi phí để một xưởng sản xuất x (kg) thành phẩm được cho bởi hàm số C(x) = 2x³ – 30x² + 177x + 2 592 (nghìn đồng). Biết giá bán mỗi kilôgam thành phẩm là 513 nghìn đồng và công suất tối đa của xưởng 20 kg trong một ngày. Khối lượng thành phẩm xưởng nên sản xuất trong trong một ngày là bao nhiêu để lợi nhuận thu được của xưởng trong một ngày là cao nhất?

Đồ thị hàm số y = $\frac{{ - 4x + 3}}{{2x + 2}}$ có tâm đối xứng là điểm:

A. (−1; −2).

B. (−2; −1).

C. (−1; −1).

D. (−2; −2).

Cho hàm số y = x³ + 4x² – 3x + 4. Khi đó:

A. Hàm số đạt cực đại tại x = $\frac{1}{3}$, giá trị cực đại là $\frac{{94}}{{27}}$.

B. Hàm số đạt cực đại tại x = −3, giá trị cực đại là 22.

C. Hàm số đạt cực đại tại x = 0, giá trị cực đại là 4.

D. Hàm số không có cực đại.