Xét tính đơn điệu và tìm cực trị của các hàm số:
a) y = −x3 – 3x2 + 24x – 1;
b) y = x3 – 8x2 + 5x + 2;
c) y = x3 + 2x2 + 3x + 1;
d) y = −3x3 + 3x2 – x + 2.
 Giải bởi Vietjack
Giải bởi Vietjack
a) y = −x3 – 3x2 + 24x – 1
Tập xác định: D = ℝ.
Ta có: y' = −3x2 – 6x + 24 ⇔ y' = 0 ⇔ x = 2 hoặc x = −4.
Ta có bảng biến thiên như sau:
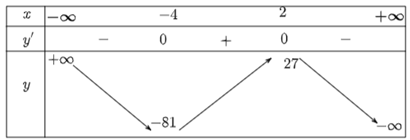
Hàm số đồng biến trên khoảng (−4; 2).
Hàm số nghịch biến trên các khoảng (−∞; −4) và (2; +∞).
Hàm số đạt cực đại tại x = 2, yCĐ = 27.
Hàm số đạt cực tiểu tại x = −4, yCT = −81.
b) y = x3 – 8x2 + 5x + 2
Tập xác định: D = ℝ.
Ta có: y' = 3x2 – 16x + 5 ⇔ y' = 0 ⇔ x = 5 hoặc x = \(\frac{1}{3}\).
Ta có bảng biến thiên:
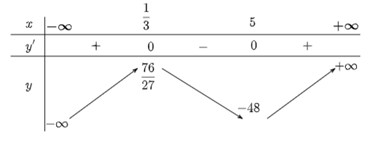
Hàm số đồng biến trên các khoảng \(\left( { - \infty ;\frac{1}{3}} \right)\) và (5; +∞).
Hàm số nghịch biến trên khoảng \(\left( {\frac{1}{3};5} \right)\).
Hàm số đạt cực đại tại x = \(\frac{1}{3}\), yCĐ = \(\frac{{76}}{{27}}\).
Hàm số đạt cực tiểu tại x = 5, yCT = −48.
c) y = x3 + 2x2 + 3x + 1
Tập xác định: D = ℝ.
Ta có: y' = 3x2 + 4x + 3 = \(3{\left( {x + \frac{2}{3}} \right)^2} + \frac{5}{3}\) > 0, với mọi x.
Do đó hàm số đồng biến trên (−∞; +∞).
Hàm số không có cực trị.
d) y = −3x3 + 3x2 – x + 2.
Tập xác định: D = ℝ.
Ta có: y' = −9x2 + 6x – 1 = −(3x – 1)2 ≤ 0, với mọi x.
Do đó, hàm số nghịch biến trên (−∞; +∞).
Hàm số không có cực trị.
Giải SBT Toán 12 Chân trời sáng tạo Bài 1. Tính đơn điệu và cực trị của hàm số có đáp án
Đồ thị đạo hàm f'(x) của hàm số y = f(x) được cho trong Hình 3.
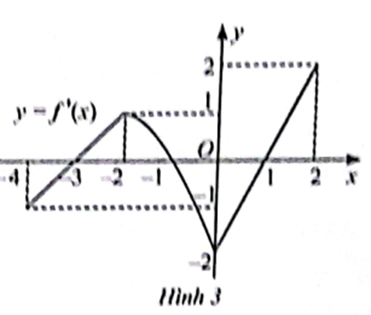
Hàm số y = f(x) đồng biến trên các khoảng
A. (−4; −2) và (−2; 2).
B. (−2; 0).
C. (−4; −3) và (−1; 1).
D. (−3; −1) và (1; 2).
Cho hàm số y = x3 – 12x + 6. Giá trị lớn nhất của hàm số trên đoạn [−3; 3] là
A. 6.
B. 15.
C. 17.
D. 22.
Cho hàm số y = \(\frac{{{x^2} - 2x + 6}}{{x + 1}}\).
A. Đồ thị hàm số có một tiệm cận xiên là y = x – 3.
B. Đồ thị hàm số có một tiệm cận xiên là y = x + 3.
C. Đồ thị hàm số có một tiệm cận xiên là y = x +1.
D. Đồ thị hàm số không có tiệm cận xiên.
Đồ thị hàm số y = \(\frac{{ - 4x + 3}}{{2x + 2}}\) có tâm đối xứng là điểm:
A. (−1; −2).
B. (−2; −1).
C. (−1; −1).
D. (−2; −2).
Cho hàm số y = 2x3 – 5x2 – 24x – 18.
a) Hàm số có hai cực trị.
b) Hàm số đạt cực đại tại x = \( - \frac{4}{3}\), giá trị cực đại là \(\frac{{10}}{{27}}\).
c) Hàm số đồng biến trên khoảng (3; +∞).
d) Hàm số đồng biến trên khoảng \(\left( { - \frac{4}{3};3} \right)\).
Hàm số y = \(\frac{{3x + 1}}{{x - 2}}\) có các tiệm cận là
a) x = 2.
b) x = 3.
c) y = 2.
d) y = 3.
Lợi nhuận một xưởng thu được từ việc sản xuất một mặt hàng được cho bởi công thức P(q) = −q3 + 24q2 + 780q – 5000 (nghìn đồng) trong đó q (kg) là khối lượng sản xuất được. Xưởng chỉ sản xuất được tối đa 50 kg sản phẩm trong một tuần.
a) Xưởng sản xuất càng nhiều thì lợi nhuận càng cao.
b) Lợi nhuận lớn nhất khi xưởng sản xuất 26 kg sản phẩm trong một tuần.
c) Sau khi sản xuất được 26 kg sản phẩm, càng sản xuất thêm thì lợi nhuận càng giảm.
d) Lợi nhuận của xưởng thấp nhất khi không sản xuất.
Đồ thị hàm số y = \(\frac{{{x^2} - 2x}}{{x + 1}}\) có hai trục đối xứng là hai đường phân giác của các góc tạo bởi hai đường thẳng:
a) x = 1 và y = x – 3.
b) x = 1 và y = −x + 3.
c) x = −1 và y = x – 3.
d) x = −1 và y = x + 3.
Giá thành của một sản phẩm trong 6 tháng đầu năm thay đổi theo công thức P(t) = 2t3 – 33t2 + 168t + 137 với P tính bằng nghìn đồng và t là số tháng tính từ đầu năm. Trong khoảng thời gian nào thì giá của sản phẩm tăng?
Tìm các khoảng đơn điệu và cực trị của các hàm số có đồ thị cho ở Hình 3.
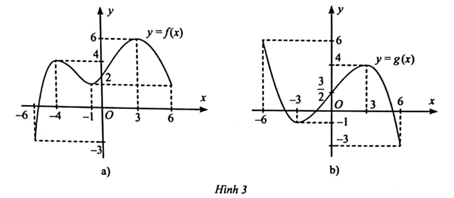
Xét tính đơn điệu và tìm cực trị của các hàm số:
a) \(y = \frac{{3x + 1}}{{x - 2}};\)
b) \(y = \frac{{2x - 5}}{{3x + 1}};\)
c) \(y = \sqrt {4 - {x^2}} \);
d) \(y = x - \ln x\).
Xét tính đơn điệu và tìm cực trị của các hàm số:
a) \(y = \frac{{{x^2} + 8}}{{x + 1}}\);
b) \(y = \frac{{{x^2} - 8x + 10}}{{x - 2}}\);
c) \(y = \frac{{ - 2{x^2} + x + 2}}{{2x - 1}}\);
d) \(y = \frac{{ - {x^2} - 6x - 25}}{{x + 3}}.\)
Tìm m để
a) Hàm số \(y = \frac{{2x + m}}{{x - 1}}\) đồng biến trên từng khoảng xác định.
b) Hàm số \(y = \frac{{ - {x^2} + 3x + m}}{{x + 2}}\) nghịch biến trên từng khoảng xác định.
Tìm các tiệm cận của đồ thị hàm số sau:
a) \(y = 2x + 1 + \frac{1}{{x - 3}}\);
b) \(y = \frac{{ - 3{x^2} + 16x - 3}}{{x - 5}}\);
c) \(y = \frac{{ - 6{x^2} + 7x + 1}}{{3x + 1}}\).
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.