Toptailieu.vn biên soạn và giới thiệu Lý thuyết Tính chất ba đường trung trực của tam giác (Cánh Diều) Toán 7 hay, ngắn gọn và bài tập tự luyện có lời giải chi tiết sẽ giúp học sinh nắm vững nội dung kiến thức từ đó dễ dàng làm các bài tập Toán 7.
Nội dung bài viết
Lý thuyết Tính chất ba đường trung trực của tam giác (Cánh Diều) Toán 7
A. Lý thuyết
1. Đường trung trực của tam giác
– Trong một tam giác, đường trung trực của mỗi cạnh được gọi là đường trung trực của tam giác đó.
Chú ý: Đường trung trực của một tam giác có thể không đi qua đỉnh nào của tam giác.
Ví dụ: Quan sát hình vẽ là chỉ ra các đường trung trực của tam giác (nếu có):
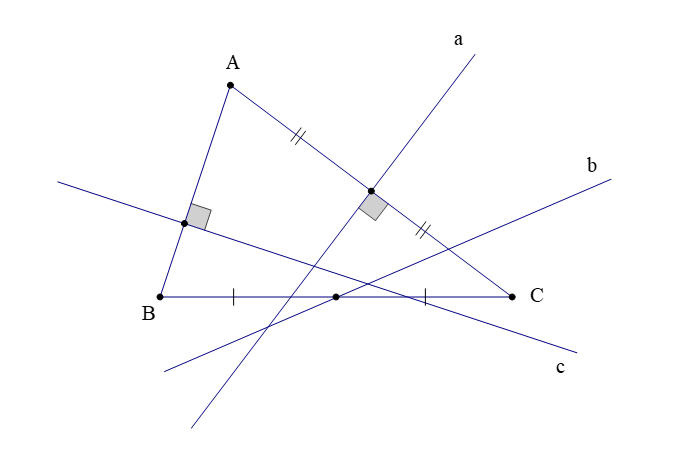
Hướng dẫn giải
Đường thẳng a vuông góc với AC tại trung điểm của cạnh đó nên đường thẳng a là trung trực của ∆ABC.
Đường thẳng b đi trung điểm của BC nhưng không vuông góc với BC tại trung điểm của cạnh đó nên đường thẳng b không là đường trung trực của ∆ABC.
Đường thẳng c ⊥ AB nhưng không vuông góc tại trung điểm của cạnh đó nên đường thẳng c không là đường trung trực của ∆ABC.
– Nhận xét: Mỗi tam giác có 3 đường trung trực.
2. Tính chất ba đường trung trực của tam giác
– Ba đường trung trực của một tam giác cùng đi qua một điểm.
Nhận xét:
+ Để xác định giao điểm ba đường trung trực của một tam giác, ta chỉ cần vẽ hai đường trung trực bất kì và xác định giao điểm của hai đường đó.
+ Giao điểm ba đường trung trực của một tam giác cách đều ba đỉnh của tam giác đó.
Do đó, trong một tam giác ba đường trung trực cùng đi qua một điểm và điểm đó cách đều ba đỉnh của tam giác.
Ví dụ: Cho ∆ABC có ba đường trung trực của AB, BC, AC cắt nhau tại O, tương ứng cắt AB, BC, CA lần lượt tại H, K, E. Chứng minh rằng: BK < OA < OC + BC.
Hướng dẫn giải
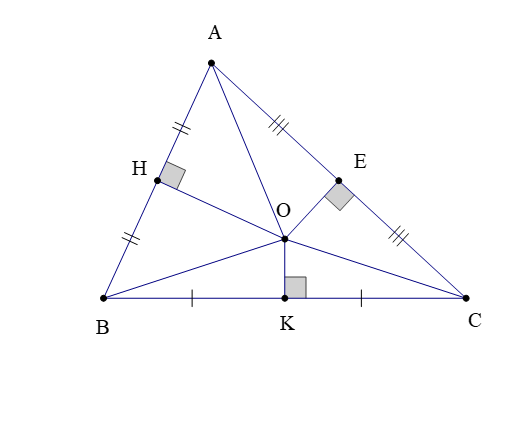
Vì O là giao điểm của ba đường trung trực trong ∆ABC nên OA = OB = OC.
Xét ∆OBK vuông tại K nên OB > BK (vì trong tam giác vuông cạnh huyền là cạnh lớn nhất). (1)
∆OBC có OB < OC + BC (bất đẳng thức trong tam giác)
Mà OA = OB
Do đó OA < OC + BC (2)
Từ (1) và (2) suy ra BK < OA < OC + BC
Vậy BK < OA < OC + BC.
B. Bài tập tự luyện
B.1 Bài tập tự luận
Bài 1. Cho ∆ABC có D là giao điểm các đường trung trực của tam giác. Kẻ DE ⊥ AC tại E; DF ⊥ AB tại F và DM ⊥ BC tại M. Chứng minh rằng DA > AB + AC +BC6.
Hướng dẫn giải
∆OBC có OB < OC + BC (bất đẳng thức trong tam giác)
Mà OA = OB
Do đó OA < OC + BC (2)
Từ (1) và (2) suy ra BK < OA < OC + BC
Vậy BK < OA < OC + BC.
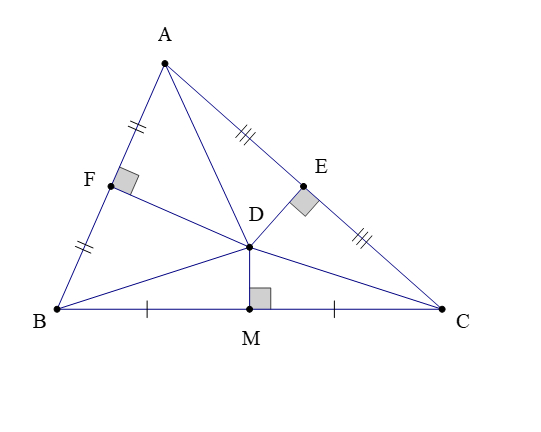
Ta có D là giao điểm các đường trung trực của ∆ABC và DE ⊥ AC tại E; DF ⊥ AB tại F và DM ⊥ BC tại M.
Suy ra DF, DM, DE lần lượt là đường trung trực của AB, BC, AC.
Do đó F, M, E lần lượt là trung điểm của AB, BC, AC
Suy ra AF=12AB, BM = 12BC, CE = 12AC
∆ADF vuông tại F nên DA > AF (vì cạnh huyền lớn nhất)
Suy ra DA > 12AB (1)
∆DBM vuông tại M nên DB > BM (vì cạnh huyền lớn nhất)
Suy ra DB > 12BC (2)
∆CDE vuông tại E nên DC > EC (vì cạnh huyền lớn nhất)
Suy ra DC > 12AC (3)
Từ (1), (2) và (3) suy ra DA + DB + DC > 12AB+12BC+12AC
Hay DA + DB + DC > 12(AB + BC+AC)
Vì D là giao điểm của các đường trung trực trong ∆ABC nên DA = DB = DC.
Do đó DA + DB + DC > 12(AB + BC+AC)
Hay DA + DA + DA > 12(AB + BC+AC)
Suy ra 3DA > 12(AB + BC+AC).
Suy ra DA > AB + BC +AC6.
Vậy DA > AB + AC +BC6.
Bài 2. Cho ∆ABC có góc A là góc tù, gọi O là giao điểm các đường trung trực của tam giác sao cho ^BOC=84°. Tính ^BAC.
Hướng dẫn giải
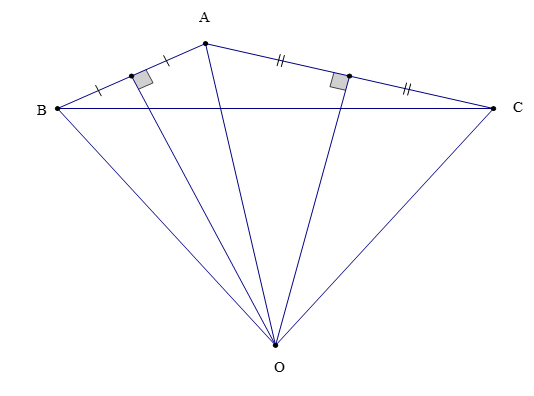
Theo bài ta có: O là giao điểm các đường trung trực của ∆ABC.
Do đó OA = OB = OC (tính chất đường trung trực trong tam giác).
• Xét ∆OAB có OA = OB nên ∆OAB cân tại O.
Suy ra ^OBA=^OAB (tính chất tam giác cân)
∆OAB có ^BOA+^OBA+^OAB=180° (tổng ba góc trong tam giác)
Suy ra ^BOA=180°−^ABO−^BAO
Mà ^OBA=^OAB (chứng minh trên)
Nên ^BOA=180°−2^BAO (1)
• Xét ∆OAC có OA = OC nên ∆OAC cân tại O.
Suy ra ^OCA=^OAC (tính chất tam giác cân).
∆OAC có ^COA+^OCA+^OAC=180°(tổng ba góc trong tam giác)
Suy ra ^COA=180°−^ACO−^CAO
Mà ^OCA=^OAC (chứng minh trên)
Suy ra ^COA=180°−2^CAO (2)
Từ (1) và (2) suy ra:
^BOA+^COA=180°−2^BAO+180°−2^CAO
Hay ^BOC=360°−2(^BAO+^CAO)
Suy ra 84°=360°−2^BAC
Suy ra 2^BAC=360°−84°=276°
Suy ra ^BAC=276°:2=138°
Vậy ^BAC=138°.
Bài 3. Cho ∆ABC vuông tại A, có ˆC=40° và đường trung trực của BC cắt AC tại M. Qua M kẻ đường thẳng song song với BC cắt AB tại N. Tính số đo các góc của ∆BMN.
Hướng dẫn giải
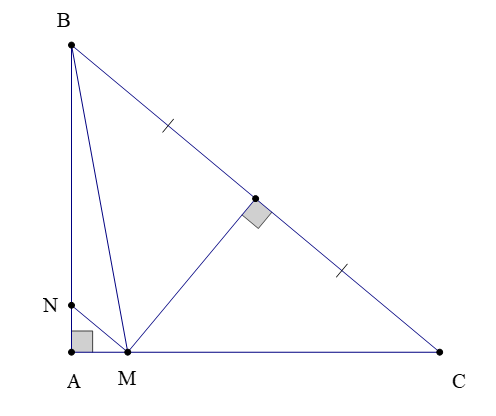
Theo bài ta có: M nằm trên đường trung trực của BC nên BM = CM.
Suy ra ∆BMC cân tại M nên ˆC=^CBM=40°
Vì MN // BC nên ^NMB=^CBM=40°(hai góc so le trong)
Xét ∆ABC vuông tại A có:
^ABC+ˆC=90°(tổng của hai góc nhọn trong tam giác vuông bằng 90°)
Suy ra ^ABC=90°−ˆC=90°−40°=50°
Ta lại có ^NBM+^MBC=^NBC=^ABC
Suy ra ^NBM=^ABC−^MBC=50°−40°=10°.
Do MN // BC nên ^MNB+^NBC=180°(hai góc trong cùng phía)
Suy ra ^MNB=180°−^NBC=180°−50°=130°.
Vậy ∆BMN có ^MNB=130°; ^NBM=10°; ^NMB=40°.
B.2 Bài tập trắc nghiệm
Câu 1. Cho ∆ABC có ˆA là góc tù. Các đường trung trực của cạnh AB và AC cắt nhau tại O và cắt BC theo thứ tự tại D và E. Khẳng định nào sau đây đúng nhất?
A. ∆ABD cân tại D;
B. ∆ACE cân tại E;
C. ∆OAB cân tại O;
D. Cả A, B, C đều đúng.
Hướng dẫn giải
Đáp án đúng là: D
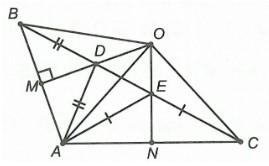
Gọi M, N lần lượt là trung điểm của AB, AC.
Vì D thuộc đường trung trực OM của cạnh AB.
Nên D cách đều A và B.
Do đó DB = DA.
Suy ra ∆ABD cân tại D.
Do đó đáp án A đúng.
Chứng minh tương tự, ta được ∆ACE cân tại E và ∆OAB cân tại O.
Do đó đáp án B, C đúng.
Vậy ta chọn đáp án D.
Câu 2. Cho ∆ABC có ˆA tù. Các đường trung trực của AB và AC cắt BC lần lượt tại D và E. Biết ^DAE=30°. Số đo ^BACbằng:
A. 95°;
B. 100°;
C. 105°;
D. 115°.
Hướng dẫn giải
Đáp án đúng là: C
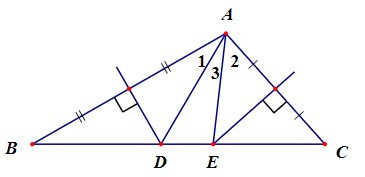
Vì điểm D nằm trên đường trung trực của AB nên DA = DB.
Suy ra ∆DAB cân tại D.
Do đó ^A1=^ABC.
Chứng minh tương tự, ta được ^A2=^ACB.
Do đó ^A1+^A2=^ABC+^ACB.
Xét tam giác ABC có: ^ABC+^BAC+^ACB=180° (tổng ba góc trong một tam giác)
Suy ra ^ABC+^ACB=180°−^BAC
Suy ra ^A1+^A2=180°−^BAC
Lại có ^A3=^BAC−(^A1+^A2).
Suy ra 30°=^BAC−(180°−^BAC)
Suy ra ^BAC−180°+^BAC=30°
Do đó 2^BAC=180°+30°=210°.
Vì vậy ^BAC=210°:2=105°.
Vậy ta chọn đáp án C.
Câu 3. Cho ∆ABC vuông tại A. Trên cạnh BC lấy điểm M bất kì. Vẽ các điểm D và E sao cho AB là đường trung trực của MD và AC là đường trung trực của ME. Khẳng định nào sau đây đúng nhất?
A. Ba điểm D, A, E thẳng hàng;
B. DE ngắn nhất khi và chỉ khi AM ngắn nhất;
C. AM ngắn nhất khi và chỉ khi M là hình chiếu của A lên cạnh BC;
D. Cả A, B, C đều đúng.
Hướng dẫn giải
Đáp án đúng là: D
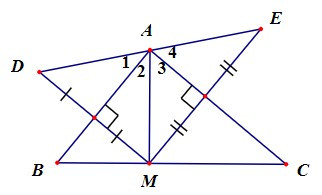
Vì AB là đường trung trực của MD.
Nên AD = AM và BD = BM (tính chất đường trung trực)
Suy ra ∆ADM cân tại A.
Xét DABD và DABM có:
AD = AM (chứng minh trên),
AB là cạnh chung,
BD = BM (chứng minh trên),
Do đó DABD = DABM (c.c.c)
Suy ra ^A1=^A2 (hai góc tương ứng)
Vì vậy ^MAD=^A1+^A2=2^A2.
Chứng minh tương tự, ta được ^A3=^A4 và ^MAE=^A3+^A4=2^A3
Ta có ^DAE=^MAD+^MAE=2(^A2+^A3)=2^BAC=2.90°=180°
Suy ra ba điểm D, A, E thẳng hàng.
Do đó đáp án A đúng.
Vì ba điểm D, A, E thẳng hàng
Nên DE = DA + AE = AM + AM = 2AM.
Suy ra DE ngắn nhất khi và chỉ khi AM ngắn nhất.
Do đó đáp án B đúng.
Vì M thuộc cạnh BC nên AM ngắn nhất khi và chỉ khi M là hình chiếu của A lên cạnh BC (quan hệ giữa đường vuông góc và đường xiên).
Do đó đáp án C đúng.
Vậy ta chọn đáp án D.
Xem thêm các bài lý thuyết Toán 7 Cánh Diều hay, chi tiết khác:
Lý thuyết Bài 10. Tính chất ba đường trung tuyến của tam giác
Lý thuyết Bài 11. Tính chất ba đường phân giác của tam giác
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.