Toptailieu.vn xin giới thiệu 30 câu trắc nghiệm Bài 5: Xác suất của biến cố (có đáp án) chọn lọc, hay nhất giúp học sinh lớp 11 ôn luyện kiến thức để đạt kết quả cao trong các bài thi môn Toán. Tài liệu gồm có các nội dung chính sau:

Mời các bạn đón xem:

30 câu trắc nghiệm Xác suất của biến cố (có đáp án) chọn lọc

Câu 1: Một lô hàng có 100 sản phẩm, biết rằng trong đó có 8 sản phẩm hỏng. Người kiểm định lấy ra ngẫu nhiên từ đó 5 sản phẩm. Tính xác suất của biến cố A: “ Người đó lấy được đúng 2 sản phẩm hỏng” ?

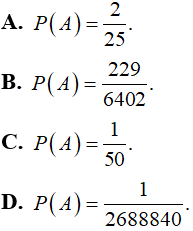
Lời giải:

Chọn đáp án B

Câu 2: Một con súc sắc không đồng chất sao cho mặt bốn chấm xuất hiện nhiều gấp 3 lần mặt khác, các mặt còn lại đồng khả năng. Tìm xác suất để xuất hiện một mặt chẵn.

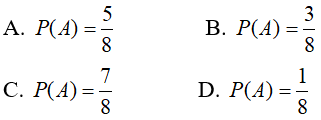
Lời giải:

Gọi Aⁱ là biến cố xuất hiện mặt i chấm (i = 1, 2, 3, 4, 5, 6)

Do cho mặt bốn chấm xuất hiện nhiều gấp 3 lần mặt khác, nên:

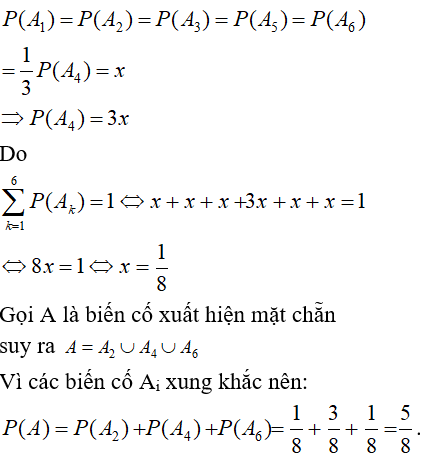
Chọn đáp án A

Câu 3: Gieo một con xúc sắc 4 lần. Tìm xác suất của biến cố

A: “ Mặt 4 chấm xuất hiện ít nhất một lần”

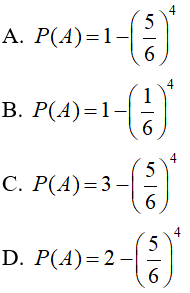
Lời giải:

Gọi A_i là biến cố “ mặt 4 chấm xuất hiện lần thứ i” với i = 1; 2; 3; 4.

Khi đó:

Chọn đáp án A

Câu 4:Gieo một con xúc sắc 4 lần. Tìm xác suất của biến cố

B: “ Mặt 3 chấm xuất hiện đúng một lần”

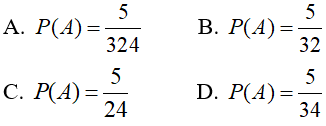
Lời giải:

Gọi B_i là biến cố “ mặt 3 chấm xuất hiện lần thứ i” với i = 1; 2; 3; 4

Khi đó:

Chọn đáp án A

Câu 5: Cả hai xạ thủ cùng bắn vào bia. Xác suất người thứ nhất bắn trúng bia là 0,8; người thứ hai bắn trúng bia là 0,7. Hãy tính xác suất để cả hai người cùng bắn trúng 

A. P(A)= 0,75

B. P(A) = 0,6

C. P(A) = 0,56

D. P(A)=0,326

Lời giải:

Chọn đáp án C

Câu 6: Cả hai xạ thủ cùng bắn vào bia. Xác suất người thứ nhất bắn trúng bia là 0,8; người thứ hai bắn trúng bia là 0,7. Hãy tính xác suất để cả hai người cùng không bắn trúng

A. P(B)=0,04

B.P(B) = 0,06

C. P(B)=0,08

D. P(B) = 0,05

Lời giải:

Chọn đáp án B

Câu 7: Cả hai xạ thủ cùng bắn vào bia. Xác suất người thứ nhất bắn trúng bia là 0,8; người thứ hai bắn trúng bia là 0,7. Hãy tính xác suất để có ít nhất một người bắn trúng.

A. P(C) =0,95

B. P(C) = 0,97

C. P(C) = 0,94

D. P(C) = 0,96

Lời giải:

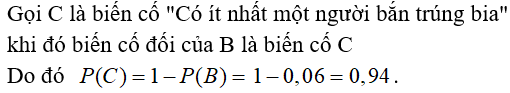
Chọn đáp án C

Câu 8: Gieo hai con súc xắc cân đối và đồng chất. Xác suất để tổng số chấm trên mặt xuất hiện của hai con súc xắc bằng 7 là:

Lời giải:

Số phần tử của không gian mẫu là:

|Ω| = 6.6 = 36.

Gọi biến cố A:      

”tổng số chấm trên mặt xuất hiện của hai con súc xắc bằng 7”.

Các kết quả thuận lợi cho A là:

A= {(1; 6); (2; 5); (3; 4); (4; 3); (5; 2); (6; 1)}.

Do đó, |Ω₆| = 6 . Vậy P(A) = 6/36 = 1/6 .

Chọn đáp án B

Câu 9: Gieo 3 con súc sắc cân đối và đồng chất. Xác suất để số chấm xuất hiện trên 3 con súc sắc đó bằng nhau:

Lời giải:

Số phần tử của không gian mẫu là:

|Ω| = 6³ = 216

A: “số chấm xuất hiện trên 3 con súc sắc đó bằng nhau”.

A = {(1,1,1); (2,2,2); (3,3,3); (4,4,4); (5,5,5); (6,6,6)}

⇒ |Ω_A| = 6

Xác suất để số chấm xuất hiện trên 3 con súc sắc đó bằng nhau là:

Chọn đáp án D

Câu 10: Có hai hộp đựng bi. Hộp I có 9 viên bi được đánh số 1, 2, 3....., 9. Lấy ngẫu nhiên mỗi hộp một viên bi. Biết rằng xác suất để lấy được viên bi mang số chẵn ở hộp II là 3/10. Xác suất để lấy được cả hai viên bi mang số chẵn là: 

Lời giải:

Chọn đáp án A

Câu 11: Một hộp chứa 5 viên bi màu trắng, 15 viên bi màu xanh và 35 viên bi màu đỏ. Lấy ngẫu nhiên từ hộp ra 7 viên bi. Xác suất để trong số 7 viên bi được lấy ra có ít nhất 1 viên bi màu đỏ là:

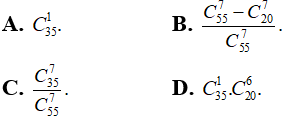
Lời giải:

Chọn đáp án B

Câu 12: Một nhóm gồm 8 nam và 7 nữ. Chọn ngẫu nhiên 5 bạn. Xác suất để trong 5 bạn được chọn có cả nam lẫn nữ mà nam nhiều hơn nữ là:

Lời giải:

Chọn đáp án B

Câu 13: Ba người cùng bắn vào 1 bia. Xác suất để người thứ nhất, thứ hai,thứ ba bắn trúng đích lần lượt là 0,8 ; 0,6; 0,5. Xác suất để có đúng 2 người bắn trúng đích bằng:

A. 0,24.

B. 0,96.

C. 0,46.

D. 0,92.

Lời giải:

Chọn đáp án C

Câu 14: Xác suất sinh con trai trong mỗi lần sinh là 0,51. Hỏi xác suất sao cho 3 lần sinh có ít nhất 1 con trai gần với số nào nhất?

A. 0,88

B. 0,23

C. 0,78

D. 0,32

Lời giải:

Chọn đáp án A

Câu 15: Hai cầu thủ sút phạt đền.Mỗi người đá 1 lần với xác suất ghi bàn tương ứng là 0,8 và 0,7. Tính xác suất để có ít nhất 1 cầu thủ ghi bàn

A. 0,42

B. 0, 94

C. 0,234

D. 0,9

Lời giải:

Chọn đáp án B

Câu 16: Một hộp đựng 40 viên bi trong đó có 20 viên bi đỏ, 10 viên bi xanh, 6 viên bi vàng,4 viên bi trắng. Lấy ngẫu nhiên 2 bi, tính xác suất biến cố A: “ lấy được 2 viên bi cùng màu”.

Lời giải:

Chọn đáp án D

Câu 17: Một cặp vợ chồng mong muốn sinh bằng đựơc sinh con trai ( sinh được con trai rồi thì không sinh nữa, chưa sinh được thì sẽ sinh nữa). Xác suất sinh được con trai trong một lần sinh là 0,51. Tìm xác suất sao cho cặp vợ chồng đó mong muốn sinh được con trai ở lần sinh thứ 2.

A. 0,24

B. 0,299

C. 0,2499

D. 0,2601

Lời giải:

Chọn đáp án C

Câu 18: Một hộp đựng 4 viên bi xanh, 3 viên bi đỏ và 2 viên bi vàng.Chọn ngẫu nhiên 2 viên bi. Tính xác suất để chọn được 2 viên bi cùng màu

Lời giải:

Chọn đáp án C

Câu 19: Một chiếc máy có hai động cơ I và II hoạt động độc lập với nhau.Xác suất để động cơ I và động cơ II chạy tốt lần lượt là 0,8 và 0,7. Hãy tính xác suất để cả hai động cơ đều chạy tốt

A. 0,56

B. 0.55

C. 0,75

D. 0,14

Lời giải:

Chọn đáp án A

Câu 20: Một chiếc máy có hai động cơ I và II hoạt động độc lập với nhau.Xác suất để động cơ I và động cơ II chạy tốt lần lượt là 0,8 và 0,7. Hãy tính xác suất để cả hai động cơ đều không chạy tốt;

A. 0,23

B. 0,56

C. 0,06

D. 0,14

Lời giải:

Chọn đáp án C

Câu 21: Một chiếc máy có hai động cơ I và II hoạt động độc lập với nhau.Xác suất để động cơ I và động cơ II chạy tốt lần lượt là 0,8 và 0,7. Hãy tính xác suất để có ít nhất một động cơ chạy tốt.

A. 0,91

B. 0,34

C. 0,12

D.0,94

Lời giải:

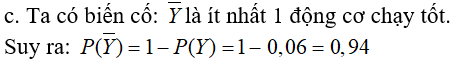
Chọn đáp án D

Câu 22: Một đội gồm 5 nam và 8 nữ. Lập một nhóm gồm 4 người hát tốp ca, tính xác suất để trong 4 người được chọn có ít nhất 3 nữ ?

Lời giải:

Chọn đáp án D

Câu 23: Có 2 hộp bút chì màu. Hộp thứ nhất có có 5 bút chì màu đỏ và 7 bút chì màu xanh. Hộp thứ hai có có 8 bút chì màu đỏ và 4 bút chì màu xanh. Chọn ngẫu nhiên mỗi hộp một cây bút chì. Xác suất để có 1 cây bút chì màu đỏ và 1 cây bút chì màu xanh là:

Lời giải:

Chọn đáp án A

Câu 24: Hai người độc lập nhau ném bóng vào rổ. Mỗi người ném vào rổ của mình một quả bóng. Biết rằng xác suất ném bóng trúng vào rổ của từng người tương ứng là 1/5 và 2/7 . Gọi A là biến cố: “Cả hai cùng ném bóng trúng vào rổ”. Khi đó, xác suất của biến cố A là bao nhiêu?

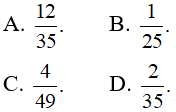
Lời giải:

Chọn đáp án D

Câu 25: Hai xạ thủ bắn mỗi người một viên đạn vào bia, biết xác suất bắn trúng vòng 10 của xạ thủ thứ nhất là 0,75 và của xạ thủ thứ hai là 0,85. Tính xác suất để có ít nhất một viên trúng vòng 10 ?

A. 0,9625

B. 0,325

C. 0, 6375

D. 0,0375

Lời giải:

Chọn đáp án A

Câu 26: Một nhóm gồm 8 nam và 7 nữ. Chọn ngẫu nhiên 5 bạn. Xác suất để trong 5 bạn được chọn có cả nam lẫn nữ mà nam nhiều hơn nữ là:

Lời giải:

Câu 27: Ba người cùng bắn vào 1 bia. Xác suất để người thứ nhất, thứ hai,thứ ba bắn trúng đích lần lượt là 0,8 ; 0,6; 0,5. Xác suất để có đúng 2 người bắn trúng đích bằng:

A. 0,24.

B. 0,96.

C. 0,46.

D. 0,92.

Lời giải:

Chọn đáp án C

Câu 28: Một lô hàng có 100 sản phẩm, biết rằng trong đó có 8 sản phẩm hỏng. Người kiểm định lấy ra ngẫu nhiên từ đó 5 sản phẩm. Tính xác suất của biến cố A: “ Người đó lấy được đúng 2 sản phẩm hỏng” ?

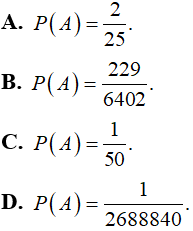
Lời giải:

Chọn đáp án B

Câu 29: Một con súc sắc không đồng chất sao cho mặt bốn chấm xuất hiện nhiều gấp 3 lần mặt khác, các mặt còn lại đồng khả năng. Tìm xác suất để xuất hiện một mặt chẵn

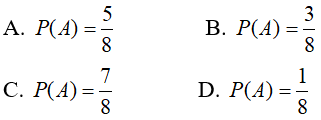
Lời giải:

Gọi Aⁱ là biến cố xuất hiện mặt i chấm (i = 1, 2, 3, 4, 5, 6)

Do cho mặt bốn chấm xuất hiện nhiều gấp 3 lần mặt khác, nên:

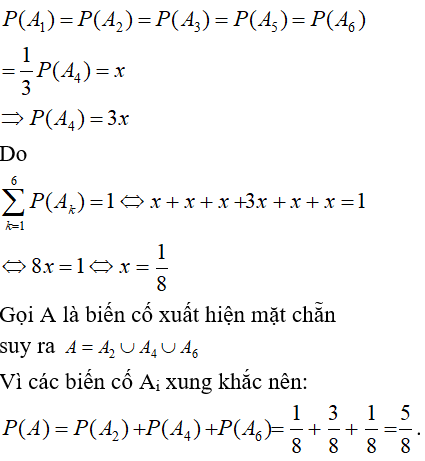
Chọn đáp án A

Câu 30: Gieo hai con súc xắc cân đối và đồng chất. Xác suất để tổng số chấm trên mặt xuất hiện của hai con súc xắc bằng 7 là:

Lời giải:

Số phần tử của không gian mẫu là:

|Ω| = 6.6 = 36.

Gọi biến cố A:

”tổng số chấm trên mặt xuất hiện của hai con súc xắc bằng 7”.

Các kết quả thuận lợi cho A là:

A= {(1; 6); (2; 5); (3; 4); (4; 3); (5; 2); (6; 1)}.

Do đó, |Ω₆| = 6 . Vậy P(A) = 6/36 = 1/6 .

Chọn đáp án B