Toptailieu.vn xin giới thiệu Lý thuyết Xác suất thực nghiệm của một biến cố trong một số trò chơi đơn giản (Cánh diều) hay, chi tiết | Lý thuyết Toán 8. Bài viết gồm phần lý thuyết trọng tâm nhất được trình bày một cách dễ hiểu, dễ nhớ bên cạnh đó là bộ câu hỏi trắc nghiệm có hướng dẫn giải chi tiết để học sinh có thể vận dụng ngay lý thuyết, nắm bài một cách hiệu quả nhất. Mời các bạn đón xem:

Lý thuyết Xác suất thực nghiệm của một biến cố trong một số trò chơi đơn giản (Cánh diều) hay, chi tiết | Lý thuyết Toán 8

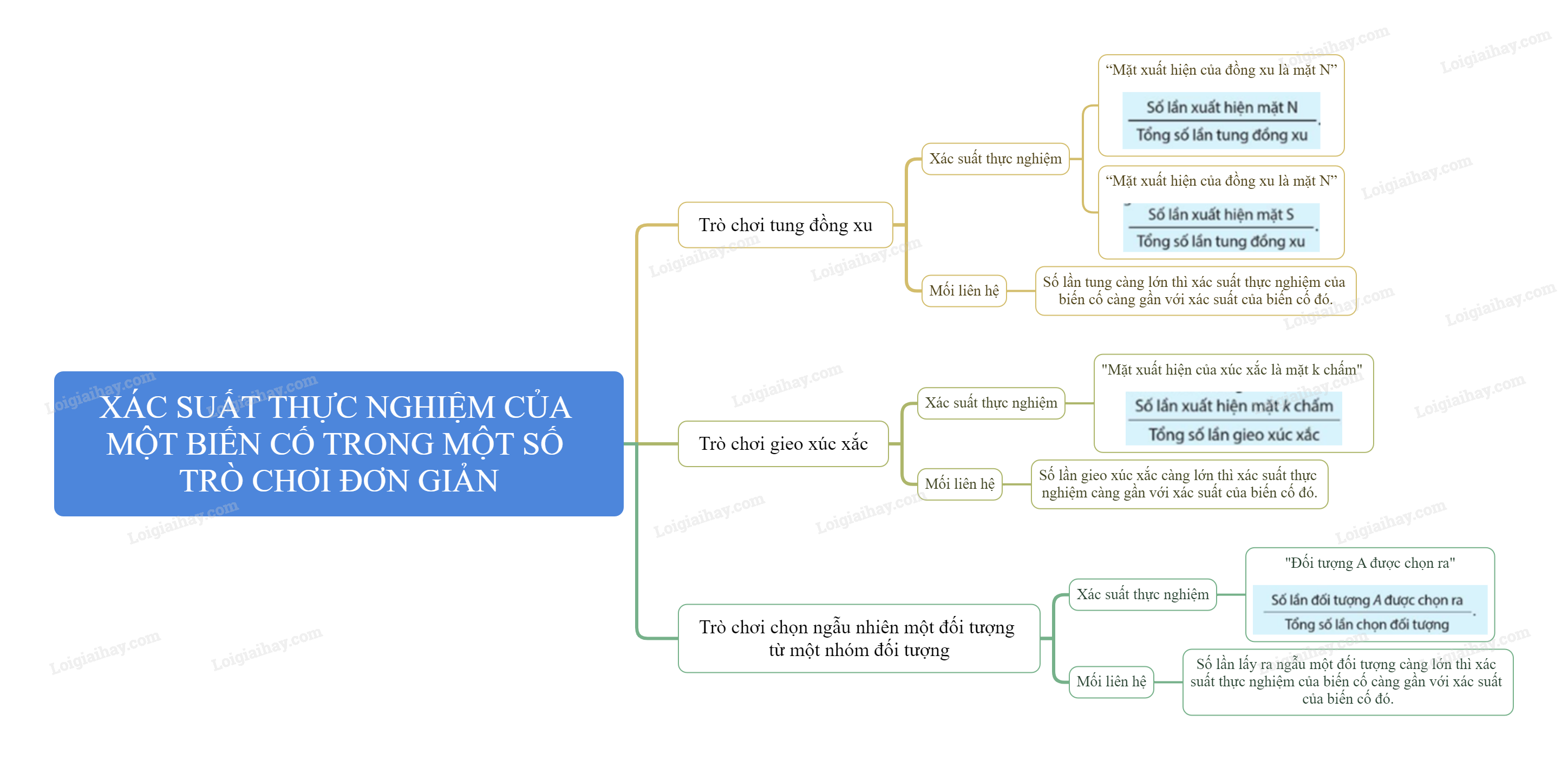
A. Lý thuyết Xác suất thực nghiệm của một biến cố trong một số trò chơi đơn giản

1. Xác suất thực nghiệm của một biến cố trong trò chơi tung đồng xu

Khái niệm:

- Xác suất thực nghiệm của biến cố “Mặt xuất hiện của đồng xu là mặt N” khi tung đồng xu nhiều lần bằng

- Xác suất thực nghiệm của biến cố “Mặt xuất hiện của đồng xu là mặt N” khi tung đồng xu nhiều lần bằng

• Mối liên hệ giữa xác suất thực nghiệm của một biến cố với xác suất của biến cố đó khi số lần thực nghiệm rất lớn

Trong trò chơi tung đồng xu, khi số lần tung ngày càng lớn thì xác suất thực nghiệm của biến cố “Mặt xuất hiện của đồng xu là mặt N” (hoặc biến cố “Mặt xuất hiện của đồng xu là mặt S”) ngày càng gần với xác suất của biến cố đó.

2. Xác suất thực nghiệm của một biến cố trong trò chơi gieo xúc xắc

• Khái niệm: Xác suất thực nghiệm của biến cố “Mặt xuất hiện của xúc xắc là mặt k chấm” ($k\in \mathbb{N},1\le k\le 6$) khi gieo xúc xắc nhiều lần bằng

• Mối liên hệ giữa xác suất thực nghiệm của một biến cố với xác suất của biến cố đó khi số lần thực nghiệm rất lớn

Trong trò chơi gieo xúc xắc, khi số lần gieo xúc xắc ngày càng lớn thì xác suất thực nghiệm của một biến cố ngày càng gần với xác suất của biến cố đó.

3. Xác suất thực nghiệm của biến cố trong trò chơi chọn ngẫu nhiên một đối tượng từ một nhóm đối tượng

• Khái niệm:

Xác suất thực nghiệm của biến cố “Đối tượng A được chọn ra” khi chọn đối tượng nhiều lần bằng

• Mối liên hệ giữa xác suất thực nghiệm của một biến cố với xác suất của biến cố đó khi số lần thực nghiệm rất lớn

Khi số lần lấy ra ngẫu một đối tượng ngày càng lớn thì xác suất thực nghiệm của biến cố “Đối tượng lấy ra là đối tượng A” ngày càng gần với xác suất của biến cố đó.

B. Bài tập Xác suất thực nghiệm của một biến cố trong một số trò chơi đơn giản

Đang cập nhật...

Xem thêm các bộ Lý thuyết Toán 8 (Cánh diều) hay, chi tiết khác:

Lý thuyết Bài 4: Xác suất của biến cố ngẫu nhiên trong một số trò chơi đơn giản

Lý thuyết Bài 1: Phương trình bậc nhất một ẩn

Lý thuyết Bài 2: Ứng dụng của phương trình bậc nhất một ẩn

Lý thuyết Bài 1: Định lí Thalès trong tam giác

Lý thuyết Bài 2: Ứng dụng của định lí Thalès trong tam giác