Toptailieu.vn giới thiệu Giải bài tập Toán lớp 7 trang 56, 57 Bài 11. Định lí và chứng minh định lí sách Kết nối tri thức giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 7 Tập 1. Mời các bạn đón xem:
Giải SGK Toán 7 Bài 11 Kết nối tri thức: Định lí và chứng minh định lí
1. Định lí. Giả thiết, kết luận của định lí
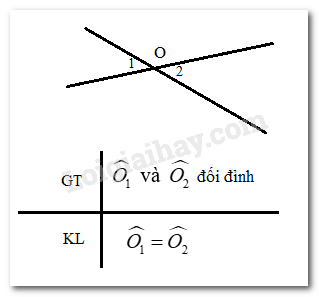
Luyện tập 1 trang 56 SGK Toán 7 Tập 1: Vẽ hình và viết giả thiết, kết luận của định lí:
“Hai góc đối đỉnh thì bằng nhau”
Phương pháp giải:
Vẽ hình
Giả thiết là điều đề bài cho
Kết luận là điều cần chứng minh
Lời giải:
2. Thế nào là chứng minh định lí?
Phương pháp giải:
Vẽ hình, viết giả thiết, kết luận rồi chứng minh
Lời giải:
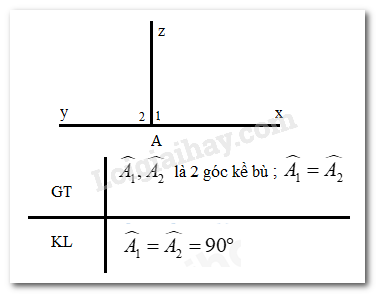
Ta có: ( 2 góc kề bù)
Mà
Vậy (đpcm)
Tranh luận trang 57 SGK Toán 7 Tập 1:
Em có ý kiến gì về hai ý kiến trên?
Phương pháp giải:
Chỉ ra ví dụ chứng tỏ khẳng định không đúng.
Lời giải:
Em thấy bạn Vuông nói đúng
Để chứng minh điều này, ta có thể chỉ ra trường hợp 2 góc bằng nhau nhưng không đối đỉnh.
Ví dụ:
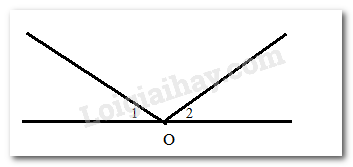
nhưng hai góc này không đối đỉnh
Bài tập:
Phương pháp giải:
Từ dấu hiệu nhận biết 2 đường thẳng song song suy ra
Lời giải
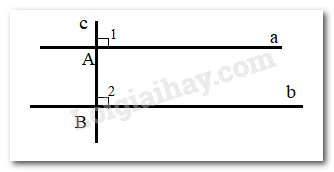
Giả sử có 2 đường thẳng phân biệt a,b cùng vuông góc với một đường thẳng c.
Ta có: , mà hai góc này ở vị trí đồng vị nên a//b (Dấu hiệu nhận biết 2 đường thẳng song song)
Như vậy, định lí trên có thể được suy ra trực tiếp từ định lí về dấu hiệu nhận biết hai đường thẳng song song.
Phương pháp giải
Sử dụng tính chất: Nếu 1 đường thẳng cắt hai đường thẳng song song thì:
Hai góc so le trong bằng nhau
Hai góc đồng vị bằng nhau
Lời giải
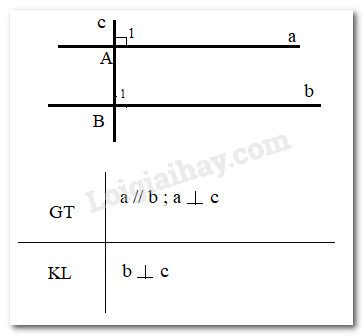
Giả sử cho 2 đường thẳng song song a và b, đường thẳng c vuông góc với a. Ta phải chứng minh c cũng vuông góc với b.
Thật vậy,
Vì a//b nên ( 2 góc đồng vị), mà nên hay (đpcm)
Trong chứng minh trên, ta đã sử dụng tính chất của hai đường thẳng song song.
(1) Nếu Ot là tia phân giác của góc xOy thì .
(2) Nếu tia Ot thỏa mãn thì Ot là tia phân giác của góc xOy.
Nếu có khẳng định không đúng, hãy nêu ví dụ cho thấy khẳng định đó không đúng.
(Gợi ý: Xét tia đối của một tia phân giác)
Phương pháp giải
Khi Om là tia phân giác của góc xOy thì
Lời giải
(1) đúng vì Ot là tia phân giác của góc xOy thì
(2) sai vì
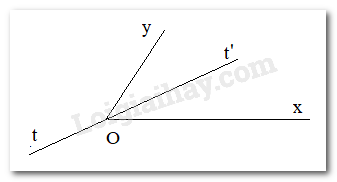
Ta có: nhưng Ot không là tia phân giác của góc xOy
Xét tia Ot’ là tia đối của tia Ot thì Ot’ là tia phân giác của góc xOy.
Chú ý:
Mỗi góc khác góc bẹt chỉ có một tia phân giác.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.
