Cho P là một điểm nằm trong góc nhọn xOy. Gọi M là điểm sao cho Ox

Giang Ngày: 15-12-2022 Lớp 7

388

Với Giải SBT Toán 7 Bài 9.20 trang 58 Tập 2 trong Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác Sách bài tập Toán lớp 7 Tập 2 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 7.

Cho P là một điểm nằm trong góc nhọn xOy. Gọi M là điểm sao cho Ox

Bài 9.20 trang 58 sách bài tập Toán 7: Cho P là một điểm nằm trong góc nhọn xOy. Gọi M là điểm sao cho Ox là đường trung trực của đoạn thẳng PM, gọi N là điểm sao cho Oy là đường trung trực của đoạn thẳng PN. Đường thẳng MN cắt Ox tại R, cắt Oy tại S.Chứng minh tia PO là tia phân giác của góc RPS.

Phương pháp giải

-O, R cùng nằm trên đường trung trực PM, chứng minh $\hat{O P R} = \hat{O M R}$ .

-O,S cùng nằm trên đường trung trực PN, chứng minh $\hat{O P S} = \hat{O N S}$ .

Lời giải

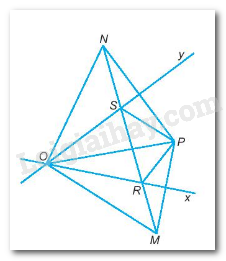
Em có biết tại sao Vuông làm nhanh thế không? (ảnh 1)

Ta có: O, R nằm trên đường trung trực của PM

$\Rightarrow O P = O M; R P = R M$ (1)

$\Rightarrow$ Tam giác OPM cân tại O, tam giác RPM cân tại R.

$\begin{array}{l} \Rightarrow {\begin{cases} \hat{O P M} = \hat{O M P} \\ \hat{R P M} = \hat{R M P} \end{cases} \\ \Rightarrow \hat{O P R} = \hat{O M R} \end{array}$

Tương tự: O, S nằm trên đường trung trực của PN

$\Rightarrow O P = O N; S P = S N$ (2)

$\Rightarrow$ Tam giác OPN cân tại O, tam giác SPN cân tại S.

$\begin{array}{l} \Rightarrow {\begin{cases} \hat{O P N} = \hat{O N P} \\ \hat{S P N} = \hat{S N P} \end{cases} \\ \Rightarrow \hat{O P S} = \hat{O N S} \end{array}$