SBT Toán 7 Kết nối tri thức Bài 34: Sự đồng quy của ba đường trung tuyến, ba đường phân giác trong một tam giác

Giang Ngày: 01-02-2023 Lớp 7

873

Toptailieu biên soạn và giới thiệu giải sách bài tập Toán 7 Bài 34: Sự đồng quy của ba đường trung tuyến, ba đường phân giác trong một tam giác sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm các bài tập từ đó nâng cao kiến thức và biết cách vận dụng phương pháp giải vào các bài tập trong SBT Toán 7 Bài 33.

Giải SBT Toán 7 Bài 34 (Kết nối tri thức): Sự đồng quy của ba đường trung tuyến, ba đường phân giác trong một tam giác

Bài 9.14 trang 55 sách bài tập Toán 7: Cho góc xAy và một điểm G trong góc đó. Lấy hai điểm M, N trên tia AG sao cho $A M = \frac{3}{2} A G; A N = 2 A M$ . Qua N kẻ đường thẳng song song với đường thẳng chứa tia Ax, nó cắt Ay tại C. Đường thẳng CM cắt Ax tại B.

a)Chứng minh hai tam giác ABM và NCM bằng nhau, từ đó suy ra AM là đường trung tuyến của tam giác ABC.

b) Chứng minh rằng G là trọng tâm của tam giác ABC vừa dựng được.

Phương pháp giải

a)Chứng minh: $Δ A B M = Δ N C M (g - c - g)$

b)Chứng minh: $A G = \frac{2}{3} A M$ .

Lời giải

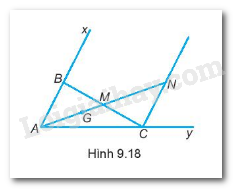
Kiểm tra lại rằng ta có phép chia hết A : B = 2x2 – 5x + 1, nghĩa là xảy ra A = B (ảnh 1)

Xét $Δ A B M$ và $Δ N C M$ có:

$\hat{M A B} = \hat{M N C}$ (2 góc so le trong NC // Ax)

$\hat{A M B} = \hat{N M C}$ (2 góc đối đỉnh)

AN = 2AM =>AM = NM

$\Rightarrow Δ A B M = Δ N C M (g - c - g)$

$\Rightarrow M B = M C$ (cạnh tương ứng)

$\Rightarrow M$ là trung điểm của BC

Vậy AM là đường trung tuyến của tam giác ABC.

Ta có: Điểm G nằm trên đường trung tuyến AM của tam giác ABC

$A M = \frac{3}{2} A G \Rightarrow A G = \frac{2}{3} A M$

Vậy G là trọng tâm tam giác ABC.

Bài 9.15 trang 55 sách bài tập Toán 7: Gọi M là trung điểm của cạnh BC của tam giác ABC và D là điểm sao cho M là trung điểm của AD. Đường thẳng qua D và trung điểm của AB cắt BC tại U, đường thẳng qua D và trung điểm của AC cắt BC tại V. Chứng minh BU = UV = VC.

Phương pháp giải

-Chứng minh: U là trọng tâm tam giác ABD.

-Chứng minh: V là trọng tâm tam giác ACD

-MB = MC

Lời giải

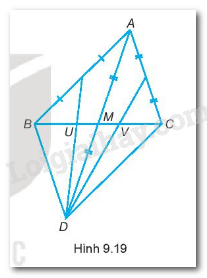
Thực hiện phép chia: a) (-x^6 + 5x^4 – 2x^3) : (0,5x^2) (ảnh 1)

-Xét tam giác ABD có:

M là trung điểm của AD, DU đi qua trung điểm AB

=>BM và DU là 2 đường trung tuyến của tam giác

Mà BM cắt DU tại U

=>U là trọng tâm tam giác ABD.

$\Rightarrow B U = 2 U M = \frac{2}{3} B M$ (1)

-Xét tam giác ACD:

M là trung điểm của AD, DV đi qua trung điểm AC

=>CM và DV là 2 đường trung tuyến của tam giác

Mà CM cắt DV tại V

=>V là trọng tâm tam giác ACD.

$\Rightarrow C V = 2 M V = \frac{2}{3} M C$ (2)

Mà M là trung điểm BC

$\Rightarrow M B = M C$

Lại có: UV = UM + MV = $\frac{1}{3} B M + \frac{1}{3} C M = \frac{1}{3} B M + \frac{1}{3} B M = \frac{2}{3} B M$ (3)

Từ (1), (2) và (3) suy ra:

BU = UV = VC.

Bài 9.16 trang 55 sách bài tập Toán 7: a)Gọi I là giao điểm của hai đường phân giác BE và CF của tam giác ABC. Đường thẳng qua I song song với BC cắt AB tại J và cắt AC tại K. Chứng minh: JK = BJ + CK.

b)Đường thẳng qua B vuông góc với BI cắt đường thẳng qua C vuông góc với CI tại điểm I’. Qua I’ kẻ đường thẳng song song với BC cắt AB tại J’, cắt AC tại K’. Chứng minh J’K’ = BJ’ + CK’.

Phương pháp giải

a)Chứng minh tam giác JIB cân tại J, tam giác IKC cân tại K

b)Áp dụng: 2 tia phân giác của 2 góc kề bù thì vuông góc với nhau.

BI vuông góc BI’ suy ra BI’ là phân giác góc ngoài tại B

Lời giải

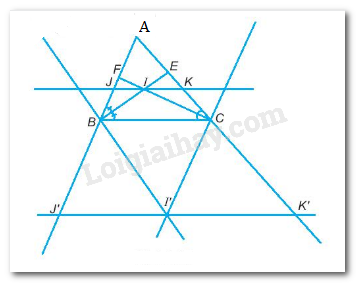
Vận dụng giải bài toán tròn tính huống mở đầu. Tìm đa thức P (ảnh 2)

Ta có: BI là phân giác góc FBC

$\Rightarrow \hat{J B I} = \hat{I B C}$

Lại có: JK // BC

$\Rightarrow \hat{J I B} = \hat{I B C}$ (2 góc so le trong)

$\Rightarrow \hat{J B I} = \hat{J I B}$

$\Rightarrow Δ J I B$ cân tại J

$\Rightarrow J I = J B$

Chứng minh tương tự: KI = KC

Ta có:

$J K = J I + I K = J B + C K$

Ta có: $B I^{'} ⊥ B I$

$\Rightarrow B I^{'}$ là tia phân giác của góc tạo bởi BC và tia đối của tia BA (phân giác góc ngoài tại B)

$\Rightarrow \hat{J^{'} B I^{'}} = \hat{I^{'} B C}$ (Tính chất tia phân giác)

Lại có: BC // J’K’

$\Rightarrow \hat{C B I^{'}} = \hat{B I^{'} J^{'}}$ (2 góc so le trong)

$\Rightarrow \hat{J^{'} B I^{'}} = \hat{B I^{'} J^{'}}$

$\Rightarrow Δ J^{'} B I^{'}$ cân tại J’

$\Rightarrow J^{'} B = J^{'} I^{'}$

Chứng minh tương tự: K’C = K’I’

Ta có:

J’K’ = J’I’ + I’K’ = BJ’ + CK’ (đpcm)

Bài 9.17 trang 55 sách bài tập Toán 7: Tam giác ABC có AD, BE là hai đường phân giác và $\hat{B A C} = 120^{0}$ . Chứng minh rằng DE là tia phân giác của góc ADC.

Phương pháp giải

- Gọi Ax là tia đối của tia AB

-Chứng minh: $\hat{B A D} = \hat{D A C} = \hat{C A x}$

- Hạ $E H ⊥ B x; E I ⊥ A D; E K ⊥ B C$

-Áp dụng điểm nằm trên tia phân giác của góc thì cách đều 2 cạnh của của góc đó.

Lời giải

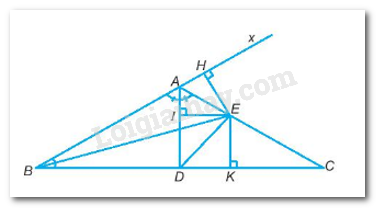
Hãy mô tả lại các bước đã thực hiện trong phép chia đa thức D cho đa thức E (ảnh 1)

Gọi Ax là tia đối của tia AB $\hat{C A x} = 180^{0} - \hat{B A C} = 180^{0} - 120^{0} = 60^{0}$ (2 góc kề bù)

AD là phân giác góc BAC

$\Rightarrow \hat{B A D} = \hat{D A C} = \frac{\hat{B A C}}{2} = \frac{120^{0}}{2} = 60^{0}$

$\Rightarrow \hat{B A D} = \hat{D A C} = \hat{C A x}$

Hạ $E H ⊥ B x; E I ⊥ A D; E K ⊥ B C$

Ta có:

EH = EK (vì BE là phân giác góc ABC)

EH = EI (vì AE là phân giác góc DAx)

$\Rightarrow E K = E I$

Vậy E nằm trên tia phân giác của góc ADC.

Bài 9.18 trang 55 sách bài tập Toán 7: Cho tam giác ABC với M là trung điểm của BC. Lấy điểm N sao cho C là trung điểm của đoạn thẳng BN. Lấy điểm P sao cho M là trung điểm của đoạn thẳng AP. Chứng minh đường thẳng AC đi qua trung điểm của PN, đường thẳng PC đi qua trung điểm của AN.

Phương pháp giải

Chứng minh CM = 2CN

Từ đó suy ra: C là trọng tâm tam giác APN

Lời giải

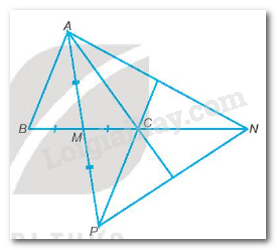
Kí hiệu dư thứ hai là G = - 6x + 10 . Đa thức này có bậc bằng 1 (ảnh 1)

Ta có:

M là trung điểm BC nên BM = CM = $\frac{1}{2} B C$

$\Rightarrow B C = 2 C M$

C là trung điểm BN nên BC = CN

$\Rightarrow C N = 2 C M$

Xét tam giác ANP có NM là đường trung tuyến

Mà: CN = 2CM (cmt)

$\Rightarrow$ C là trọng tâm tam giác ANP

$\Rightarrow$ AC, PC là hai tiếp tuyến của tam giác đó

$\Rightarrow$ AC đi qua trung điểm của PN

PC đi qua trung điểm của AN.

Xem thêm các bài giải SBT Toán lớp 7 Kết nối với tri thức hay, chi tiết khác:

Bài 33: Quan hệ giữa ba cạnh của tam giác

Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác

Ôn tập chương IX

Bài 36: Hình hộp chữ nhật và hình lập phương

Bài 37: Hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác

Từ khóa :

Giải bài tập Toán 7

Đánh giá

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Lớp 6

Toán 6 ( Kết nối tri thức): Luyện tập chung Mai Hương

203

Toán Lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

243

Toán Lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

263

Toán Lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

213