Toptailieu biên soạn và giới thiệu giải sách bài tập Toán 7 Bài 33: Quan hệ giữa ba cạnh của tam giác sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm các bài tập từ đó nâng cao kiến thức và biết cách vận dụng phương pháp giải vào các bài tập trong SBT Toán 7 Bài 33.
Nội dung bài viết
Giải SBT Toán 7 Bài 33 (Kết nối tri thức): Quan hệ giữa ba cạnh của tam giác
Phương pháp giải
-Chu vi tam giác bằng tổng ba cạnh.
-Áp dụng bất đẳng thức tam giác.
Lời giải
Gọi độ dài ba cạnh tam giác là a, b, c (cm), (a < b < c)
Cạnh lớn nhất là a = 4, b < 4, c < 4
Chu vi tam giác là: a + b + c < 4 + 4 + 4 =12
Mặt khác, theo bất đẳng thức tam giác:
b + c > a
=>a + b + c > a + a
=>a + b + c > 2a = 8
Vậy 8 < a + b + c < 12 hay chu vi tam giác đó bé hơn 12 cm và lớn hơn 8 cm.
Phương pháp giải
Áp dụng bất đẳng thức tam giác trong tam giác ABC: BC – AB < AC < BC + AB.
Lời giải
Ta có: AC = b (cm)
Áp dụng bất đẳng thức cho tam giác ABC, có:
BC – AB < AC < BC + AB
=>5 – 2 < b < 5 + 2
=>3 < b < 7
Mà b nguyên nên b = {4; 5; 6}
Bài 9.12 trang 52 sách bài tập Toán 7: Tam giác ABC có AB = 2cm, BC = 3cm. Đặt CA = b (cm)
a)Chứng minh rằng 1 < b < 5
b) Giả sử rằng với 1 < b < 5, có tam giác ABC thoả mãn AB = 2cm, BC = 3 cm, CA = b (cm). Với mỗi tam giác đó, hãy sắp xếp ba góc A, B, C theo thứ tự từ bé đến lớn.
Phương pháp giải
a)Áp dụng: BC – AB < CA < BC + AB
b)Áp dụng mối liên hệ giữa cạnh và góc trong tam giác.
Chia 3 trường hợp: 1<b≤2; 2<b≤3;3<b<5.
Lời giải
a)
Áp dụng bất đẳng thức tam giác cho tam giác ABC:
BC – AB < CA < BC + AB
=>3 – 2 < b < 3 + 2
=>1 < b < 5 (đpcm)
b)
AB = 2 cm, BC = 3 cm, AC = b
Với 1<b≤2 ⇒b≤AB<BC⇒ˆB≤ˆC<ˆA(Mối liên hệ giữa cạnh và góc trong tam giác)
Với 2<b≤3⇒AB<CA≤BC⇒ˆC<ˆB≤ˆA
Với 3<b<5⇒AB<BC<CA⇒ˆC<ˆA<ˆB
b) Cho M là một điểm bên trong tam giác ABC. Chứng minh rằng:
12(AB+BC+CA)<MA+MB+MC<AB+BC+CA
Phương pháp giải
a)
- AB + AC = AB + AN + NC = (AB + AN) + NC
-Áp dụng các bất đẳng thức tam giác: tam giác ABN, tam giác PNC.
b)
-Chứng minh: MA+MB+MC>AB+BC+CA2(áp dụng bđt tam giác ABM, MBC, MAC)
-Chứng minh:
M là điểm nằm trong tam giác ABC:
AB + AC > MB + MC
CA + CB > MA + MB
BA + BC > MA + MC
Lời giải
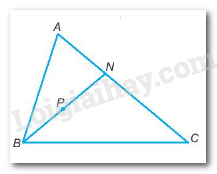
a)
P là điểm nằm trong tam giác ABC, đường thẳng BP cắt cạnh AC tại N
Ta có:
AB + AC = AB + AN + NC = (AB + AN) + NC (1)
Xét tam giác ABN: AB + AN > BN (Bất đẳng thức tam giác)
=>AB + AN > BP + PN (2)
Từ (1) và (2) suy ra: AB + AC > BP + (PN + NC) > BP + PC (Bất đẳng thức tam giác PNC)
b)
Ta có:
MA + MB > AB (bất đẳng thức trong tam giác ABM)
MB + MC > BC (bất đẳng thức trong tam giác MBC)
MC + MA > CA (bất đẳng thức trong tam giác MAC)
Cộng vế trái với vế trái, vế phải với vế phải:
2(MA + MB + MC) > AB + BC + CA
⇒MA+MB+MC>AB+BC+CA2 (1)
Mặt khác theo a)
M là điểm nằm trong tam giác ABC:
AB + AC > MB + MC
CA + CB > MA + MB
BA + BC > MA + MC
Cộng VT với VT, VP với VP:
2(AB + BC + CA) > 2(MA + MB + MC)
=>AB + BC + CA > MA + MB + MC (2)
Từ (1) và (2) suy ra:
12(AB+BC+CA)<MA+MB+MC<AB+BC+CA
Xem thêm các bài giải SBT Toán lớp 7 Kết nối với tri thức hay, chi tiết khác:
Bài 32: Quan hệ giữa đường vuông góc và đường xiên
Bài 34: Sự đồng quy của ba đường trung tuyến, ba đường phân giác trong một tam
Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.