Toptailieu biên soạn và giới thiệu giải sách bài tập Toán 7 Bài 32: Quan hệ giữa đường vuông góc và đường xiên sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm các bài tập từ đó nâng cao kiến thức và biết cách vận dụng phương pháp giải vào các bài tập trong SBT Toán 7 Bài 32.
Nội dung bài viết
Giải SBT Toán 7 Bài 32 (Kết nối tri thức): Quan hệ giữa đường vuông góc và đường xiên
Bài 9.5 trang 50 sách bài tập Toán 7: Cho 2 đường thẳng song song c và d. Chứng minh rằng khoảng cách từ mọi điểm thuộc c đến đường thẳng d bằng nhau và bằng khoảng cách từ mọi điểm thuộc đường thẳng d đến đường thẳng c (khoảng cách đó được gọi là khoảng cách giữa hai đường thẳng song song c và d).
Phương pháp giải
-Lấy M, M’ thuộc c (M khác M’), kẻ MH, M’H’ vuông góc với d.
-Chứng minh: MH = H’M’ (ΔMHH′=ΔH′M′M)
Lời giải
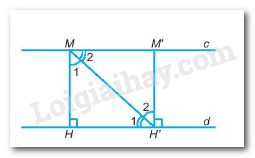
Lấy M, M’ thuộc c (M khác M’), kẻ MH, M’H’ vuông góc với d.
⇒MH∥M′H′
Xét ΔMHH′ và ΔH′M′Mcó:
MH’: chung
^M1=^H′2(soletrong)^M2=^H′1(soletrong)⇒ΔMHH′=ΔH′M′M(g−c−g)⇒MH=H′M′
Vậy khoảng cách từ mọi điểm thuộc c đến đường thẳng d bằng nhau và bằng khoảng cách từ mọi điểm thuộc đường thẳng d đến đường thẳng c.
Bài 9.6 trang 50 sách bài tập Toán 7: Cho 2 điểm phân biệt M, M’ ở cùng phía đối với đường thẳng d (M, M’ không thuộc d). Chứng minh rằng nếu M, M’ có cùng khoảng cách đến đường thẳng d thì MM’ song song với d.
Phương pháp giải
-Kẻ MH⊥d,M′H′⊥d
-Chứng minh: ΔMHH′=ΔH′M′M
Lời giải
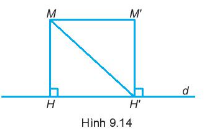
Kẻ MH⊥d,M′H′⊥d
⇒MH∥M′H′
Xét ΔMHH′ và ΔH′M′Mcó:
MH’:chung
MH = H’M’ (gt)
^HMH′=^M′H′M(soletrong)⇒ΔMHH′=ΔH′M′M(g−c−g)⇒^MH′H=^H′MM′(gtu)
Mà 2 góc ở vị trí so le trong nên MM′∥d (Dấu hiệu nhận biết 2 đường thẳng song song).
Cho góc xOy. Dùng thước hai lề dựng cặp đường thẳng song song gồm đường thẳng chứa tia Ox và đường thẳng x’ (sao cho x’ cắt Oy) rồi dùng thước hai lề đó, dựng cặp đường thẳng song song gồm đường thẳng chứa tia Oy và đường thẳng y’ (sao cho y’ cắt Ox).Hai đường thẳng x’ và y’ cắt nhau tại P. Chứng minh rằng tia OP là tia phân giác của góc xOy.
Phương pháp giải
-Áp dụng: Điểm nằm trong góc và cách đều 2 cạnh của góc thì nằm trên tia phân giác của góc đó.
-Vẽ hình như hình bên và chứng minh khoảng cách từ P đến Ox, Oy là bằng nhau.
Lời giải
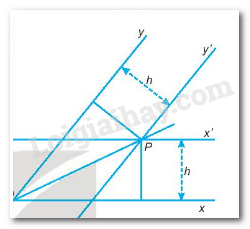
Ta có:
P thuộc x’,x cách x’ khoảng bằng h
⇒P cách x khoảng cách h (chứng minh bài 9.5)
P thuộc y’, y cách y’ khoảng bằng h
⇒ P cách y khoảng bằng h
⇒ P cách đều 2 đường thẳng 0x, Oy
Mà P nằm trong góc xOy (cách dựng)
⇒ P nằm trên tia phân giác của góc xOy.
Phương pháp giải
- Kẻ BI⊥AC;CK⊥AB
- Chứng minh: ΔBCK=ΔCBI(cạnh huyền – góc nhọn)
Lời giải
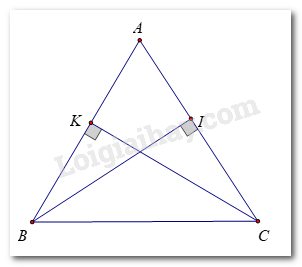
Kẻ BI⊥AC;CK⊥AB
Xét ΔBCKvà ΔCBIcó:
BC: cạnh chung
^BKC=^CIB=900
ˆB=ˆC(2 góc ở đáy BC của tam giác cân ABC)
⇒ΔBCK=ΔCBI(cạnh huyền – góc nhọn)
⇒CK=BI(cạnh tương ứng)
Vậy khoảng cách từ B đến đường thẳng AC bằng khoảng cách từ C đến đường thẳng AB.
Bài 9.9 trang 50 sách bài tập Toán 7: Cho tam giác ABC cân tại A và một điểm M tuỳ ý thuộc đoạn thẳng BC. Chứng minh rằng tổng khoảng cách từ điểm M đến đường thẳng AB, AC là một số không đổi
Phương pháp giải
- Xét khi M trùng B, C và khi M khác B, C
- Kẻ MP⊥AC;MQ⊥AB
-Chứng minh: ΔRBM cân tại R
-Chứng minh: MP + MQ = BS + SI = BI = CK.
Lời giải
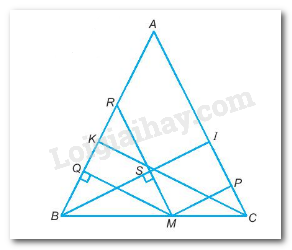
TH1:Khi M trùng với B hay C thì tổng khoảng cách đó là BI hoặc CK
Theo bài 9.8: BI = CK
TH2: Khi M khác B, khác C
Kẻ MP⊥AC;MQ⊥AB
⇒Tổng khoảng cách đang xét: MQ + MP
Qua M kẻ MR//AC; MR cắt BI tại S.
⇒ˆC=^RMB (2 góc đồng vị)
Mà ˆC=ˆB
⇒ˆB=^RMB
⇒ΔRBM cân tại R
MQ là khoảng cách từ M đến RB, BS là khoảng cách từ B đến RM
Theo bài 9.8: MQ = BS
Ta có: MR // AC, MP và SI có độ dài là khoảng cách giữa hai đường thẳng đó nên MP = SI
Suy ra: MP + MQ = BS + SI = BI = CK.
Xem thêm các bài giải SBT Toán lớp 7 Kết nối với tri thức hay, chi tiết khác:
Bài 31: Quan hệ giữa góc và cạnh đối diện trong một tam giác
Bài 33: Quan hệ giữa ba cạnh của tam giác
Bài 34: Sự đồng quy của ba đường trung tuyến, ba đường phân giác trong một tam
Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.