Với Giải SBT Toán 7 Bài 9.21 trang 58 Tập 2 trong Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác Sách bài tập Toán lớp 7 Tập 2 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 7.
Gọi H là trực tâm của tam giác nhọn ABC. Khi AH = BC, hãy chứng minh
Bài 9.21 trang 58 sách bài tập Toán 7: Gọi H là trực tâm của tam giác nhọn ABC. Khi AH = BC, hãy chứng minh .
Phương pháp giải
-Kẻ đường cao BJ của tam giác ABC.
-Chứng minh:
-Chứng minh tam giác ABJ vuông cân tại J.
Lời giải
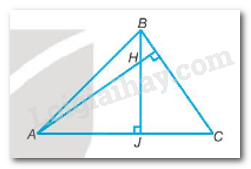
Gọi BJ là đường cao xuất phát từ B của tam giác ABC
Xét và có:
(cạnh tương ứng)
Mà tam giác JAB vuông tại J nên JAB là tam giác vuông cân.
Vậy
Xem thêm lời giải sách bài tập Toán 7 lớp 7 Kết nối tri thức với cuộc sống hay, chi tiết khác:
Xem thêm các bài giải SBT Toán lớp 7 Kết nối với tri thức hay, chi tiết khác:
Bài 34: Sự đồng quy của ba đường trung tuyến, ba đường phân giác trong một tam
Bài 36: Hình hộp chữ nhật và hình lập phương
Bài 37: Hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.