Toptailieu biên soạn và giới thiệu giải sách bài tập Toán 7 Bài 3 (Cánh diều): Hai đường thẳng song song hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm các bài tập từ đó nâng cao kiến thức và biết cách vận dụng phương pháp giải vào các bài tập trong SBT Toán 7 Bài 3.
Nội dung bài viết
Sách bài tập Toán 7 Bài 3 (Cánh diều): Hai đường thẳng song song
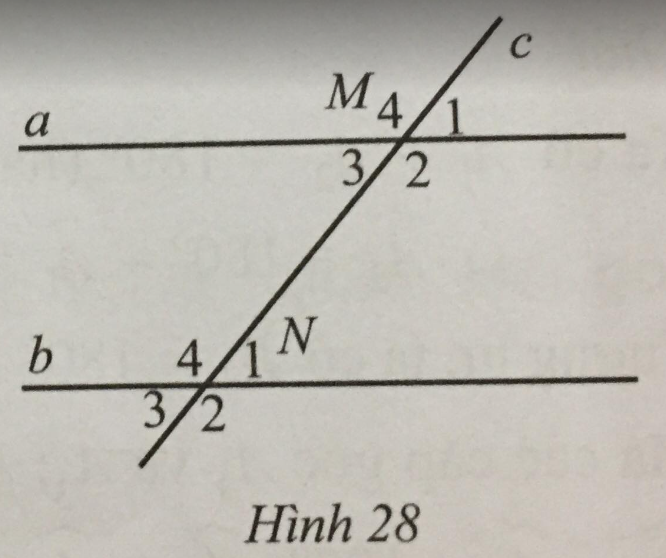
Bài 16 trang 110 sách bài tập Toán 7: Quan sát Hình 28, biết a // b, ^M3=50∘ˆM3=50∘.
a) Nêu những cặp góc so le trong, những cặp góc đồng vị.
b) Tìm số đo mỗi góc còn lại của đỉnh M và N.
Lời giải:
a) Những cặp góc so le trong là ^M1 và ^N3, ^M2 và ^N4, ^M3 và ^N1, ^M4 và ^N2.
Những cặp góc đồng vị là ^M1 và ^N1, ^M2 và ^N2, ^M3 và ^N3, ^M4 và ^N4.
b) Ta có: Hai góc so le trong thì bằng nhau, hai góc đồng vị thì bằng nhau nên ^M3=^N1=^M1=^N3=50∘.
Mà M1 và M4 là hai góc kề bù nhau nên ^M1=^M4=180∘⇒^M4=180∘−^M1=180∘−50∘=130∘.
Suy ra M4=N2=M2=N4=130∘.
Lời giải:
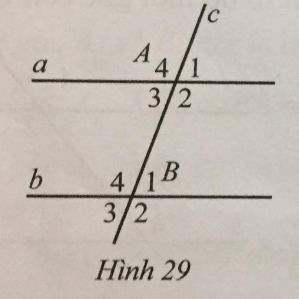
Ta có 3^A1=2^A2 hay ^A2=32^A1 và ^A1+^A2=180∘ (hai góc kề bù) nên
^A1+32^A1=52^A1=180∘→^A1=72∘⇒^A2=32.72∘=108∘
Mà a // b nên ^A3=^B1=^A1=^B3=72∘ , ^A4=^B2=^A2=^B4=108∘ (các góc so le trong và đồng vị).
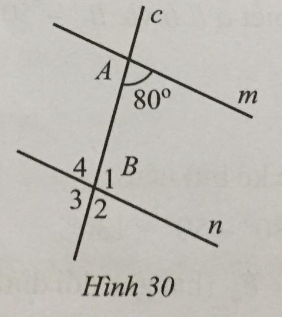
Bài 18 trang 110 sách bài tập Toán 7: Tìm số đo mỗi góc B1,B2,B3,B4 trong Hình 30, biết m //n.
Lời giải chi tiết
Ta có: m // n nên ^B4=^B2=80∘ (hai góc so le trong và đồng vị với góc bằng 80°)
Mà ^B1+^B4=180∘ (hai góc kề bù) nên ^B1=^B3=180∘−80∘=100∘.
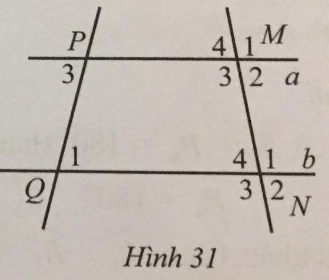
Lời giải:
Ta có: ^P3=^Q1. Mà 2 góc này ở vị trí so le trong nên nên a // b (Dấu hiệu nhận biết 2 đường thẳng song song)
Ta có: ^M3+^M4=180∘ (hai góc kề bù) nên ^M4=180∘−^M3=180∘−100∘=80∘.
Suy ra: ^M3=^N1=^M1=^N3=100∘, ^M4=^N2=^M2=^N4=80∘.
Bài 20 trang 110 sách bài tập Toán 7: Tìm số đo x, y trong Hình 32.
Lời giải:
a) Do ^aAc=^bDc và chúng ở vị trí đồng vị nên aa’ // bb’ (Dấu hiệu nhận biết 2 đường thẳng song song)
Suy ra x=^bCd′=45∘ (hai góc so le ngoài).
b) Ta có: ^qNm′+^m′Nq′=180∘ (hai góc kề bù) nên ^qNm′=180∘−^m′Nq′=180∘−50∘=130∘.
Suy ra ^qNm′=^qQn′=130∘. Mà 2 góc này ở vị trí đồng vị nên mm’ // nn’ (Dấu hiệu nhận biết 2 đường thẳng song song)
Vậy y=^pPn′=75∘ (hai góc so le ngoài).
Bài 21 trang 111 sách bài tập Toán 7: Tìm số đo góc BCD trong Hình 33.
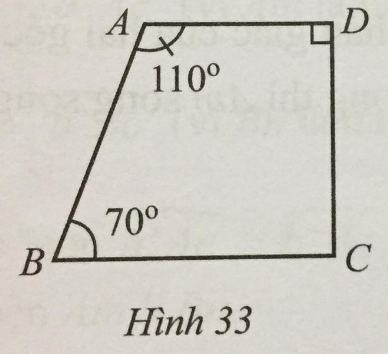
Lời giải:
Ta có: ˆA+ˆB=110∘+70∘=180∘ nên hai góc này bù nhau mà chúng ở vị trí trong cùng phía nên AD // BC.
Suy ra ˆD+ˆC=180∘ (hai góc trong cùng phía) nên ^BCD=180∘−ˆD=180∘−90∘=90∘.
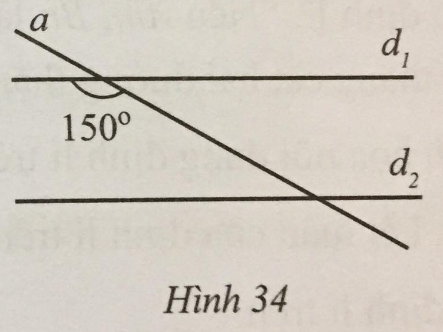
Lời giải:
Ta có d1 // d2 nên góc tạo bởi đường thẳng a và đường thẳng d1 với góc nhọn tạo bởi đường thẳng a và đường thẳng d2 bù nhau.
Suy ra góc nhọn tạo bởi đường thẳng a và đường thẳng d2 bằng 180∘−150∘=30∘.

Lời giải:
Do xx’ // zz’ nên ^ACz=^CAz′ (hai góc so le trong)
Do yy’ // zz’ nên ^BCz=^CBy′ (hai góc so le trong)
Vậy ^ACB=^ACz+^BCz=^CAx′+^CBy′.
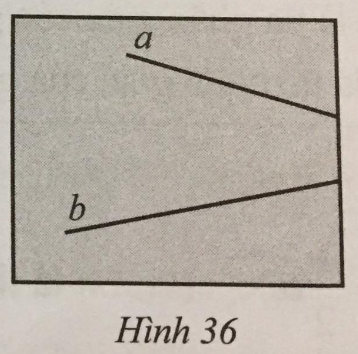
Lời giải:
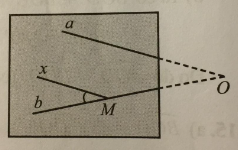
Lấy M∈b. Kẻ Mx // a với ^bMx<90∘. Khi đó góc nhọn tạo bởi hai đường thẳng a và b đã vẽ chính là góc bMx vì chúng nằm ở vị trí đồng vị. Vậy ta chỉ cần đo góc bMx sẽ ra được góc nhọn tạo bởi hai đường thẳng a và b đã vẽ.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.