Toptailieu biên soạn và giới thiệu giải sách bài tập Toán 7 Bài 1 (Cánh diều): Góc ở vị trí đặc biệt hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm các bài tập từ đó nâng cao kiến thức và biết cách vận dụng phương pháp giải vào các bài tập trong SBT Toán 7 Bài 1.
Nội dung bài viết
Sách bài tập Toán 7 Bài 1 (Cánh diều): Góc ở vị trí đặc biệt
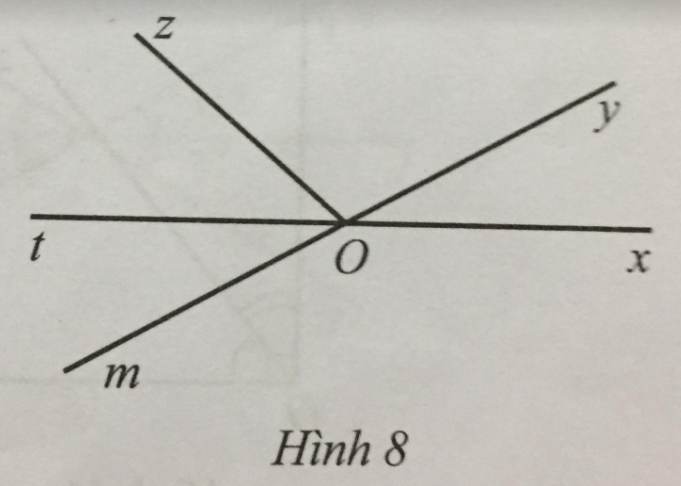
Bài 1 trang 103 sách bài tập Toán 7: Quan sát Hình 8 và chỉ ra:
a) Bốn cặp góc kề nhau;
b) Ba cặp góc kề bù (khác góc bẹt);
c) Hai cặp góc đối đỉnh (khác góc bẹt và góc không).
Lời giải:
a) Bốn cặp góc kề nhau là xOy và yOz, xOy và yOt, yOz và zOt, yOz và zOm;
b) Ba cặp góc kề bù (khác góc bẹt) là xOy và yOt, yOz và zOm, tOm và mOx;
c) Hai cặp góc đối đỉnh (khác góc bẹt và góc vuông) là xOy và tOm, yOt và mOx.
a) ^aOc=75∘; b) ^aOc+^bOd=140∘;
c) ^aOc+^bOd=^bOc+^aOd; d) ^bOc−^aOc=10∘;
e) ^bOc=2^aOc.
Lời giải:
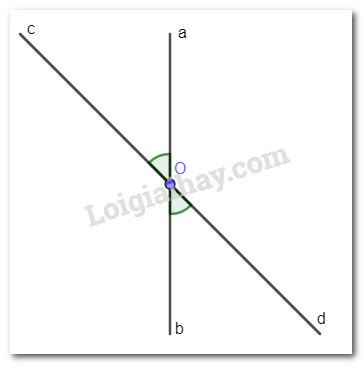
a) ^aOc=^bOd=75∘ (đối đỉnh); ^bOc=^aOd=180∘−75∘=105∘ (hai góc aOc và bOd bù nhau).
b) ^aOc+^bOd=140∘→^aOc=^bOd=140∘:2=70∘; ^bOc=^aOd=180∘−70∘=110∘.
c)
^aOc+^bOd=^bOc+^aOd→2^aOc=2^bOc→^aOc=^bOd=180∘:2∘=90∘→^aOc=^bOd=^bOc=^aOd=90;
d)
{^bOc+^aOc=180∘^bOc−^aOc=10∘→{^bOc=^aOd=95∘^aOc=^bOd=85∘;
e)
{^bOc+^aOc=180∘^bOc=2^aOc→3^aOc=180∘→^aOc=^bOd=60∘→^bOc=^aOd=120∘
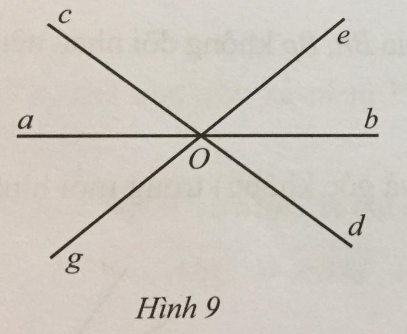
Bài 3 trang 104 sách bài tập Toán 7: Quan sát Hình 9.
a) Hai góc aOg và cOe có phải là hai góc đối đỉnh hay không? Vì sao?
b) Tìm các cặp đối đỉnh (khác góc bẹt và góc không) ở Hình 9.
c) Chứng tỏ rằng ^aOg+^cOe+^bOd=180∘.
Lời giải:
a) Hai góc aOg và cOe không phải là hai góc đối đỉnh. Vì Og và Oe là hai tia đối nhưng Oa và Oc không là hai tia đối.
b) Các cặp góc đối đỉnh là aOc và bOd, cOe và dOg, bOe và aOg, aOe và bOg, bOc và aOd, cOg và dOe.
c) Ta có: ^aOc=^bOd (đối đỉnh)
nên: ^aOg+^cOe+^bOd=^aOg+^cOe+^aOc=^gOe=180∘.
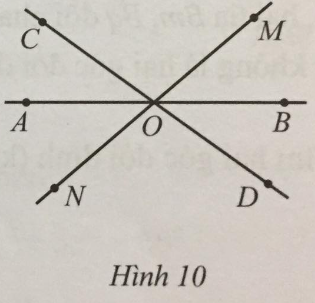
Bài 4 trang 104 sách bài tập Toán 7: Quan sát Hình 10 và chỉ ra:
a) Bốn góc kề với góc AOC (không kể góc bẹt);
b) Hai góc kề bù với góc AOC.
Lời giải:
a) Bốn góc kề với góc AOC (không kể góc bẹt) là COM, COB, AON, AOD;
b) Hai góc kề bù với góc AOC là COB, AOD.
Bài 5 trang 104 sách bài tập Toán 7: Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?
a) Hai góc đối đỉnh thì bằng nhau.
b) Hai góc bằng nhau thì đối đỉnh.
c) Hai góc không đối đỉnh thì không bằng nhau.
Lời giải:
Phát biểu a) đúng.
Phát biểu b) sai.
Phát biểu c) sai.
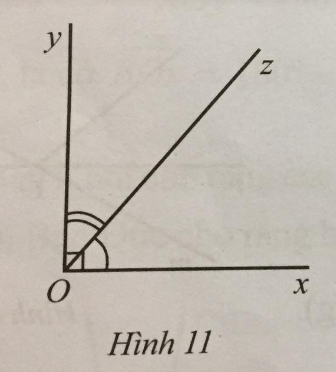
Lời giải:
Ta có: 15^xOz=14^yOz→^xOz=54^yOz.
Do hai góc xOz và yOz là hai góc kề nhau nên ^xOz+^yOz=^xOy=90∘.
Do đó: 54^yOz+^yOz=90∘→94^yOz=90∘→^yOz=90∘:94=40∘.
Suy ra: ^xOz=90∘−^yOz=90∘−40∘=50∘.
a) Tính số đo mỗi góc xOy, yOz.
b) Vẽ các tia Ox’ và Oy’ lần lượt là tia đối của các tia Ox, Oy. Tính số đo mỗi góc x’Oy’, y’Oz, xOy’.

Lời giải:
a) Do hai góc xOy, yOz là hai góc kề nhau, ^xOz=150∘ nên ^xOy+^yOz=150∘.
Ta có:
{^xOy−^yOz=90∘^xOy+^yOz=150∘→{^xOy=120∘^yOz=30∘
Vậy {^xOy=120∘^yOz=30∘.
b)
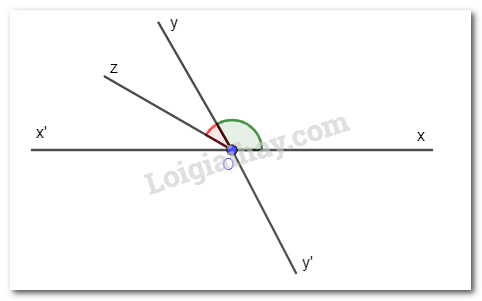
Ta có: ^x′Oy′=^xOy=120∘ (đối đỉnh).
Ta có: ^y′Oz+^yOz=180∘ (hai góc kề bù). Suy ra: ^y′Oz=180∘−^yOz=180∘−30∘=150∘.
Tương tự, ta có: ^xOy′=180∘−^xOy=180∘−120∘=60∘.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.