Toptailieu biên soạn và giới thiệu giải sách bài tập Toán 7 (Cánh diều) Bài tập cuối chương 4 hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm các bài tập từ đó nâng cao kiến thức và biết cách vận dụng phương pháp giải vào các bài tập trong SBT Toán 7 Bài 1 .
Nội dung bài viết
Sách bài tập Toán 7 (Cánh diều) Bài tập cuối chương 4
Bài 29 trang 114 sách bài tập Toán 7: Số đo của góc xOt trong Hình 39 là:
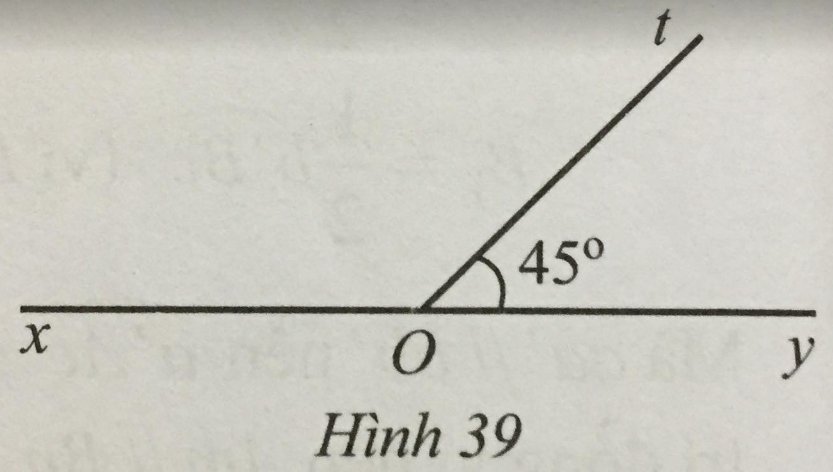
A. 45°. B. 135°.
C. 55°. D. 90°.
Lời giải:
Ta có: Góc xOt và yOt là hai góc kề nhau nên
^xOt+^yOt=^xOy→^xOt+45∘=180∘⇒^xOt=180∘−45∘=135∘
Đáp án: B. 135°
A. 56°. B. 62°. C. 28°. D. 23°.
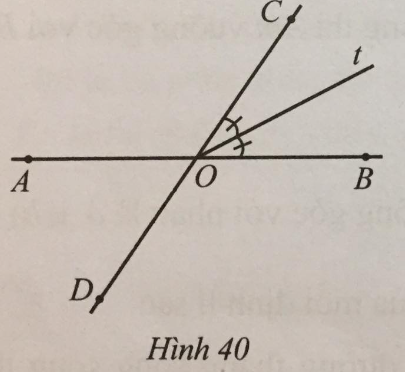
Lời giải:
Ta có: ^BOC=^AOD (đối đỉnh).
Suy ra: ^AOC−^BOC=^AOC−^AOD=68∘ mà ^AOC+^AOD=180∘.
Suy ra: {^AOC=124∘^AOD=^BOC=56∘.
Mà Ot là tia phân giác của góc BOC nên ^BOt=12^BOC=56∘2=28∘.
Đáp án: C. 28°.
Bài 31 trang 14 sách bài tập Toán 7: Cho Hình 41 có ^A1=^B3=60∘. Kết luận nào sau đây là sai?
A. ^A3=60∘. B. ^B1=60∘.
C. ^A4=120∘. D. ^B2=60∘.
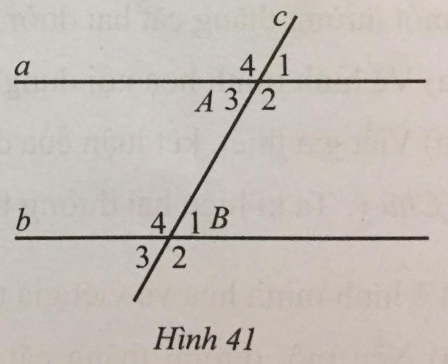
Lời giải:
Ta có: ^A1=^A3=^B3=^B1=60∘ (các góc này đối đỉnh với nhau).
Mà góc A3,A4 là hai góc bề bù nhau nên A4 = 180° - 60° = 120° = B2 (hai góc so le ngoài).
Đáp án: D. ^B2=60∘.
Bài 32 trang 114 sách bài tập Toán 7: Quan sát Hình 42. Tổng số đo hai góc A1 và B1 là:
A. 110°. B. 240°
C. 180°. D. 220°.
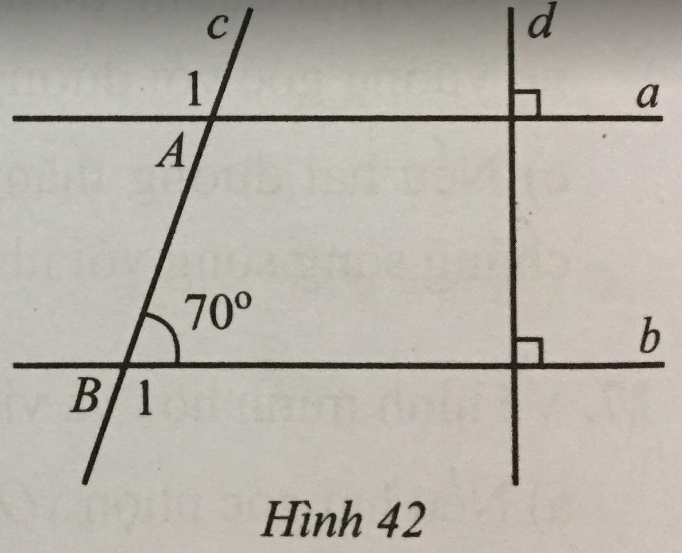
Lời giải:
Ta có a // b nên ^A1=^B1 (hai góc so le ngoài).
Vậy ^A1+^B1=2.(180∘−70∘)=2.110∘=220∘.
Đáp án: D. 220°.
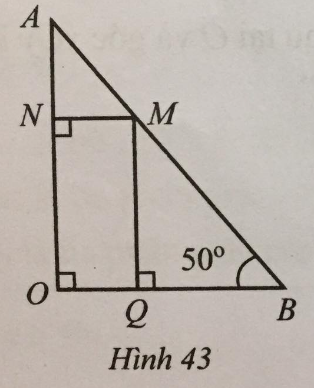
Lời giải:
Vì MN⊥OA;OB⊥OA⇒MN//OB (cùng vuông góc với OA)
⇒^NMQ=^MQB (2 góc so le trong); ^NMA=^OBA (2 góc đồng vị)
Mà ^MQB=90∘;^OBA=500 nên ^NMQ=900;^NMA=500;
Vì ^BMQ+^QMN+^NMA=1800 nên ^BMQ=1800−900−500=40∘.
Ta có: NO⊥OB;MQ⊥OB⇒NO//MQ (cùng vuông góc với OB) nên ^MAN=^BMQ=40∘ (hai góc đồng vị).
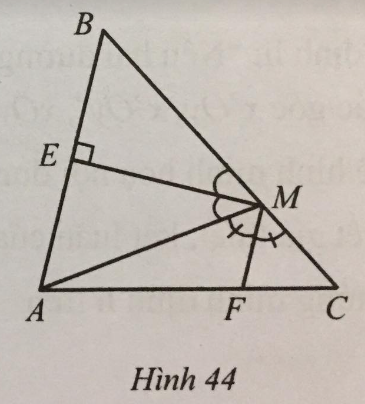
Lời giải:
Do hai góc AME và AMF là hai góc kề nhau nên ^EMF=^AME+^AMF.
Ta có ME, MF lần lượt là tia phân giác của góc AMB và AMC nên
^AME=12^AMB;^AMF=12^AMC.
Mà ^AMB+^AMC=180∘ (hai góc kề bù) nên
^EMF=^AME+^AMF=12(^AMB+^AMC)=12.180∘=90∘.
Suy ra: ^EMF=^MEB mà hai góc này ở vị trí so le trong nên MF // AB (Dấu hiệu nhận biết 2 đường thẳng song song)
a) Tính số đo mỗi góc AOB, BOC.
b) Tia OD có là tia phân giác của góc AOB hay không?
c) So sánh hai góc AOC và BOC’.
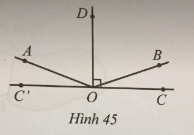
Lời giải:
a) Do hai góc AOC và BOC là hai góc kề nhau nên ^AOB+^BOC=^AOC=160∘.
Mà ^AOB−^BOC=120∘ nên {^AOB=140∘^BOC=20∘
b) Ta có OD⊥CC′→^COD=90∘.
Do đó góc AOD và COD là hai góc kề nhau nên ^AOD+^COD=^AOC.
Suy ra: ^AOD=^AOC−^COD=160∘−90∘=70∘.
Tương tự, ta có: ^BOD=^COD−^BOC=90∘−20∘=70∘.
Do đó: ^AOD=^BOD. Mà OD nằm giữa hai tia OA và OB nên OD là tia phân giác của góc AOB.
c) Ta có ^BOC′+^BOC=180∘ (hai góc kề bù) nên ^BOC′=180∘−^BOC=180∘−20∘=160∘.
Vậy ^AOC=^BOC′.
a) Hai góc xOt và yOz có bằng nhau hay không?
b) Chứng tỏ ^xOy+^zOt=180∘.
c) Vẽ tia Ou là tia phân giác của góc tOz. Tia Ou có phải là tia phân giác của góc xOy hay không?
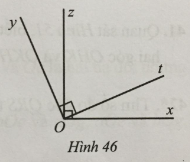
Lời giải chi tiết
a) Ta có: các cặp góc xOt và zOt, yOt và zOt là các cặp góc kề nahu nên
^xOt+^zOt=^xOz=90∘,^yOz+^zOt=^yOt=90∘.
Do đó: ^xOt=^yOz.
b) Ta có hai góc yOz và xOz là hai góc kề nhau nên ^yOz+^xOz=^xOy.
Suy ra: ^xOy+^zOt=^yOz+^xOz+^zOt=^xOz+(^yOz+^zOt)=^yOz+^zOt=90∘+90∘=180∘
c)
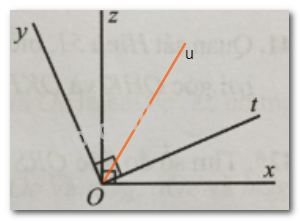
Do Ou là tia phân giác của góc tOz nên ^tOu=^zOu.
Ta có: các cặp góc tOu và xOt, zOu và yOz là các cặp góc kề nhau nên ^tOu+^xOt=^xOu,^zOu+^yOz=^yOu.
Mà ^tOu=^zOu,^xOt=^yOz⇒^xOu=^yOu.
Mà Ou nằm giữa hai tia Ox và Oy nên Ou là tia phân giác của góc xOy.
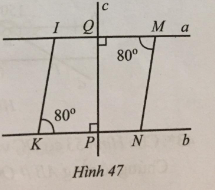
Bài 37 trang 115 sách bài tập Toán 7: Quan sát Hình 47.
a) Vì sao hai đường thẳng a và b song song với nhau?
b) Tìm số đo góc MIK.
c) Vì sao hai đường thẳng MN và IK song song với nhau?
Lời giải:
a) Ta có: ^aQP=^KPc=90∘ mà hai góc này ở vị trí so le trong nên a // b (Dấu hiệu nhận biết 2 đường thẳng song song)
b) Vì a//b nên ^MIK+^IKN=1800 (2 góc trong cùng phía)
⇒^MIK+800=1800
⇒^MIK=1800−800=1000
c) Ta có ^MNb=180∘−^MNP=180∘−100∘=80∘.
Suy ra: ^MNb=^bKI mà hai góc này ở vị trí đồng vị nên MN // IK.
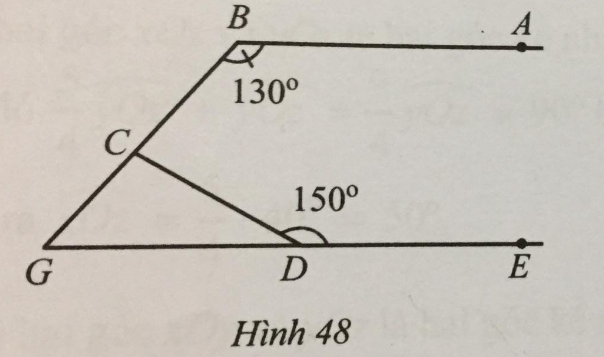
Bài 38 trang 115 sách bài tập Toán 7: Tìm số đo góc BCD trong Hình 48, biết AB // DE.
Lời giải:
Ta có AB // DE nên hai góc ABG và EGB là hai góc trong bù nhau.
Suy ra: ^EGB=180∘−^ABG=180∘−130∘=50∘.
Mặt khác hai góc CDG và CDE kề bù nhau nên ^CDG=180∘−^CDE=180∘−150∘=30∘.
Xét tam giác CGD có tổng ba góc trong một tam giác bằng 180° nên ^DCG=180∘−50∘−30∘=100∘.
Mà hai góc DCG và BCD kề bù nhau nên BCD=180∘−100∘=80∘.
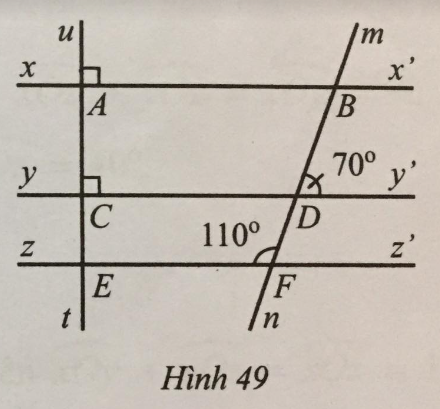
Bài 39 trang 115 sách bài tập Toán 7: Quan sát Hình 49. Chứng tỏ:
a) yy’ // zz’; b) ut⊥zz′; c) xx’ // zz’.
Lời giải:
a) Ta có ^DFE+^DFz′=180∘ (hai góc kề bù) nên ^DFz′=180∘−^DFE=180∘−110∘=70∘.
Do đó ^DFz′=^BDy′ mà hai góc này ở vị trí đồng vị nên yy’ // zz’.
b) Do yy’ // zz’ nên ^uEz′=^uCy′=90∘⇒ut⊥zz′.
c) Ta có ^uAx′=^uEz′=90∘ và chúng ở vị trí đồng vị nên xx’ // zz’ (Dấu hiệu nhận biết 2 đường thẳng song song)
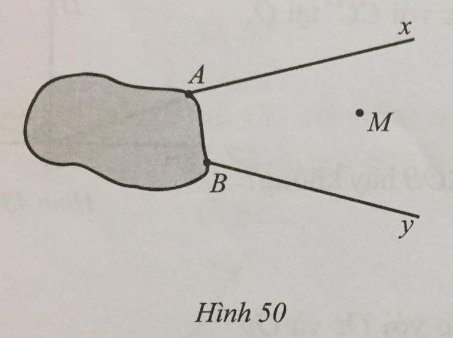
Lời giải:
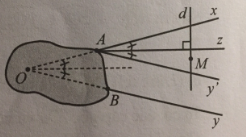
Kẻ Ay’ // By, khi đó ta có ^xAy′=^xOy (hai góc đồng vị). Vẽ tia Az là tia phân giác của góc xAy’, suy ra:
^xAz=12^xAy′=12^xOy.
Suy ra góc xAz bằng góc phân giác của góc xOy mà chúng ở vị trí đồng vị nên Az song song với tia phân giác của góc xOy. Như vậy, qua điểm M kẻ đường thẳng d vuông góc với Az thì đường thẳng d là đường thẳng đi qua M và vuông góc với tia phân giác của góc xOy.
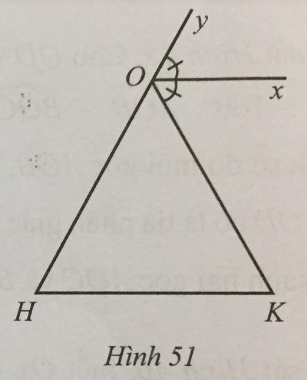
Lời giải:
Ta có: Ox // HK nên ^yOx=^OHK (hai góc đồng vị) và ^xOK=^OKH (hai góc so le trong).
Mà Ox là tia phân giác của góc yOK nên hai góc yOx và xOK bằng nhau.
Vậy hai góc OHK và OKH bằng nhau.
Bài 42 trang 116 sách bài tập Toán 7: Tìm số đo góc QRS trong Hình 52, biết aa’ // cc’.
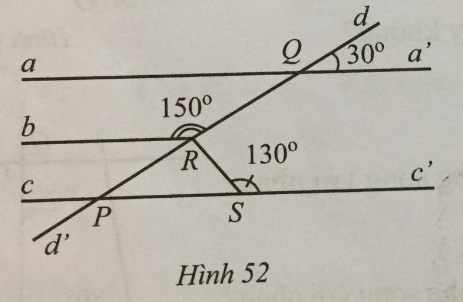
Lời giải:
Ta có aa’ // cc’ nên ^dQa′=^aQd′=30∘ (đối đỉnh).
Mà tổng của hai góc trong aQR và bRQ bằng 180°. Suy ra aa’ // bb’ // cc’.
Ta có aa’ // cc’ nên ^dQa′=^dPc′=30∘ (hai góc đồng vị).
Mặt khác: hai góc RSc’ và RSP (RSc’) kề bù nhau nên .
Xét tam giác RPS có tổng ba góc trong một tam giác bằng 180° nên .
Mà hai góc PRS và QRS kề bù nhau nên .
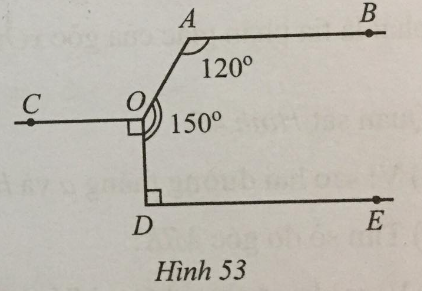
Lời giải:
Ta có: OC và DE cùng vuông góc với OD nên OC // DE.
Ta có: .
Suy ra: mà hai góc này ở vị trí so le trong nên OC // AB.
Vậy AB // OC // DE.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.