Toán 7 Kết nối tri thức: Bài tập cuối chương IV

thuyen nguyen Ngày: 01-02-2023 Lớp 7

1 K

Toptailieu.vn giới thiệu Giải bài tập Toán lớp 7 trang 87 Bài tập cuối chương IV sách Kết nối tri thức giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 7 Tập 1. Mời các bạn đón xem:

Giải SGK Toán 7 (Kết nối tri thức): Bài tập cuối chương IV

Bài tập

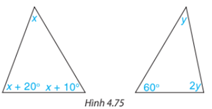
Bài 4.33 trang 87 SGK Toán 7 tập 1: Tính các số đo x, y trong tam giác dưới đây (H.4.75)

Phương pháp giải

Áp dụng tổng 3 góc của 1 tam giác bằng 180 độ.

Lời giải

Áp dụng định lí tổng ba góc trong tam giác,

+) Ta có:

$\begin{array}{l} x + x + 20^{o} + x + 10^{o} = 180^{o} \\ \Rightarrow 3 x = 150^{o} \\ \Rightarrow x = 50^{o} \end{array}$

+) Ta có:

$\begin{array}{l} y + 60^{o} + 2 y = 180^{o} \\ \Rightarrow 3 y = 120^{o} \\ \Rightarrow y = 40^{o} \end{array}$

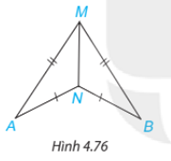
Bài 4.34 trang 87 SGK Toán 7 tập 1: Trong Hình 4.76, có AM = BM, AN = BN. Chứng minh rằng $\hat{M A N} = \hat{M B N}$ .

Phương pháp giải

Chứng minh 2 tam giác MNA và MNB bằng nhau từ đó suy ra 2 góc tương ứng bằng nhau.

Lời giải

Xét 2 tam giác MNA và MNB có:

AM=BM

AN=BN

MN chung

=> $Δ M N A = Δ M N B$ (c.c.c)

=> $\hat{M A N} = \hat{M B N}$ (2 góc tương ứng)

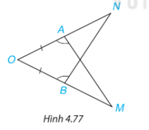
Bài 4.35 trang 87 SGK Toán 7 Tập 1: Trong Hình 4.77, có AO = BO, $\hat{O A M} = \hat{O B N}$ . Chứng minh rằng AM = BN.

Phương pháp giải

Chứng minh 2 tam giác OAM và OBN bằng nhau từ đó suy ra AM=BN.

Lời giải

Xét 2 tam giác OAM và OBN có:

$\hat{O A M} = \hat{O B N}$

AO=BO

Góc O chung

=> $Δ O A M = Δ O B N$ (g.c.g)

=>AM=BN (2 cạnh tương ứng)

Bài 4.36 trang 87 SGK Toán 7 Tập 1: Trong Hình 4.78, ta có AN = BM, $\hat{B A N} = \hat{A B M}$ . Chứng minh rằng $\hat{B A M} = \hat{A B N}$ .

Phương pháp giải

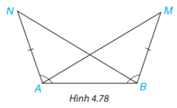
Chứng minh 2 tam giác ANB và BMA bằng nhau từ đó suy ra $\hat{B A M} = \hat{A B N}$ .

Lời giải

Xét 2 tam giác ANB và BMA có:

AN=BM

$\hat{B A N} = \hat{A B M}$

AB chung

=> $Δ A N B = Δ B M A$ (c.g.c)

Bài 4.37 trang 87 SGK Toán 7 Tập 1: Cho M, N là hai điểm phân biệt nằm trên đường trung trực của đoạn thẳng AB sao cho AM = AN. Theo em, tứ giác AMBN là hình gì?

Phương pháp giải

Chứng minh 4 cạnh của tứ giác bằng nhau.

Lời giải

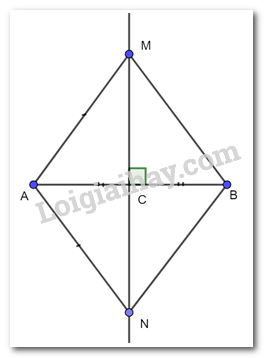
Vì M, N nằm trên đường trung trực của AB nên MA = MB ; NA = NB ( tính chất)

Mà MA = NA (gt)

Vậy MA = NA = MB = NB nên tứ giác AMBN là hình thoi

Bài 4.38 trang 87 SGK Toán 7 Tập 1: Cho tam giác ABC cân tại A có $\hat{A} = 120^{\circ}$ . Trên cạnh BC lấy hai điểm M, N sao cho MA, NA lần lượt vuông góc với AB, AC. Chứng minh rằng:

a) $Δ$ BAM = $Δ$ CAN;

b) Các tam giác ANB, AMC lần lượt cân tại N, M.

Phương pháp giải

a) Chứng minh 2 tam giác bằng nhau theo trường hợp g-c-g

b) Chứng minh tam giác có 2 cạnh bằng nhau hoặc 2 góc bằng nhau

Lời giải

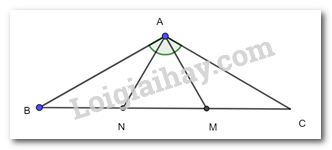
a) Xét 2 tam giác vuông BAM và CAN có:

AB=AC(Do tam giác ABC cân tại A)

$\hat{B} = \hat{C}$ (Do tam giác ABC cân tại A)

=> $Δ B A M = Δ C A N$ (g.c.g)

Xét tam giác ABC cân tại A, có $\hat{A} = 120^{\circ}$ có:

$\hat{B} = \hat{C} = \frac{180^{o} - 120^{o}}{2} = 30^{o}$ .

Xét tam giác ABM vuông tại A có:

$\begin{array}{l} \hat{B} + \hat{B A M} + \hat{A M B} = 180^{o} \\ \Rightarrow 30^{o} + 90^{o} + \hat{A M B} = 180^{o} \\ \Rightarrow \hat{A M B} = 60^{o} \\ \Rightarrow \hat{A M C} = 180^{o} - \hat{A M B} = 180^{o} - 60^{o} = 120^{o} \end{array}$

Xét tam giác MAC có:

$\begin{array}{l} \hat{A M C} + \hat{M A C} + \hat{C} = 180^{o} \\ \Rightarrow 120^{o} + \hat{M A C} + 30^{o} = 180^{o} \\ \Rightarrow \hat{M A C} = 30^{o} = \hat{C} \end{array}$

$\Rightarrow$ Tam giác AMC cân tại M.

Vì $Δ B A M = Δ C A N$ =>BM=CN => BN=MC

Xét 2 tam giác ANB và AMC có:

AB=AC

$A N = A M$ (do $Δ B A M = Δ C A N$ )

BN=MC

=> $Δ A N B = Δ A M C$ (c.c.c)

Mà tam giác AMC cân tại M.

=> Tam giác ANB cân tại N.

Bài 4.39 trang 87 SGK Toán 7 Tập 1: Cho tam giác ABC vuông tại A có B = 60°. Trên cạnh BC lấy điểm M sao cho $\hat{C A M} = 30^{o}$ . Chứng minh rằng:

a) Tam giác CAM cân tại M;

b) Tam giác BAM là tam giác đều;

c) M là trung điểm của đoạn thẳng BC.

Phương pháp giải

a) Dùng tính chất tổng 3 góc trong 1 tam giác bằng 180 độ suy ra góc A bằng góc C.

b) Chứng minh tam giác ABM cân có 1 góc bằng 60 độ

c) Dùng tính chất tổng 3 góc trong 1 tam giác bằng 180 độ để tính số đo 3 góc từ đó suy ra tam giác đều

Lời giải

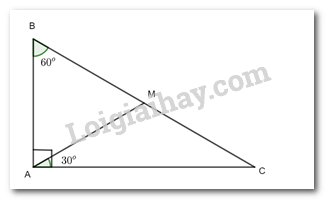
a) Xét tam giác ABC có:

$\begin{array}{l} \hat{A} + \hat{B} + \hat{C} = 180^{o} \\ => 90^{o} + 60^{o} + \hat{C} = 180^{o} \\ => \hat{C} = 30^{o} \end{array}$

Xét tam giác CAM có $\hat{A} = \hat{C} = 30^{o}$

=>Tam giác CAM cân tại M.

b) Xét tam giác ABM có:

$\begin{array}{l} \hat{C} + \hat{C M A} + \hat{C A M} = 180^{o} \\ => 30^{o} + \hat{C M A} + 30^{o} = 180^{o} \\ => \hat{C M A} = 120^{o} \\ => \hat{B M A} = 180^{o} - \hat{C M A} = 180^{o} - 120^{o} = 60^{o} \end{array}$