Toán 7 Kết nối tri thức: Luyện tập chung

thuyen nguyen Ngày: 01-02-2023 Lớp 7

820

Toptailieu.vn giới thiệu Giải bài tập Toán lớp 7 trang 86 Luyện tập chung sách Kết nối tri thức giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 7 Tập 1. Mời các bạn đón xem:

Giải SGK Toán 7 Kết nối tri thức: Luyện tập chung

Bài tập

Bài 4.29 trang 86 SGK Toán 7 Tập 1: Cho Hình 4.73. Hãy tính các độ dài a, b và số đo x, y của các góc trên hình vẽ.

Phương pháp giải

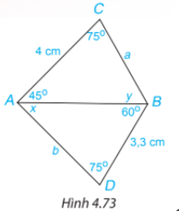
Áp dụng tổng ba góc trong một tam giác bằng 180 độ để tìm x,y.

Chứng minh 2 tam giác bằng nhau để tìm a,b.

Lời giải

Xét tam giác ABC có:

$\begin{array}{l} \hat{B A C} + \hat{A B C} + \hat{C} = 180^{o} \\ \Rightarrow 45^{o} + y + 75^{o} = 180^{o} \\ \Rightarrow y = 60^{o} \end{array}$

Xét tam giác ABD có:

$\begin{array}{l} \hat{D A B} + \hat{D B A} + \hat{D} = 180^{o} \\ \Rightarrow x + 60^{o} + 75^{o} = 180^{o} \\ \Rightarrow x = 45^{o} \end{array}$

Xét 2 tam giác ABC và ADB có:

$\hat{D A B} = \hat{C A B} = 45^{o}$

AB chung

$\hat{D} = \hat{C} = 75^{o}$

=> $Δ A B C = Δ A D B$ (g.c.g)

=>BC=BD ( 2 cạnh tương ứng), mà BD = 3,3 cm =>a= BC= 3,3cm

AC=AD ( 2 cạnh tương ứng), mà AC = 4 cm =>b = AD = 4cm

Bài 4.30 trang 86 SGK Toán 7 Tập 1: Cho góc xOy. Trên tia Ox lấy hai điểm A, M; trên tia Oy lấy hai điểm B, N sao cho OA = OB, OM =ON, OA > OM.

Chứng minh rằng:

a) $Δ$ OAN = $Δ$ OBM;

b) $Δ$ AMN = $Δ$ BNM.

Phương pháp giải

Chứng minh 2 tam giác bằng nhau theo trường hợp cạnh-góc-cạnh.

Lời giải

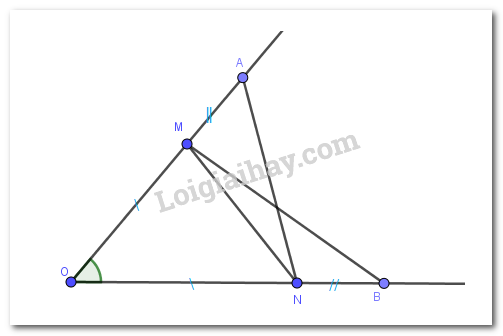
a) Xét tam giác OAN và OBM có:

OA=OB

$\hat{O}$ chung

OM=ON

=> $Δ O A N = Δ O B M$ (c.g.c)

b) Do $Δ O A N = Δ O B M$ nên AN=BM ( 2 cạnh tương ứng); $\hat{O A N} = \hat{O B M}$ ( 2 góc tương ứng) => $\hat{N A M} = \hat{M B N}$

Do OA + AM = OM; OB + BN = ON

Mà OA = OB, OM =ON

=> AM=BN

Xét hai tam giác AMN và BNM có:

AN=BM

$\hat{N A M} = \hat{M B N}$

AM=BN

=> $Δ A M N = Δ B N M$ (c.g.c)

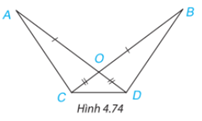
Bài 4.31 trang 86 SGK Toán 7 Tập 1: Cho Hình 4.74, biết OA = OB, OC = OD. Chứng minh rằng:

a) AC = BD;

b) $Δ$ ACD = $Δ$ BDC.

Phương pháp giải

a) Chứng minh 2 tam giác ACD và BDC bằng nhau.

b) Chỉ ra 3 cạnh của hai tam giác đó bằng nhau

Lời giải

Ta có: OA = OB, OC = OD nên AD=BC

Do OC=OD nên tam giác OCD cân => $\hat{O C D} = \hat{O D C}$

Xét 2 tam giác ACD và BDC có:

AD=BC

$\hat{O C D} = \hat{O D C}$

CD chung

=> $Δ A C D = Δ B C D$ (c.g.c)

=>AC=BD (hai cạnh tương ứng)

b)Xét hai tam giác ACD và BDC có:

AO=BO

CO=DO

AC=BD

=> $Δ A C D = Δ B D C$ (c.c.c)

Bài 4.32 trang 86 SGK Toán 7 Tập 1: Cho tam giác MBC vuông tại M có $\hat{B}$ = 60°. Gọi A là điểm nằm trên tia đối của tia MB sao cho MA = MB. Chứng minh rằng tam giác ABC là tam giác đều.

Phương pháp giải

Chứng minh tam giác ABC cân tại C và có 1 góc bằng 60 độ.

Lời giải

Xét 2 tam giác vuông CMB và CMA có:

MC chung

MB=MA

=> $Δ C M B = Δ C M A$ (c.g.c)

=>CA = CB (2 cạnh tương ứng).

=> Tam giác ABC cân tại C.

Mà góc B bằng 60^o

=>Tam giác ABC đều.

Từ khóa :

Giải bài tập Toán 7

Đánh giá

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Lớp 6

Toán 6 ( Kết nối tri thức): Luyện tập chung Mai Hương

295

Toán Lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

316

Toán Lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

344

Toán Lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

292