Toptailieu.vn giới thiệu Giải bài tập Toán lớp 7 Luyện tập chung trang 86 chi tiết sách Toán 7 Tập 1 Kết nối tri thức giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 7. Mời các bạn đón xem:
Nội dung bài viết
Giải bài tập Toán lớp 7 Luyện tập chung trang 86
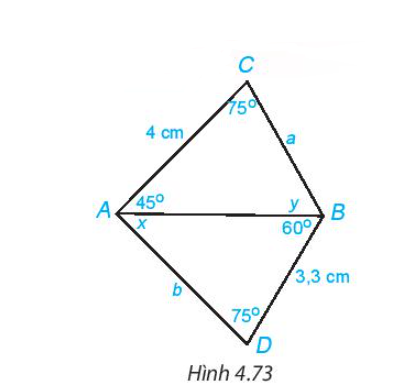
Lời giải:
Xét tam giác ABC có ^BAC+^ABC+^BCA=180°.
Do đó ^ABC=180°−^BAC−^BCA hay y=180°−45°−75°=60°.
Xét tam giác ABD có ^BAD+^ABD+^BDA=180°.
Do đó ^BAD=180°−^ABD−^BDA hay x=180°−60°−75°=45°.
Xét hai tam giác ABC và ABD có:
^CAB=^DAB (cùng bằng 45o).
AB chung.
^ABC=^ABD (cùng bằng 60o).
Do đó ΔABC=ΔABD (g – c – g).
Khi đó BC = BD = 3,3 cm (2 cạnh tương ứng), AC = AD = 4 cm (2 cạnh tương ứng).
hay a = 3,3 cm; b = 4 cm.
Vậy x=45°; y=60°; a = 3,3 cm; b = 4 cm.
a) ΔOAN=ΔOBM;
b) ΔAMN=ΔBNM.
Lời giải:
a)
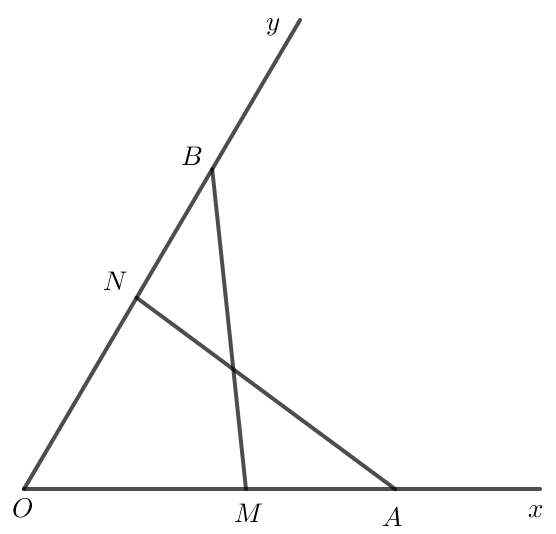
Xét hai tam giác OAN và OBM có:
OA = OB (theo giả thiết).
ˆO chung.
ON = OM (theo giả thiết).
Vậy ΔOAN=ΔOBM (c – g – c).
b)
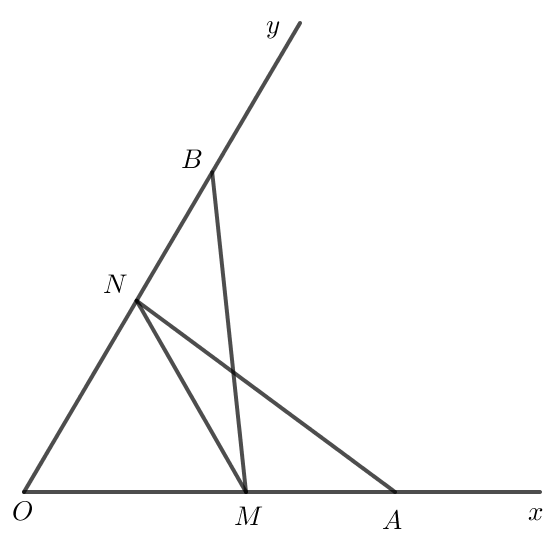
Do ΔOAN=ΔOBM nên AN = BM (2 cạnh tương ứng).
Có BN = OB – ON, AM = OA – OM.
Mà OB = OA, ON = OM nên BN = AM.
Xét hai tam giác AMN và BNM có:
AM = BN (chứng minh trên).
MN chung.
AN = BM (chứng minh trên).
Vậy ΔAMN=ΔBNM (c – c – c).
Bài 4.31 trang 86 Toán 7: Cho Hình 4.74, biết OA = OB, OC = OD. Chứng minh rằng:
a) AC = BD;
b) ΔACD=ΔBDC.
Lời giải:
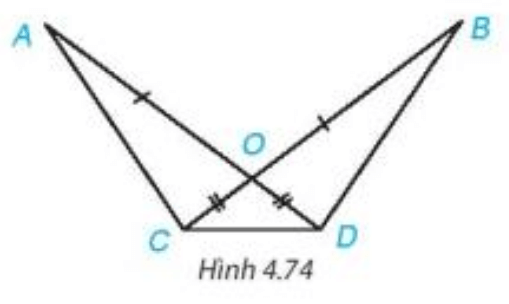
a) Xét hai tam giác AOC và BOD có:
OA = OB (theo giả thiết).
^AOC=^BOD (2 góc đối đỉnh).
OC = OD (theo giả thiết).
Do đó ΔAOC=ΔBOD (c – g – c).
Vậy AC = BD (2 cạnh tương ứng).
b) Có AD = OA + OD, BC = OB + OC.
Mà OA = OB, OC = OD nên AD = BC.
Xét hai tam giác ACD và BDC có:
AD = BC (chứng minh trên).
AC = BD (chứng minh trên).
CD chung.
Vậy ΔACD=ΔBDC (c – c – c).
Lời giải:
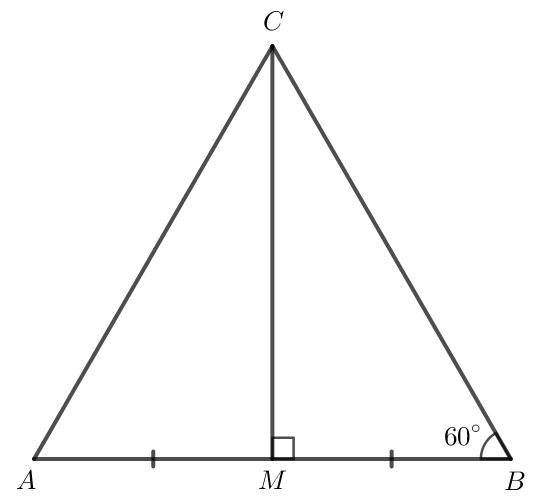Xét hai tam giác AMC vuông tại M và BMC vuông tại M có:
AM = BM (theo giả thiết).
MC chung.
Do đó ΔAMC=ΔBMC (2 cạnh góc vuông).
Khi đó AC = BC (2 cạnh tương ứng).
Tam giác ABC có AC = BC nên tam giác ABC cân tại C.
Tam giác ABC cân tại C lại có ^ABC=60° nên tam giác ABC là tam giác đều.
Vậy tam giác ABC là tam giác đều.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.
