Với giải Bài 3 trang 91 Toán lớp 10 Tập 2 Cánh diều chi tiết trong Bài 5: Phương trình đường tròn giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:
Giải bài tập Toán 10 Bài 3 trang 91 Toán lớp 10 Tập 2
Bài 3 trang 91 Toán lớp 10 Tập 2: Lập phương trình đường tròn trong mỗi trường hợp sau:
a) Đường tròn có tâm O(– 3; 4) và bán kính R = 9;
b) Đường tròn có tâm I(5; – 2) và đi qua điểm M(4; – 1);
c) Đường tròn có tâm I(1; – 1) và có một tiếp tuyến là Δ: 5x – 12y – 1 = 0;
d) Đường tròn đường kính AB với A(3; – 4) và B(– 1; 6);
e) Đường tròn đi qua ba điểm A(1; 1); B(3; 1); C(0; 4).
Lời giải:
a) Phương trình đường tròn có tâm O(– 3; 4) và bán kính R = 9 là
(x – (– 3))2 + (y – 4)2 = 92 hay (x + 3)2 + (y – 4)2 = 81.
b) Đường tròn có tâm I và đi qua điểm M thì có bán kính là
R = IM = .
Vậy phương trình đường tròn cần lập là (x – 5)2 + (y – (– 2))2 = hay (x – 5)2 + ( y + 2)2 = 2.
c) Khoảng cách từ tâm I của đường tròn đến tiếp tuyến ∆ chính bằng bán kính của đường tròn.
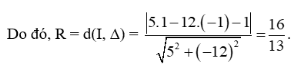
Vậy phương trình đường tròn cần lập là hay .
d) Ta có: AB = .
Gọi I là trung điểm của AB, ta có tọa độ của I là hay I(1; 1).
Đường tròn đường kính AB có tâm là trung điểm I của AB và có bán kính R =
Vậy phương trình đường tròn đường kính AB là (x – 1)2 + (y – 1)2 = 29.
e) Giả sử tâm của đường tròn là điểm I(a; b).
Ta có IA = IB = IC ⇔ IA2 = IB2 = IC2.
Vì IA2 = IB2, IB2 = IC2 nên
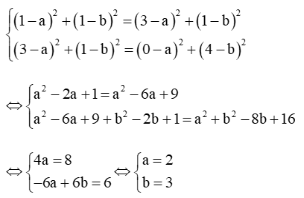
Đường tròn tâm I(2; 3) bán kính R = IC = .
Phương trình đường tròn là .
Vậy phương trình đường tròn là (x – 2)2 + (y – 3)2 = 5.
Xem thêm các bài giải Toán 10 Kết nối tri thức hay, chi tiết khác:
Hoạt động 2 trang 87 Toán lớp 10 Tập 2: Trong mặt phẳng tọa độ Oxy, nêu mối liên hệ giữa x và y để:
Bài 1 trang 91 Toán lớp 10 Tập 2: Phương trình nào sau đây là phương trình đường tròn?
Bài 2 trang 91 Toán lớp 10 Tập 2: Tìm tâm và bán kính của đường tròn trong mỗi trường hợp sau:
Bài 5 trang 92 Toán lớp 10 Tập 2: Tìm m sao cho đường thẳng 3x + 4y + m = 0 tiếp xúc với đường tròn
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.
