Toptailieu.vn xin giới thiệu 40 câu trắc nghiệm Mệnh đề toán học (Cánh diều) có đáp án - Toán 10 chọn lọc, hay nhất giúp học sinh lớp 10 ôn luyện kiến thức để đạt kết quả cao trong các bài thi môn Toán.
Mời các bạn đón xem:
10 câu trắc nghiệm Phương trình đường tròn (Cánh diều) có đáp án - Toán 10
Câu 1: Cho đường tròn (C) có phương trình x2 + y2 + 2x - 8y + 8 = 0. Khi đó đường tròn có tâm I và bán kính R với
A. I(2;-8),R=√17
B. I(1;-4),R=3
C. I(-1;4),R=√17
D. I(1;-4),R=2√2
Đáp án C
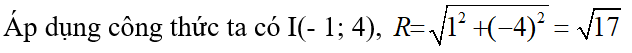
Chú ý: Khi học sinh không nhớ công thức của tâm và bán kính thì cần biến đổi phương trình đường tròn ở dạng tổng quát về dạng chính tắc
x2 + y2 + 2x - 8y = 0 ⟺ (x + 1)2 + (y - 4)2 = 17
Từ đó có thông tin về tâm và bán kính của đường tròn.
Các phương án A, B, D là các sai lầm thường gặp của học sinh.
Câu 2: Điều kiện của m để phương trình
x2 + y2 - 2(m - 3)x - 2(2m + 1)y + 3m + 10 = 0
Là phương trình của một đường tròn là:
A. m ∈ (-∞;0]∪[1;+∞)
B. m ∈ (-∞;0)∪(1;+∞)
C. m ∈ (0;1)
D. m ∈ [0;1]
Đáp án B
Để phương trình x2 + y2 - 2(m - 3)x - 2(2m + 1)y + 3m + 10 = 0 là phương trình của một đường tròn thì (m - 3)2 + (2m + 1)2 - 3m - 10 > 0
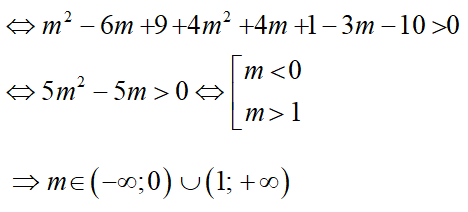
Câu 3: Phương trình đường tròn có tâm I(3; -5) và có bán kính R = 2 là
A. x2+y2+3x-5y+2=0
B. x2+y2+6x-10y+30=0
C. x2+y2-6x+10y-4=0
D. x2+y2-6x+10y+30=0
Đáp án
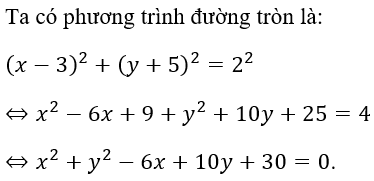
Câu 4: Phương trình đường tròn đường kính AB với A(1; 6), B(-3; 2) là
A. x2 + y2 + 2x - 8y + 9=0
B. x2 + y2 - 2x + 8y + 9=0
D. x2 + y2 + 2x - 8y - 15=0
C. x2 + y2 - 2x + 8y - 15=0
Đáp án A

Câu 5: Phương trình đường tròn đi qua ba điểm A(-1; 3), B(1; 4), C(3; 2) là:
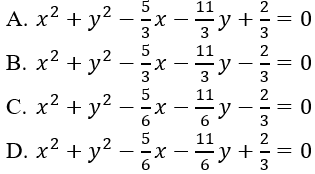
Đáp án B

Chú ý. Học sinh có thể tìm tâm và bán kính trước rồi suy ra phương trình của đường tròn, tuy nhiên cách làm này dài hơn. Khi có phương trình tổng quát của đường tròn rồi thì có ngay thông tin của tâm và bán kính của đường tròn.
Câu 6: Cho đường tròn (C) có tâm nằm trên đường thẳng Δ: x + 2y – 5 = 0 và tiếp xúc với hai đường thẳng d1: 3x-y+5=0 và d2: x+3y-13=0. Khi đó bán kính lớn nhất của đường tròn (C) có thể nhận là:
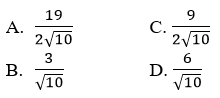
Đáp án
Câu 7: Cho đường tròn (C) có phương trình x2+y2-6x+4y-12=0. Phương trình tiếp tuyến của đường tròn tại điểm A(-1; 1) là:
A. – 4x + 3y – 7 = 0
B. 4x + 3y + 1= 0
C. 3x + 4y – 1 = 0
D. 3x – 4y + 7 = 0
Đáp án D

Câu 8: Cho đường tròn (C) có phương trình x2+y2-6x+4y-12=0 và điểm A(m; 3). Giá trị của m để từ A kẻ được hai tiếp tuyến vuông góc đến (C) là
A. m = 2 hoặc m = 8
B. m = - 2 hoặc m = - 8
C. m = 2 hoặc m = - 8
D. m = - 2 hoặc m = 8
Đáp án D

Câu 9: Cho đường tròn (C) có phương trình (x-2)2+(y+1)2=4. Khi đó đường tròn có tâm I và bán kính R với
A. I(-2; 1), R = 4
B. I(2; -1), R = 4
C. I(2; -1), R = 2
D. I(-2; 1), R = 2
Đáp án C
Đường tròn (C) có phương trình:
(x - 2)2 + (y + 1)2 = 4
Có tâm I(2; -1) và bán kính R = 2.
Câu 10: Cho đường tròn (C) có phương trình x2+y2+4x-6y-3=0. Khi đó đường tròn có tâm I và bán kính R với
A. I(4; -6), R = 4
B. I(-2; 3), R = 16
C. I(-4; 6), R = 4
D. I(-2; 3), R = 4
Đáp án D
Ta có x2+y2+4x-6y-3=0 ⇔ (x+2)2+(y-3)2=16 nên đường tròn có tâm I(-2; 3) và bán kính R = 4.
Chú ý. Học sinh có thể áp dụng công thức tính tâm và bán kính của đường tròn khi biết phương trình tổng quát của đường tròn.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.