Toptailieu.vn biên soạn và giới thiệu Top 20 Đề thi giữa kì 1 Toán 10 (Chân trời sáng tạo 2023) có đáp án gồm các đề thi được tuyển chọn và tổng hợp từ các đề thi môn Toán THPT trên cả nước có hướng dẫn giải chi tiết giúp học sinh làm quen với các dạng đề, ôn luyện để đạt kết quả cao trong kì thi sắp tới. Mời các bạn đón xem:
Nội dung bài viết
Top 20 Đề thi giữa kì 1 Toán 10 (Chân trời sáng tạo 2023) có đáp án
A. MA TRẬN ĐỀ THI GIỮA HỌC KÌ 1 TOÁN 10 CHÂN TRỜI SÁNG TẠO - ĐỀ SỐ 01
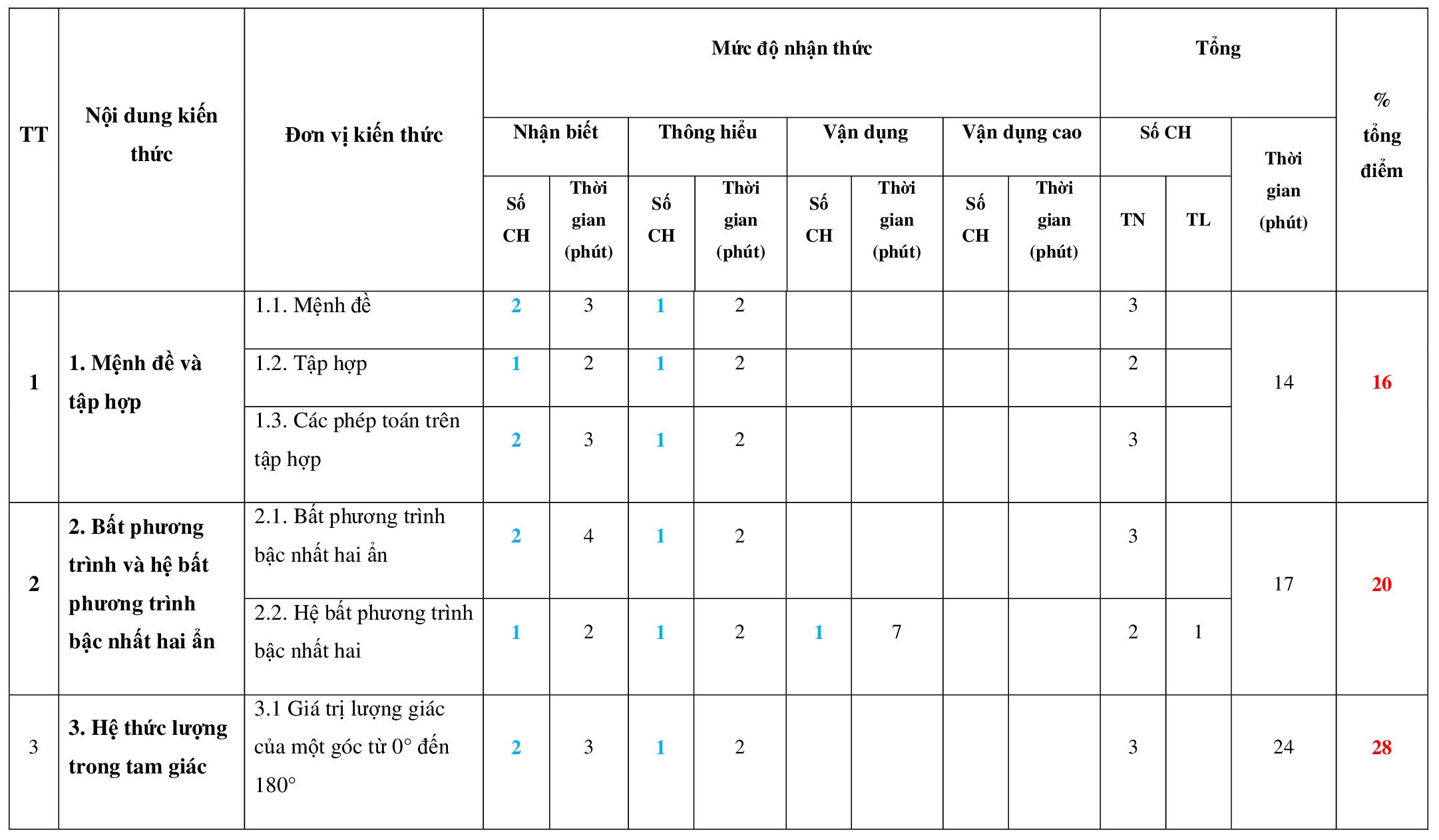
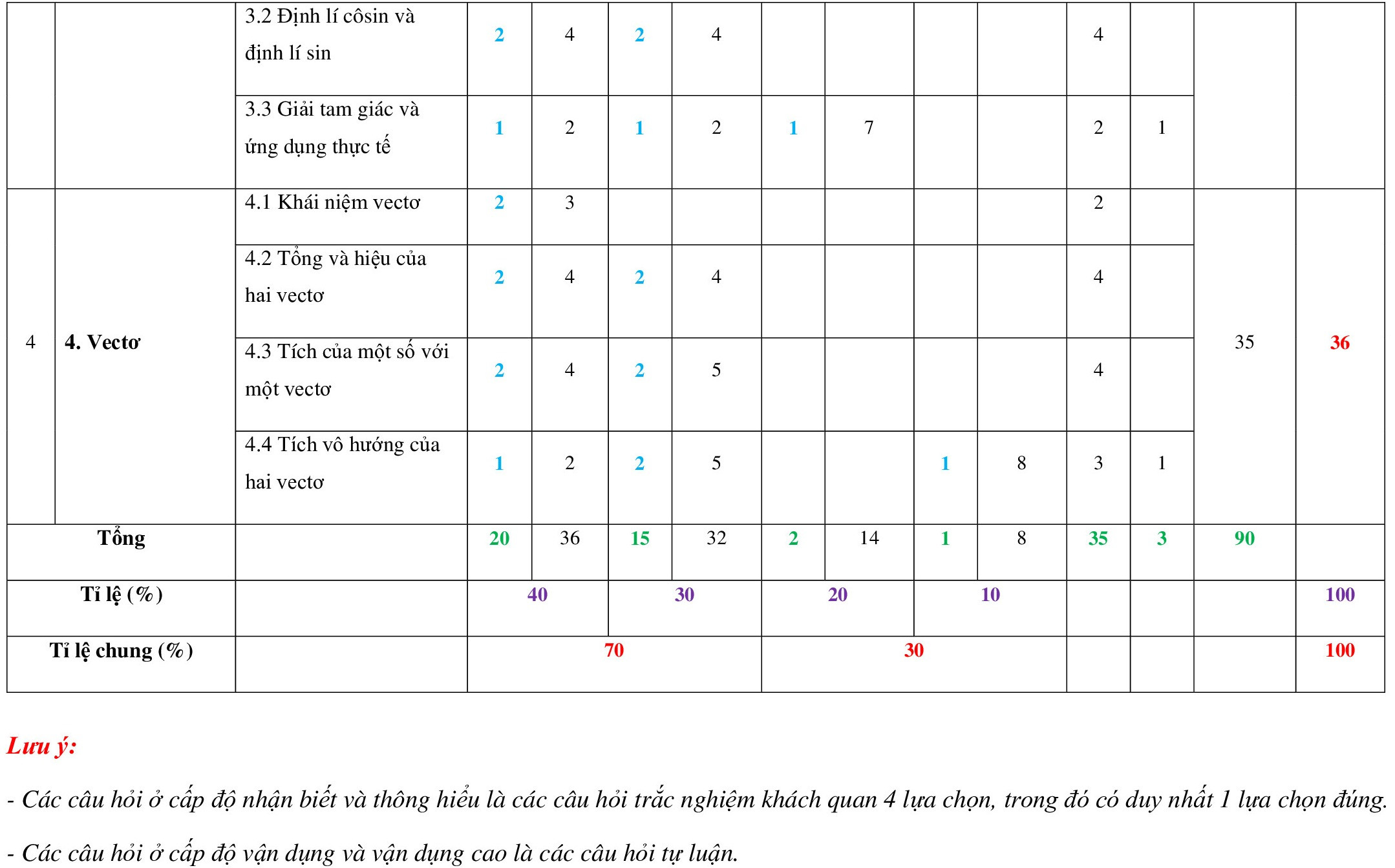
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Giữa Học kì 1
Năm học 2022 - 2023
Môn: Toán 10
Thời gian làm bài: 90 phút
Đề thi Giữa học kì 1 Toán 10 Chân trời sáng tạo (Có đáp án) - Đề số 01
I. Trắc nghiệm (7 điểm)
Câu 1. Cho các câu sau đây:
a) Không được nói chuyện!
b) Ngày mai bạn đi học không?
c) Chủ tịch Hồ Chí Minh sinh năm 1890.
d) 22 chia 3 dư 1.
e) 2005 không là số nguyên tố.
Có bao nhiêu câu là mệnh đề ?
A. 1;
B. 2;
C. 3;
D. 4.
Câu 2. Cho hai mệnh đề P: “x là số chẵn” và Q: “x chia hết cho 2”.
Phát biểu mệnh đề P kéo theo Q.
A. Hoặc x là số chẵn hoặc x chia hết cho 2;
B. Nếu x là số chẵn thì x chia hết cho 2;
C. Nếu x chia hết cho 2 thì x là số chẵn;
D. x là số chẵn và x chia hết cho 2.
Câu 3. Cho tập hợp A là các nghiệm của phương trình x2 – 6x + 5 = 0.
Viết tập hợp trên dưới dạng liệt kê các phần tử.
A. A = {2 ; 3};
B. A = {1 ; 5};
C. A = {4 ; 6};
D. A = {2 ; 4}.
Câu 4. Cho tập hợp H = [1; 7] ∩ (– 3; 5). Đáp án nào sau đây là đúng.
A. H = [1; 7];
B. H = (– 3; 5);
C. H = [1; 5] ;
D. H = [1; 5).
Câu 5. Cho hai tập hợp A = (0; 3), B = (2; 4). Xác định A \ B.
A. A \ B = (0; 2];
B. A \ B = (0; 2);
C. A \ B = (0; 4);
D. A \ B = [3; 4).
Câu 6. Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn ?
A. 2x – 4y + 7 ≥ 0;
B. 5x3 – 4y3 – 2 ≤ 0;
C. x3 – 2y < 0;
D. x2 + 3 > 0.
Câu 7. Cặp số (–1; 3) là một nghiệm của bất phương trình:
A. –3x + 2y – 4 > 0;
B. x + 3y < 0;
C. 3x – y > 0;
D. 2x – y + 4 > 0.
Câu 8. Trong các hệ bất phương trình sau, đâu không là hệ bất phương trình bậc nhất hai ẩn:
A. {x+y≥10x−3y<6;
B. {2x−y−1>0x−2>0x+5y<4;
C. {3x+2y−2<03x−y<4−y5+x2<3;
D. {7x−y<1x+2y<3y−x.
Câu 9. Trong các đẳng thức sau đây, đẳng thức nào đúng?
A. sin60° = √32;
B. cos60° = √32;
C. tan60° = 1;
D. cot60° = −1.
Câu 10. Cho α là góc nhọn. Khẳng định nào sau đây là đúng?
A. sin α < 0;
B. cos α < 0;
C. tan α < 0;
D. cot α > 0.
Câu 11. Chọn đáp án sai: Một tam giác giải được nếu biết:
A. Độ dài 3 cạnh;
B. Độ dài 2 cạnh và 1 góc bất kỳ;
C. Số đo 3 góc;
D. Độ dài 1 cạnh và 2 góc bất kỳ.
Câu 12. Cho hình vuông ABCD tâm O. Giá của vectơ →AO là:
A. Đường thẳng AC;
B. Đường thẳng BC;
C. Đường thẳng AB;
D. Đường thẳng DO.
Câu 13. Cho hình vẽ dưới đây.
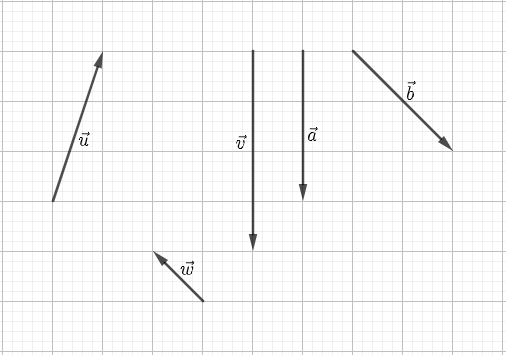
Khẳng định nào sau đây là đúng ?
A. Trong hình có 3 cặp vectơ cùng phương;
B. →u và →w cùng phương;
C. →u và →b cùng phương;
D. →a và →v cùng phương.
Câu 14. Cho 4 điểm A, B, C, D. Ta có: →AB+→BD=?
A. →AC+→BD;
B. →AD+→DB;
C. →AC+→CD;
D. →DA+→DB.
Cau 15. Cho hình vuông ABCD tâm O. Khi đó, →OA−→OB=?
A. →CD;
B. →AB;
C. →AC;
D. →BD.
Câu 16. Cho tam giác đều ABC cạnh 4. Vectơ −12→BC có độ dài là.
A. 2;
B. 4;
C. 3;
D. 6.
Câu 17. Cho tam giác ABC có a = 4, b = 6 và cosC = 23. Giá trị của c bằng:
A. 3√5;
B. 2√5;
C. 5√2;
D. 5√3.
Câu 18. Cho →a và →b không cùng phương và hai vectơ →x=2→a+→b và →y=−4→a−2→b. Khẳng định nào sau đây là đúng ?
A. →x và →y cùng phương, cùng hướng;
B. →x và →y không cùng phương;
C. →x và →y bằng nhau;
D. →x và →y cùng phương, ngược hướng.
Câu 19. Cho tam giác ABC có ˆA=60°, , b = 4. Tính cạnh a.
A. ;
B. ;
C. ;
D. .
Câu 20. Cho hai vectơ và cùng khác . Công thức tính tích vô hướng của hai vectơ là:
A. ;
B. ;
C. ;
D. .
Câu 21. Phần tô đậm trong hình vẽ sau biểu diễn tập nghiệm của bất phương trình nào trong các bất phương trình sau?
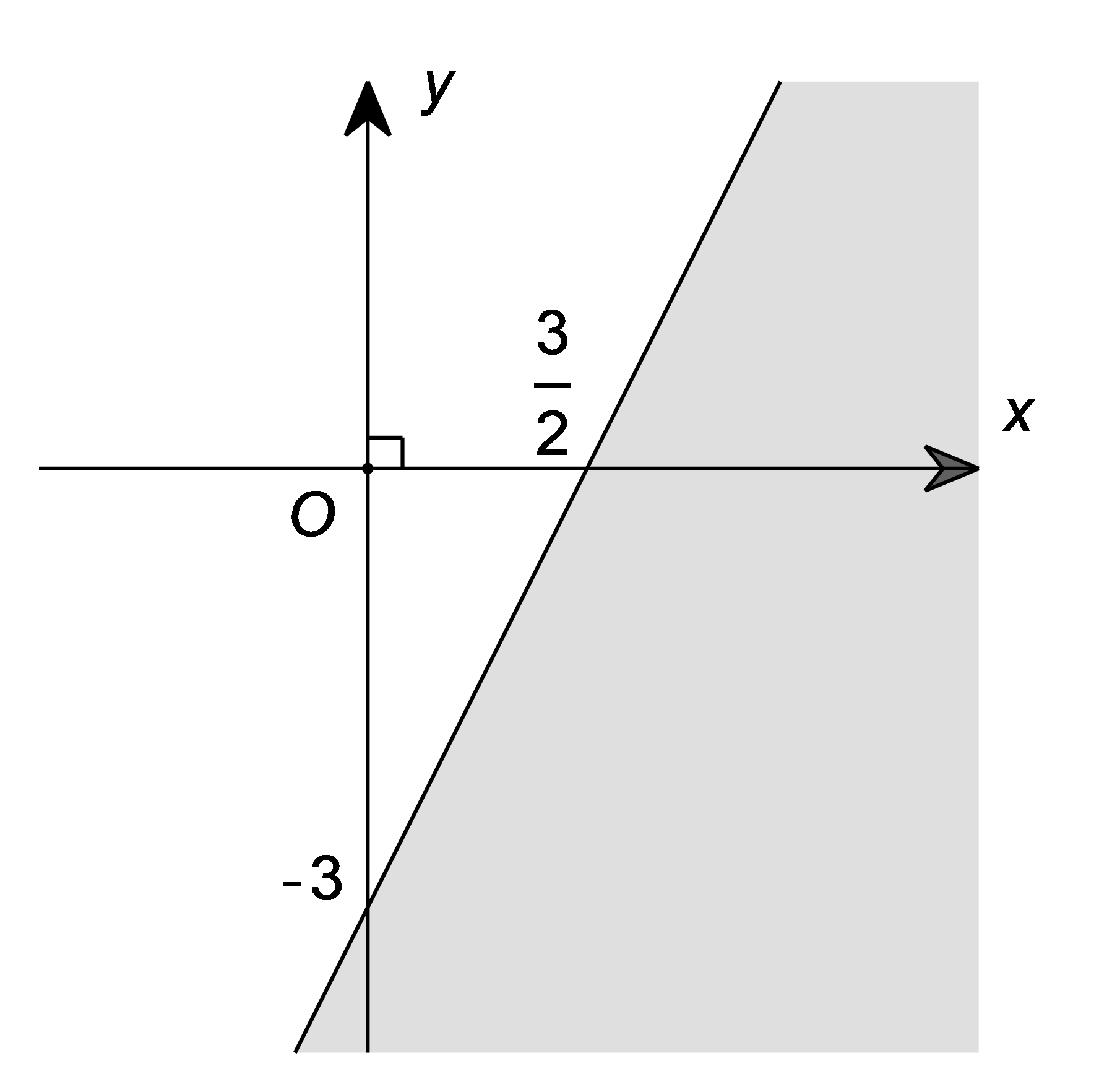
A. 2x – y < 3;
B. 2x – y > 3;
C. x – 2y < 3;
D. x – 2y > 3.
Câu 22. Biết tam giác ABC có a = 16, b = 17, c = 20. Chọn phương án có kết quả đúng nhất?
A. = 55,45°; ; ;
B. = 50,45°; ; ;
C. = 50,45°; ; ;
D. = 55,45°; ; .
Câu 23. Mệnh đề nào dưới đây có mệnh đề phủ định của nó là đúng?
B. “∀n ∈ ℕ: 3n ≥ n”;
C. “∃x ∈ ℚ: x2 = 5”;
D. “∃x ∈ ℝ: x2 – 3 = 2x”.
Câu 24. Cho hình chữ nhật ABCD tâm O có: AD = a, AB = 2a. Tính
A. a;
B. 0;
C. a2;
D. 2a2.
Câu 25. Cho tam giác ABC vuông cân tại C và AB = . Tính .
A. 3;
B. 1;
C. 2;
D. 4.
Câu 26. Biết sin α + cos α = . Giá trị của biểu thức Q = sin4α – cos4α là:
A. 1;
B. – 1;
C. 0;
D. 2.
Câu 27. Cho A = (– ∞; – 2], B = [3; + ∞), C = (0; 4). Khi đó tập (A ∪ B) ∩ C là:
A. [3; 4];
B. (– ∞; – 2] ∪ (3; + ∞);
C. [3; 4);
D. (– ∞; – 2) ∪ [3; + ∞).
Câu 28. Cho hình bình hành ABCD và điểm M, biết . Điểm M là:
A. Điểm thuộc đường tròn tâm A, bán kính AC;
B. Điểm thuộc đường tròn tâm A, bán kính BD;
C. Điểm thuộc đường tròn tâm B, bán kính AC;
D. Điểm thuộc đường tròn tâm B, bán kính BD.
Câu 29. Tam giác DEF có DE = 5, DF = 8 và . Bán kính r của đường tròn nội tiếp tam giác đã cho gần nhất với giá trị nào sau đây?
A. 1,5;
B. 15;
C. 2;
D. 20.
Câu 30. Cho hai điểm A, B và O là trung điểm của AB. Gọi M là một điểm tùy ý, khẳng định nào sau đây là đúng ?
A. ;
B. ;
C. ;
D. .
Câu 31. Cho tam giác ABC. Đặt , . M thuộc cạnh AB sao cho AB = 3AM, N thuộc tia BC và CN = 2BC. Phân tích qua các vectơ và ta được biểu thức là:
A. ;
B. ;
C. ;
D. .
Câu 32. Tam giác đều nội tiếp đường tròn bán kính R = 8 cm có diện tích là:
A. 12;
B. 24;
C. 48;
D. 6.
Câu 33. Cho tập hợp H = (– ∞; 3) ∪ [9; + ∞). Hãy viết lại tập hợp H dưới dạng nêu tính chất đặc trưng.
A. H = {x ∈ ℝ| x < 3 hoặc x ≥ 9};
B. H = {x ∈ ℝ| x ≥ 9};
C. H = {x ∈ ℝ| x < 3};
D. H = {x ∈ ℝ| 3 < x ≤ 9};
Câu 34. Phần không tô đậm trong hình vẽ dưới đây (không chứa biên) biểu diễn tập nghiệm của hệ bất phương trình nào trong các hệ bất phương trình sau?
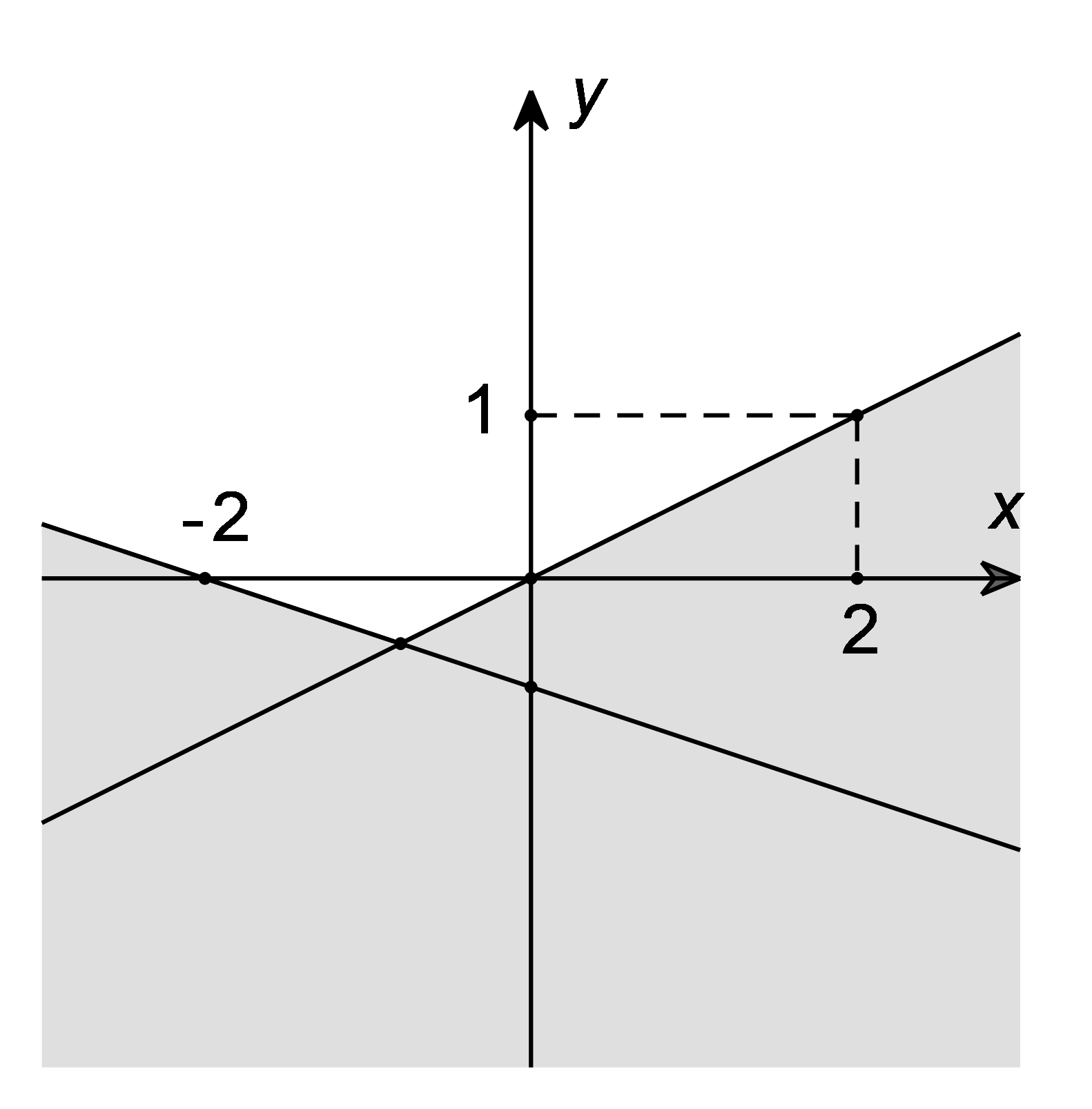
A. ;
B. ;
C. ;
D. .
Câu 35. Cho tứ giác ABCD. Gọi E, F lần lượt là trung điểm của AB, CD, O là trung điểm của EF. Khẳng định nào sau đây là đúng ?
A. ;
B. ;
C. ;
D. .
II. Tự luận (3 điểm)
Câu 1. Để làm đường điện dây cao thế ở Hà Giang từ vị trí bản A đến bản B, người ta phải tránh một ngọn núi nên người ta phải nối thẳng đường dây từ bản A đến bản C dài 12 km rồi nối từ bản C đến bản B dài 8 km. Qua đo đạc người ta xác định được . Hỏi so với việc nối thẳng từ bản A đến bản B, người ta tốn thêm bao nhiêu tiền, biết mỗi km dây có giá 150 000 đồng.
Câu 2. Một nông dân định trồng đậu và cà trên diện tích 8 ha. Nếu trồng đậu thì cần 20 công và thu 3 000 000 đồng trên diện tích mỗi ha, nếu trồng cà thì cần 30 công và thu 4 000 000 đồng trên diện tích mỗi ha. Hỏi cần trồng mỗi loại cây trên với diện tích là bao nhiêu để thu được nhiều tiền nhất biết rằng tổng số công không quá 180 ?
Câu 3. Một vật chịu tác động của hai lực bao gồm theo phương tạo với phương nằm ngang một góc 60° và theo phương nằm ngang. Vật di chuyển được một đoạn 4 m theo phương ngang từ M. Hai lực và có cùng độ lớn bằng 10 N. Công sinh bởi hợp lực của và có độ lớn bằng bao nhiêu?
Đáp án Đề thi Giữa học kì 1 Toán 10 Chân trời sáng tạo - Đề số 01
I. Bảng đáp án trắc nghiệm
|
1. C |
2. B |
3. B |
4. D |
5. A |
6. A |
7. A |
|
8. C |
9. A |
10. D |
11. C |
12. A |
13. D |
14. C |
|
15. A |
16. A |
17. B |
18. D |
19. A |
20. B |
21. B |
|
22. B |
23. C |
24. D |
25. B |
26. C |
27. C |
28. A |
|
29. A |
30. A |
31. A |
32. C |
33. A |
34. D |
35. D |
II. Lời giải chi tiết trắc nghiệm
Câu 1.
Đáp án đúng là: C
a) Câu a) không phải là mệnh đề vì nó là câu mệnh lệnh và không khẳng định tính đúng sai.
b) Câu b) không phải là mệnh đề vì nó là câu hỏi và không khẳng định tính đúng sai.
c) Câu c) là mệnh đề vì đó là câu khẳng định tính đúng sai.
d) Câu d) là mệnh đề vì đó là câu khẳng định tính đúng sai.
e) Câu e) là mệnh đề vì đó là câu khẳng định tính đúng sai.
Vậy có 3 câu là mệnh đề.
Câu 2.
Đáp án đúng là: B
Vì mệnh đề kéo theo được phát biểu dưới dạng là “Nếu P thì Q”.
Nên mệnh đề P kéo theo Q là “Nếu x là số chẵn thì x chia hết cho 2”.
Câu 3.
Đáp án đúng là: B
Ta có x2 – 6x + 5 = 0 ⇔ x = 1 hoặc x = 5.
Do đó tập hợp A gồm hai phần tử là 1 và 5.
Vậy A = {1 ; 5}.
Câu 4.
Đáp án đúng là: D
Ta biểu diễn đoạn [1; 7] và khoảng (– 3; 5) lên cùng một trục số, giao của hai tập này chính là phần không bị gạch chéo trên hình sau. Chú ý các điểm đặc biệt ở mút 1 và 5.
![]()
Vậy H = [1; 7] ∩ (– 3; 5) = [1; 5).
Câu 5.
Đáp án đúng là: A
– Biểu diễn tập hợp A trên trục số ta có:

– Biểu diễn tập hợp B trên trục số ta có:

Vì hiệu của tập hợp A và B là các phần tử thuộc A nhưng không thuộc B.
Mà nhìn vào trục số trên ta thấy nửa khoảng (0; 2] thuộc tập hợp A, không thuộc tập hợp B do đó hiệu của A và B gồm các phần tử nằm trong nửa khoảng (0; 2].
Vậy A \ B = (0; 2].
Câu 6.
Đáp án đúng là: A
Trong các bất phương trình đã cho ta thấy bất phương trình ở đáp án A là bất phương trình bậc nhất hai ẩn do bậc của ẩn x và y đều là 1 và hệ số của x và y không đồng thời bằng 0.
Đáp án B không thỏa mãn do bậc của x và y là 3, đáp án C không thỏa mãn do bậc của x là 3 và đáp án D không thỏa mãn do bậc của x là 2.
Câu 7.
Đáp án đúng là: A
Xét cặp số (–1; 3) và bất phương trình: –3x + 2y – 4 > 0 ta có:
–3.(–1) + 2.3 – 4 = 5 > 0
Do đó, cặp số (–1; 3) là một nghiệm của bất phương trình: –3x + 2y – 4 > 0.
Câu 8.
Đáp án đúng là: C
Xét hệ ta có: 5 + x2 < 3 có bậc của x là 2 nên đây không là một bất phương trình bậc nhất hai ẩn.
Do đó, hệ không là hệ bất phương trình bậc nhất hai ẩn.
Câu 9.
Đáp án đúng là: A
Theo bảng giá trị lượng giác của một số góc đặc biệt (hoặc dùng máy tính cầm tay), ta có: sin60° = ; cos60° = ; tan60° =; cot60° =.
Vậy đáp án A đúng.
Câu 10.
Đáp án đúng là: D
Vì α là góc nhọn nên sin α > 0, cos α > 0, tan α > 0, cot α > 0.
Vậy A, B, C sai và D đúng.
Câu 11.
Đáp án đúng là: C
Một tam giác giải được khi ta biết 3 yếu tố của nó, trong đó phải có ít nhất một yếu tố độ dài (tức là yếu tố góc không được quá 2).
Vậy đáp án C là đáp án sai.
Câu 12.
Đáp án đúng là: A
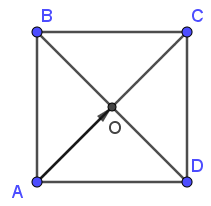
Giá của vectơ là đường thẳng đi qua hai điểm A và O, đó là đường thẳng AO hay chính là đường thẳng AC do O là tâm của hình vuông.
Câu 13.
Đáp án đúng là: D
Từ hình vẽ ta có:
+) và có giá song song với nhau nên và cùng phương.
+) và có giá song song với nhau nên và cùng phương.
Vậy trong hình có hai cặp vectơ cùng phương.
Do đó ta chọn đáp án D.
Câu 14.
Đáp án đúng là: C
Áp dụng quy tắc ba điểm cho ba điểm A, D, B ta có: .
Áp dụng quy tắc ba điểm cho ba điểm A, D, C ta có: .
Vậy .
Câu 15.
Đáp án đúng là: A
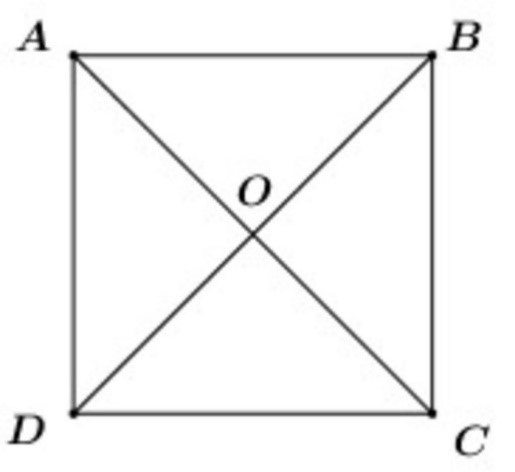
Xét 3 điểm A, O, B có:
Do ABCD là hình vuông nên ta có:
Vậy .
Câu 16.
Đáp án đúng là: A
Do tam giác ABC đều cạnh 4 nên: AB = AC = BC = 4
⇒ = 4
Ta có: .
Câu 17.
Đáp án đúng là: B
Áp dụng định lý côsin vào tam giác ABC ta có:
Thay số
.
Do đó: .
Câu 18.
Đáp án đúng là: D
Ta có:
Vì – 2 < 0
Do đó, và cùng phương, ngược hướng.
Câu 19.
Đáp án đúng là: A
Theo định lí sin ta có
.
Câu 20.
Đáp án đúng là: B
Công thức tính tích vô hướng của hai vectơ và là: .
Câu 21.
Đáp án đúng là: B
Đường thẳng đi qua hai điểm và B(0; – 3) nên có phương trình 2x – y = 3.
Mặt khác, cặp số (0; 0) không thỏa mãn bất phương trình 2x – y > 3 nên phần tô đậm ở hình trên biểu diễn miền nghiệm của bất phương trình 2x – y > 3.
Câu 22.
Đáp án đúng là: B
Ta có: cos A =
= 50,45![]() .
.
Tương tự: cos B =
Do đó:
.
Câu 23.
Đáp án đúng là: C
Mệnh đề phủ định của các mệnh đề đã cho là:
+ : “∃x ∈ ℝ: x ≥ x + 2”
Mệnh đề này sai vì:
Ta giả sử thay x = 0 vào bất phương trình x ≥ x + 2.
⇒ 0 ≥ 2 (vô lý).
+ : “∃n ∈ ℕ: 3n < n”
Mệnh đề này sai vì:
∀n ∈ ℕ: 3 ≥ 1 ⇒ 3n ≥ n.
+ : “∀x ∈ ℚ: x2 ≠ 5”
Mệnh đề này đúng vì:
x2 = 5 ⇔ x = ± ∉ ℚ.
+ : “∀x ∈ ℝ: x2 – 3 ≠ 2x”
Mệnh đề này sai vì:
x2 – 3 = 2x ⇔ x2 – 2x – 3 = 0
Mà phương trình x2 – 2x – 3 = 0 có hai nghiệm phân biệt là –1 và 3 nên có tồn tại số thực x để x2 – 3 = 2x.
Câu 24.
Đáp án đúng là: D
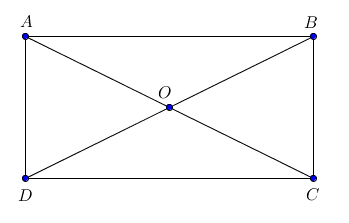
Do ABCD là hình chữ nhật nên ta có: BC = AD = a, AB = CD = 2a.
Xét tam giác ABC vuông tại B
Áp dụng định lí Pythagore ta có:
AC2 = AB2 + BC2 = (2a)2 + a2 = 5a2
⇒ AC = a
Ta có:
Suy ra
Ta có: .
Câu 25.
Đáp án đúng là: B
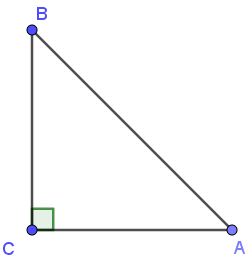
Ta có: .
Xét tam giác ABC vuông tại C
Áp dụng định lý Pythagore ta có:
AB2 = BC2 + CA2
Mà BC = CA nên BC2 = CA2 = ==1
⇔ CB = CA = 1
Vậy = CB = 1.
Câu 26.
Đáp án đúng là: C
Ta có: Q = sin4α – cos4α = (sin2α + cos2α) . (sin2α – cos2α)
= 1 . (sinα – cosα) . (sinα + cosα)
= (sinα – cosα).
Mặt khác: sin α + cos α = ⇒ (sin α + cos α)2 = 2
⇔ sin2α + 2 sin α . cos α + cos2α = 2
⇔ (sin2α + cos2α) + 2 sin α . cos α = 2
⇔ 1 + 2 sin α . cos α = 2
.
Do đó: (sinα – cosα)2 = sin2α + cos2α – 2.sinα.cosα = 1 – 2 . = 0.
Suy ra: sin α – cos α = 0.
Vậy Q = 0.
Câu 27.
Đáp án đúng là: C
Ta có: A ∪ B = (– ∞; – 2) ∪ [3; + ∞)
(A ∪ B) ∩ C = (– ∞; – 2) ∪ [3; + ∞) ∩ (0; 4) = [3; 4).
Câu 28.
Đáp án đúng là: A
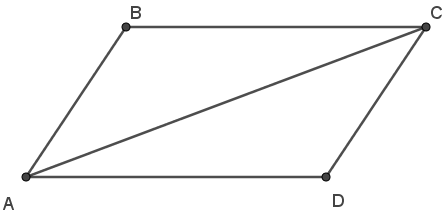
Xét hình bình hành ABCD có: .
Ta có: .
Do A, C cố định nên cố định là một số thực.
Vậy M là điểm thuộc đường tròn tâm A bán kính AC.
Câu 29.
Đáp án đúng là: A
Theo định lí côsin ta có:
Ta có .
Do đó diện tích tam giác ABC là:
.
Lại có .
Câu 30.
Đáp án đúng là: A
Do O là trung điểm AB nên và OA = OB, hai vectơ ngược hướng, do đó .
Ta có:
(quy tắc ba điểm)
.
Câu 31.
Đáp án đúng là: A
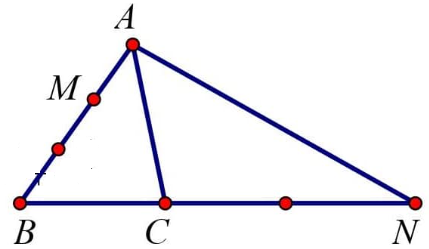
Theo đề bài:
AB = 3AM nên
CN = 2BC nên
Ta có:
.
Câu 32.
Đáp án đúng là: C
Giả sử tam giác ABC đều nội tiếp đường tròn bán kính R = 8 cm.
Do tam giác ABC đều nên ta có
Sử dụng công thức định lý sin:
⇒ a = 2R . sinA = 2 . 8 . sin60° =
Do tam giác ABC đều nên ta có a = b và , áp dụng công thức ta có diện tích tam giác là S = .
Câu 33.
Đáp án đúng là: A
Ta có: A = (– ∞; 3) = {x ∈ ℝ| x < 3}
B = [9; + ∞) = {x ∈ ℝ| x ≥ 9}
Mà H = A ∪ B = {x | x ∈ A hoặc x ∈ B}.
Do đó, H = {x ∈ ℝ| x < 3 hoặc x ≥ 9}.
Câu 34.
Đáp án đúng là: D
Do miền nghiệm không chứa biên nên ta loại đáp án A và C.
Chọn điểm có tọa độ (0; 1) thuộc phần không tô đậm thử vào các hệ bất phương trình.
Xét đáp án B, ta có : Sai.
Xét đáp án D, ta có : Đúng.
Vậy ta chọn đáp án D.
Câu 35.
Đáp án đúng là: D
Ta có:
(do E, F lần lượt là trung điểm của AB, CD)
(do O là trung điểm của EF)
Do đó, ta có:
(quy tắc ba điểm)
.
Vậy .
III. Lời giải tự luận
Câu 1.
Ta mô phỏng bài toán như hình vẽ sau:
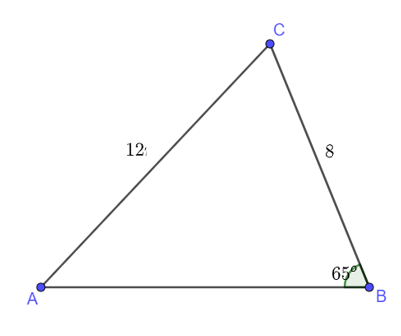
Áp dụng định lí côsin ta có:
Do đó: AB = 13 km.
Ta có: AC + BC – AB = 12 + 8 – 13 = 7 (km)
Vậy số tiền phải tốn thêm 7 . 150 000 = 1 050 000 (đồng).
Câu 2.
Gọi số ha đậu và cà mà hộ nông dân này trồng lần lượt là x và y (x, y ≥ 0).
Lợi nhuận thu được là F(x; y) = 3 000 000x + 4 000 000y (đồng).
Tổng số công dùng để trồng x ha đậu và y ha cà là 20x + 30y.
Ta có hệ bất phương trình:
Miền nghiệm của hệ bất phương trình trên là miền tứ giác không bị gạch chéo trong hình vẽ (kể cả biên).
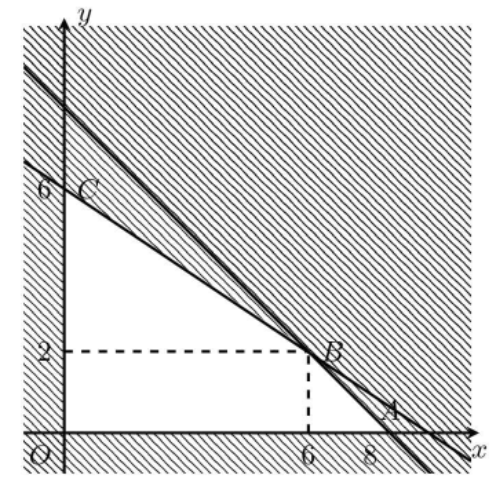
F(x; y) đạt giá trị lớn nhất khi (x; y) là tọa độ của một trong các đỉnh của tứ giác.
Ta có:
F(0; 0) = 0
F(8; 0) = 24 000 000
F(6; 2) = 26 000 000
F(0; 6) = 24 000 000
Suy ra F(x; y) lớn nhất khi (x; y) = (6; 2) tức là hộ nông dân này cần phải trồng 6 ha đậu và 2 ha cà thì sẽ thu về lợi nhuận lớn nhất.
Câu 3.
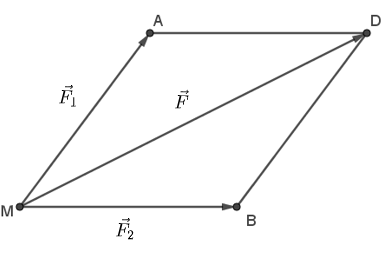
Ta có:
Theo quy tắc hình bình hành ta có: .
Xét hình bình hành ADBM có:
MA = MB,
Do đó, ADBM là hình thoi.
Nên đường chéo MD là tia phân giác của góc AMB.
.
Góc giữa hợp lực (theo phương ) và hướng dịch chuyển là .
.
Ta có:
Do đó,
Vậy độ lớn của hợp lực của và là N.
Công sinh bởi hợp lực của và là:
(J).
B. MA TRẬN ĐỀ THI GIỮA HỌC KÌ 1 TOÁN 10 CHÂN TRỜI SÁNG TẠO - ĐỀ SỐ 02
(30 câu – TN – 6 điểm, 5 câu – TL – 4 điểm)
|
TT |
Nội dung/bài/chủ đề |
Mức độ |
Số câu |
Ghi chú |
||||
|
Nhận biết |
Thông hiểu |
Vận dụng |
Vận dụng cao |
TN |
TL |
|||
|
1 |
Mệnh đề toán học |
2 |
1 |
|
|
3 |
|
0,6 điểm |
|
2 |
Tập hợp và các phép toán trên tập hợp |
2 |
3 |
2 |
|
6 |
1 |
2,2 điểm |
|
3 |
Bất phương trình bậc nhất hai ẩn |
1 |
|
1 |
|
2 |
|
0,4 điểm |
|
4 |
Hệ bất phương trình bậc nhất hai ẩn |
|
1 |
|
1 |
1 |
1 |
1,2 điểm |
|
5 |
Giá trị lượng giác của góc từ 00 đến 1800 |
2 |
1 |
1 |
|
4 |
|
0,8 điểm |
|
6 |
Định lí cosin và định lí sin. Giải tam giác |
1 |
2 |
1 |
1 |
4 |
1 |
1,8 điểm |
|
7 |
Khái niệm vectơ |
2 |
1 |
|
|
3 |
|
0,6 điểm |
|
8 |
Tổng, hiệu của các vectơ. |
1 |
1 |
1 |
1 |
3 |
1 |
1,6 điểm |
|
9 |
Tích của một vectơ với một số. |
1 |
1 |
1 |
1 |
4 |
|
0,8 điểm |
|
|
Tổng số |
|
|
|
|
0,2x30 = 6 điểm |
1x4 =4 điểm |
10 điểm |
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Giữa Học kì 1
Năm học 2022 - 2023
Môn: Toán 10
Thời gian làm bài: 90 phút
Đề thi Giữa học kì 1 Toán 10 Chân trời sáng tạo (Có đáp án) - Đề số 02
I. TRẮC NGHIỆM( 7 điểm)
Câu 1: Trong các bất phương trình dưới đây, bất phương trình nào là bất phương trình bậc nhất hai ẩn?
A. 0x + 7y > 9 + 7y;
B. ;
C. x2 – 2y < 0;
D. x + 0.y2 ≥ 5 – y.
Câu 2: Cho , . Tập hợp là:
A. [0; 5].
B. ℝ;
C. (0; 5);
D. (0; 5].
Câu 3: Cho tam giác ABC có sinA = . Tính sin(B + C).
A. sin(B + C) = ;
B. sin(B + C) = ;
C. sin(B + C) = ;
D. sin(B + C) = .
Câu 4: Tính giá trị biểu thức sau: M = sin75° + tan45° + cos165°.
A. M = 1;
B. M = 2;
C. M = 0;
D. M = – 1.
Câu 5: Cho hình thoi ABCD có góc cạnh 2a. Gọi O là giao điểm của hai đường chéo. Mệnh đề nào sau đây sai?
A. ;
B. ;
C. ;
D. .
Câu 6: Cho tam giác ABC với M là trung điểm của BC. Mệnh đề nào sau đây là đúng?
A. ;
B. ;
C. ;
D. .
Câu 7: Cho hình bình hành ABCD, có AB = 4, BC = 5, BD = 7. Độ dài của AC gần nhất với giá trị nào sau đây:
A. 7,0;
B. 5,9;
C. 5,7;
D. 7,5.
Câu 8: Cho hình bình hành ABCD . Mệnh đề nào sau đây là đúng?
A. ;
B. ;
C. ;
D. .
Câu 9: Cho tập M = {1; 2; 3; 4; 5} và tập N = {3; 4; 5}. Số các tập X có 4 phần tử thỏa mãn N ⊂ X ⊂ M là :
A. 1;
B. 2;
C. 3;
D. 4.
Câu 10: Cho tam giác ABC có AB = 6, . Độ dài cạnh BC là:
A. BC ≈ 8,4;
B. BC ≈ 4,3;
C. BC ≈ 7,0;
D. BC ≈ 5,2.
Câu 11: Gọi D là tập xác định của hàm số . Tìm tập hợp ℝ\D:
A. ℝ\D = [– 2; +∞) \ {3};
B. ℝ\D = (– ∞; – 2);
C. ℝ\D = (– ∞; – 2) \ {– 4};
D. ℝ\D = [– 2; +∞) \ {– 4}.
Câu 12: Trong các câu sau, câu nào không phải là mệnh đề ?
A. Hôm nay trời mưa to quá!;
B. Hà Nội là thủ đô của nước Việt Nam;
C. là số vô tỉ;
D. 6 là số nguyên tố.
Câu 13: Cặp số nào sau đây không là nghiệm của hệ bất phương trình
A. (0; 0);
B. (1; 1);
C. (– 1; 1);
D. (– 1; – 1).
Câu 14: Cho tam giác đều ABC có cạnh bằng 1. Giá trị bằng bao nhiêu?
A. ;
B. ;
C. ;
D. .
Câu 15: Cho A = {x ∈ ℕ| x chia hết cho 3 và x chia hết cho 2}, B = {x ∈ ℕ| x chia hết cho 12}. Nhận xét nào dưới đây là đúng?
A. A ⊂ B;
B. B ⊂ A;
C. A = B;
D. Các đáp án A, B, C đều sai.
Câu 16: Miền nghiệm của hệ bất phương trình là:
A. miền trong tam giác OAB với A(2; 0), B(0; 1) và O (0; 0);
B. miền trong tứ giác OMNP với O(0; 0), M(2; 0), N(0; 1) và P(– 2; 2);
C. nửa mặt phẳng giới hạn bởi các đường thẳng Ox, Oy và đường thẳng x + 2y = 2;
D. nửa mặt phẳng bờ là đường thẳng x + 2y = 2 không chứa gốc tọa độ O(0; 0).
Câu 17: Với tam giác ABC có bao nhiêu vectơ khác vectơ - không có điểm đầu và điểm cuối là ba đỉnh của tam giác?
A. 6.
B. 4.
C. 5.
D. 3.
Câu 18: Các phần tử của tập hợp A = {x ∈ ℝ: 2x2 – 5x – 7 = 0} là:
A. .
B. .
C. .
D. .
Câu 19: Cho các điểm phân biệt A, B, C, D. Đẳng thức nào sau đây đúng ?
A. .
B. .
C. .
D. .
Câu 20: Cho tam giác ABC có BC = 24, AC = 13, AB = 15. Nhận xét nào sau đây đúng về tam giác ABC.
A. ABC là tam giác tù, với ;
B. ABC là tam giác vuông tại A;
C. ABC là tam giác nhọn;
D. ABC là tam giác tù, với .
Câu 21: Xét mệnh đề P: “∃ x ∈ ℝ: 2x – 3 ≥ 0”. Mệnh đề phủ định của mệnh đề P là
A. “∃ x ∈ ℝ: 2x – 3 ≥ 0”;
B. “∀ x ∈ ℝ: 2x – 3 < 0”;
C. “∀ x ∈ ℝ: 2x – 3 ≤ 0”;
D. “∃ x ∈ ℝ: 2x – 3 > 0”.
II. TỰ LUẬN( 3 ĐIỂM)
Bài 1. (1 điểm)
a) Cho các tập hợp A = {0; 1; 2; 3; 4; 5} và B = {2; 3; 4; 5; 6}. Tìm các tập hợp A ∪ B, A ∩ B.
b) Tìm m để A = (m – 1; 2] là tập con của tập B = (0; m + 9).
Bài 2.(1 điểm) Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức F(x; y) = 5x – 10y với cặp (x; y) thuộc vào miền nghiệm của hệ bất phương trình .
Bài 3. (1 điểm)
a) (0,5 điểm) Cho tứ giác MNPQ. Gọi H, K lần lượt là trung điểm của MN và PQ. Chứng minh rằng .
b) (0,5 điểm) Cho hai điểm A, B. Tìm tập hợp điểm M thỏa mãn .
Đáp án đề thi Giữa học kì 1 Toán 10 Chân trời sáng tạo - Đề số 02
I. ĐÁP ÁN TRẮC NGHIỆM
| 1.D | 2.D | 3.C | 4.D | 5.B | 6.C | 7.C |
| 8.A | 9.B | 10.D | 11.D | 12.A | 13.B | 14.C |
| 15.A | 16.A | 17.A | 18.C | 19.C | 20.D | 21.B |
Câu 1:
Hướng dẫn giải
Đáp án đúng là D
Bất phương trình bậc nhất hai ẩn có dạng ax + by ≥ c (ax + by > c; ax + by < c; ax + by ≤ c) trong đó a, b, c là những hệ số cho trước; a, b không đồng thời bằng 0 và x, y là các ẩn. Khi đó ta có:
0x + 7y < 9 + 7y ⇔ 0x + 0y < 9 không là bất phương trình bậc nhất hai ẩn vì a và b đồng thời bằng 0.
không có dạng của bất phương trình bậc nhất hai ẩn.
x2 – 2y < 0 là bất phương trình bậc hai.
x + 0.y2 ≥ 5 – y ⇔ x + y ≥ 5 là bất phương trình bậc nhất hai ẩn với a = , b = 1 và c = 5.
Câu 2:
Hướng dẫn giải
Đáp án đúng là: D
Ta biểu diễn các tập hợp trên trục số như sau:
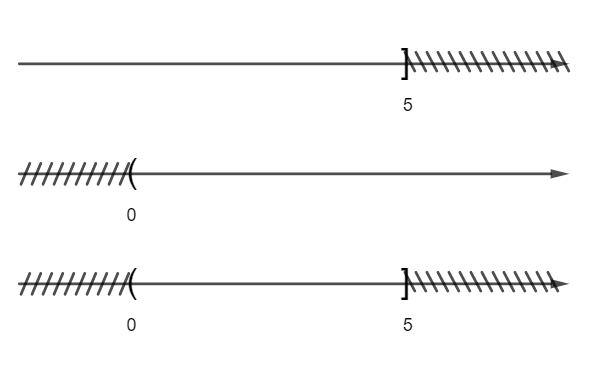
Vậy A ∩ B = (0; 5].
Câu 3:
Hướng dẫn giải
Đáp án đúng là: A
Xét tam giác ABC, có:
sin(B + C) = sin(180° – A) = sinA = .
Câu 4:
Hướng dẫn giải
Đáp án đúng là: A
M = sin75° + tan45° + cos165°
= sin75° + 1 + cos(180° – 15°)
= sin75° + 1 – cos15°
= sin75° + 1 – cos(90° – 75°)
= sin75° + 1 – sin75°
= 1.
Câu 5:
Hướng dẫn giải
Đáp án đúng là: B
Xét tam giác ABD, có AB = AD = 2a nên tam giác ABC cân tại A.
Ta lại có: nên ABC là tam giác đều.
Do đó AO =
Vì ABCD là hình thoi nên CO = AO = , AC = .
Ta có:
. Do đó A đúng.
. Do đó B sai.
. Do đó C đúng.
. Do đó D đúng.
Câu 6:
Hướng dẫn giải
Đáp án đúng là: C
. Do đó A sai.
(vì M là trung điểm của BC nên ). Do đó B sai.
. Do đó C đúng.
. Do đó D sai.
Câu 7:
Hướng dẫn giải
Đáp án đúng là: C
Vì ABCD là hình bình hành nên AB = DC = 4, AD = BC = 5.
Xét tam giác BDC:
Áp dụng hệ quả của định lí cos, ta có:
cos C = .
Mà
⇒ cos B = – cosC =
Xét tam giác ABC:
Áp dụng định lí cos ta được:
AC2 = AB2 + AC2 – 2.AB.AC.cosB
= 42 + 52 – 2.4.5.
= 33
⇒ AC = ≈ 5,7.
Câu 8:
Hướng dẫn giải
Đáp án đúng là: A
Vì ABCD là hình bình hành nên AB // CD, AD // BC và AB = CD, AD = BC.
Do đó: , .
Khi đó ta có:
. Do đó A đúng.
. Do đó B sai.
. Do đó C sai.
. Do đó D sai.
Câu 9:
Hướng dẫn giải
Đáp án đúng là: B
Vì N ⊂ X nên X phải chứa phần tử của tập hợp N nên X có ít nhất ba phần tử là 3 ; 4 ; 5.
Mặt khác X ⊂ M và X có bốn phần tử nên ta có :
X = {1; 3; 4; 5} hoặc X = {2; 3; 4; 5}.
Vậy có hai tập hợp X thỏa mãn.
Câu 10:
Hướng dẫn giải
Đáp án đúng là: A
Xét tam giác ABC:
Áp dụng định lí sin, ta có:
.
Câu 11:
Hướng dẫn giải
Đáp án đúng là: B
Hàm số xác định khi .
Suy ra D = [– 2; +∞) \ {3}.
Do đó ℝ\D = ( –∞; – 2).
Câu 12:
Hướng dẫn giải
Đáp án đúng là: A
Câu A là câu cảm thán không xác định được tính đúng sai nên không phải mệnh đề.
Câu 13:
Hướng dẫn giải
Đáp án đúng là: C
+) Cặp số (0; 0):
Thay x = 0 và y = 0 vào từng bất phương trình trong hệ ta thấy đều thỏa mãn.
Do đó (0; 0) là nghiệm của hệ bất phương trình.
+) Cặp số (1; 1):
Thay x = 1 và y = 1 vào từng bất phương trình trong hệ ta thấy đều thỏa mãn.
Do đó (1; 1) là nghiệm của hệ bất phương trình.
+) Cặp số (– 1; 1):
Thay x = – 1 và y = 1 vào từng bất phương trình trong hệ ta thấy cặp số không thỏa mãn bất phương trình 2x – 3y > – 2.
Do đó (– 1; 1) là nghiệm của hệ bất phương trình.
+) Cặp số (– 1; – 1):
Thay x = – 1 và y = – 1 vào từng bất phương trình trong hệ ta thấy đều thỏa mãn.
Do đó (– 1; – 1) là nghiệm của hệ bất phương trình.
Câu 14:
Hướng dẫn giải
Đáp án đúng là: C
Gọi M là trung điểm của cạnh BC.
Xét tam giác ABC, có: AM =
Ta có:
⇒
Câu 15:
Hướng dẫn giải
Đáp án đúng là: B
Tập hợp A gồm các số tự nhiên chia hết cho 2 và chia hết cho 3 nên A là tập các số chia hết cho 6.
Tập hợp B là tập gồm các số tự nhiên chia hết cho 12.
Mà các số chia hết cho 12 thì cũng chia hết cho 6, nhưng chia hết cho 6 chưa chắc chia hết cho 12. Do đó B ⊂ A.
Câu 16:
Hướng dẫn giải
Đáp án đúng là: A
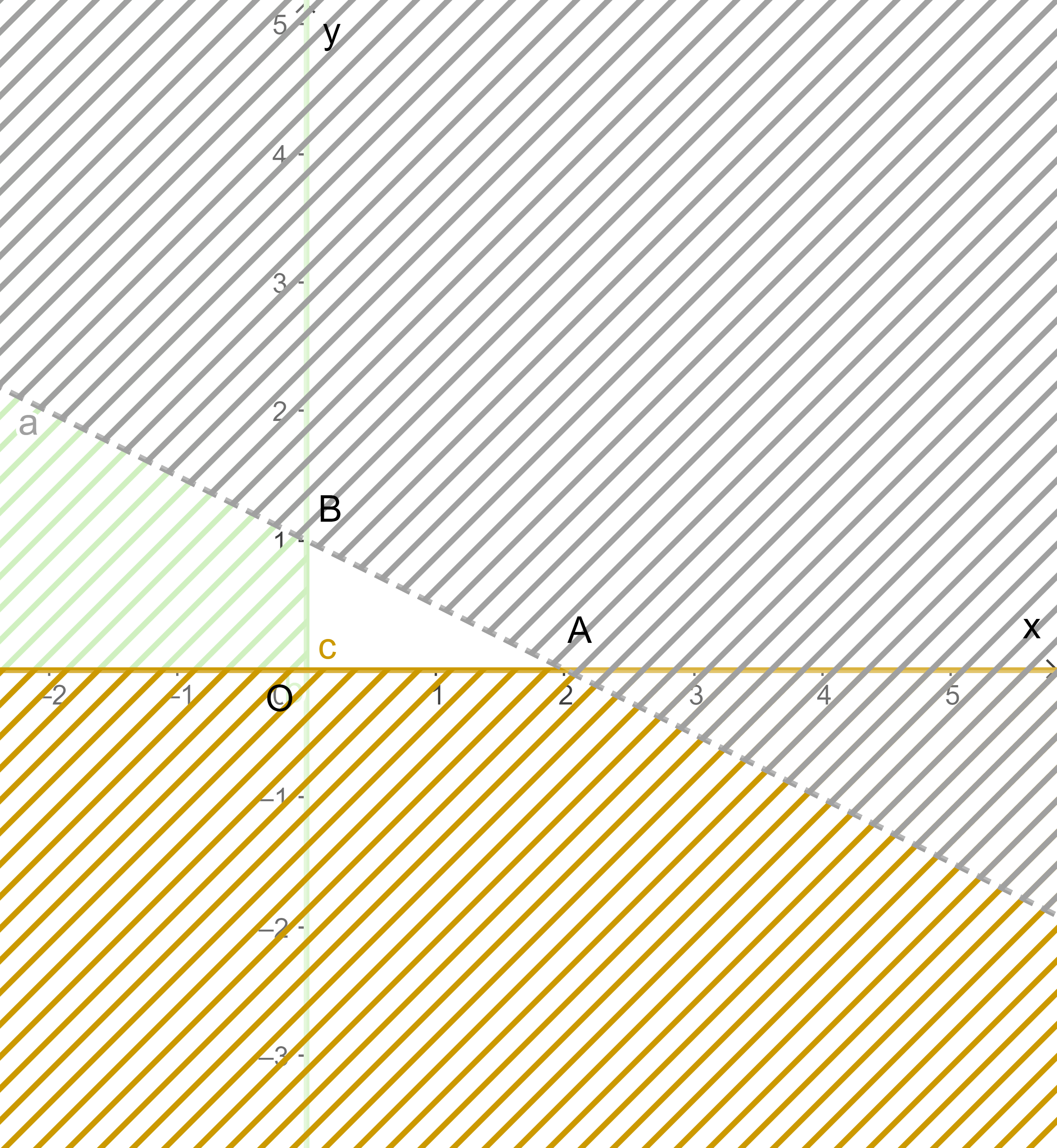
Miền nghiệm của hệ bất phương trình là miền trong tam giác OAB với A(2; 0), B(0; 1) và O (0; 0).
Câu 17:
Hướng dẫn giải
Đáp án đúng là: A
Với tam giác ABC các vectơ khác vectơ - không có điểm đầu và điểm cuối là ba đỉnh của tam giác là:
Vậy có tất cả 6 vectơ.
Câu 18:
Hướng dẫn giải
Đáp án đúng là: C
Xét phương trình: 2x2 – 5x – 7 = 0
⇔
⇒ .
Câu 19:
Hướng dẫn giải
Đáp án đúng là: C
Ta có:
. Do đó A sai.
. Do đó B sai.
. Do đó C đúng theo quy tắc 3 điểm.
. Do đó D sai.
Câu 20:
Hướng dẫn giải
Đáp án đúng là: D
Cạnh BC là cạnh lớn nhất nên góc đối diện A cũng là góc lớn nhất trong tam giác.
Xét tam giác ABC:
Áp dụng hệ quả của định lí cos ta có:
cosA =
⇒ > 90°.
Vậy tam giác ABC là tam giác tù với .
Câu 21:
Hướng dẫn giải
Đáp án đúng là: B
Mệnh đề phủ định của mệnh đề P là : “∀ x ∈ ℝ: 2x – 3 < 0”.
II. TỰ LUẬN( 3 ĐIỂM)
Bài 1. (1 điểm)
a) Cho các tập hợp A = {0; 1; 2; 3; 4; 5} và B = {2; 3; 4; 5; 6}. Tìm các tập hợp A ∪ B, A ∩ B.
b) Tìm m để A = (m – 1; 2] là tập con của tập B = (0; m + 9).
Lời giải
a) Ta có: A ∪ B = {0; 1; 2; 3; 4; 5; 6}.
A ∩ B = {2; 3; 4; 5}.
b) Để A là tập con của tập B thì .
Vậy với m > 1 thì tập A là tập con của tập B.
Bài 2.(1 điểm) Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức F(x; y) = 5x – 10y với cặp (x; y) thuộc vào miền nghiệm của hệ bất phương trình .
Lời giải
+) Biểu diễn miền nghiệm
Vẽ bốn đường thẳng:
d1: x = 1, d2: x = 4, d3: x + y = 5, d4: y = 0.
Biểu diễn từng miền nghiệm của mỗi bất phương trình trên mặt phẳng Oxy.
Miền không gạch chéo (hay chính là miền trong của tứ giác OABC với O(0; 0), A(5; 0), B(4; 1), C(5; 0) và bao gồm cả các cạnh trong hình vẽ là phần giao của các miền nghiệm và cũng là phần biểu diễn miền nghiệm của hệ bất phương trình đã cho.
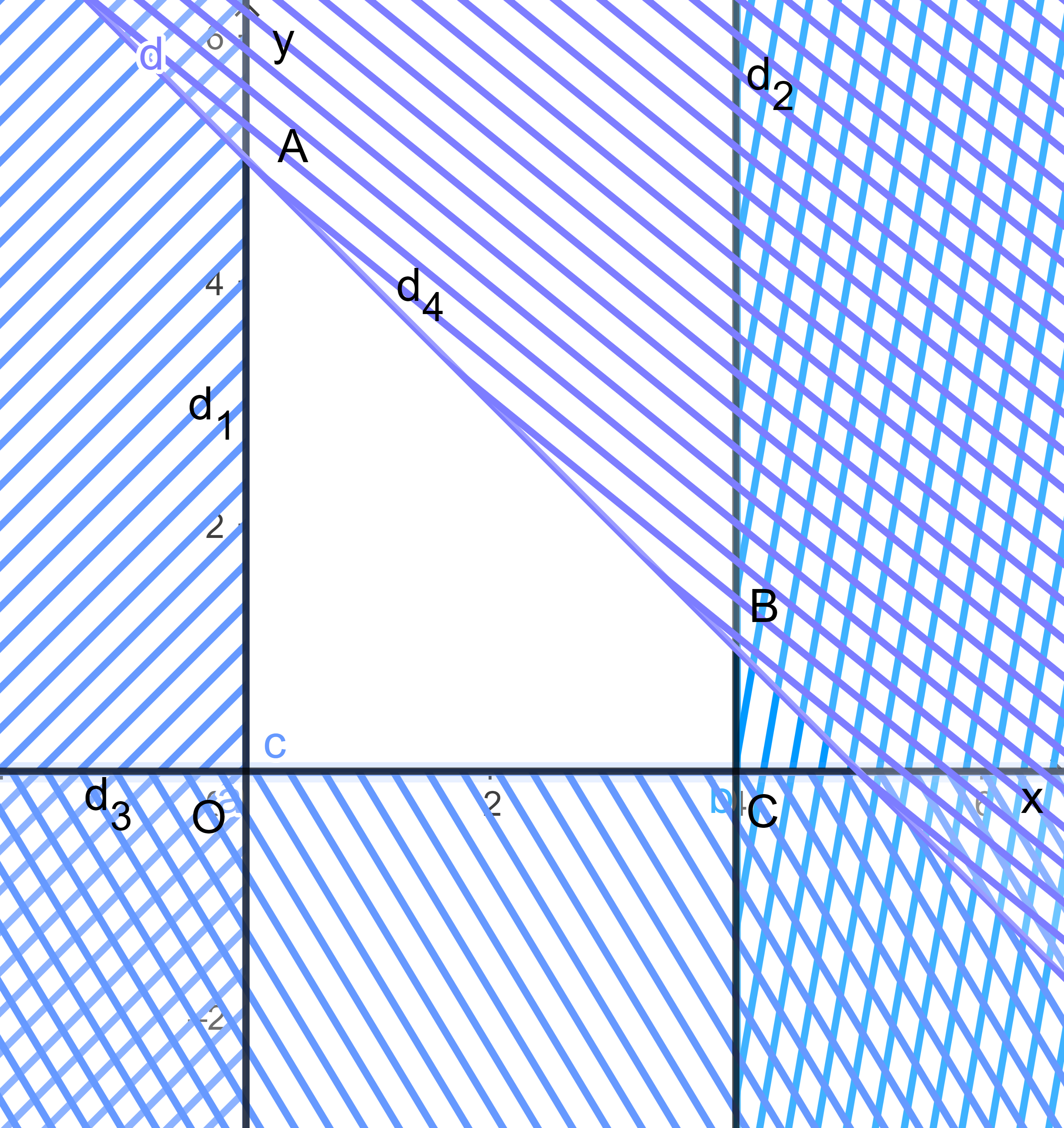
Ta chứng minh được giá trị lớn nhất và giá trị nhỏ nhất của biểu thức F đạt được trên các đỉnh của tứ giác OABC. Khi đó ta có:
Tại O(0; 0): F(0; 0) = 5.0 – 10.0 = 0;
Tại A(0; 5): F(0; 5) = 5.0 – 10.5 = – 50;
Tại B(4; 1): F(4; 1) = 5.4 – 10.1 = 10;
Tại C(5; 0): F(5; 0) = 5.5 – 10.0 = 25.
Vậy giá trị lớn nhất của F là 25 khi x = 5 và y = 0, giá trị nhỏ nhất của F là – 50 khi x = 0, y = 5.
Bài 3. (1 điểm)
a) (0,5 điểm) Cho tứ giác MNPQ. Gọi H, K lần lượt là trung điểm của MN và PQ. Chứng minh rằng .
b) (0,5 điểm) Cho hai điểm A, B. Tìm tập hợp điểm M thỏa mãn .
Lời giải
a) Ta có:
b) Ta có:
Xác định H, K sao cho: và
+ Ta được
M nằm trên đường trung trực HK hoặc trung trục AB.
Xem thêm các đề thi Giữa học kì 1 Toán học 10 hay, chi tiết khác:
Đề thi Giữa học kì 1 Toán 10 Kết nối tri thức (Có đáp án)...
Đề thi giữa kì 1 Toán 10 Cánh diều (Có đáp án)...
Xem thêm các đề thi Học kì 1 Toán học 10 hay, chi tiết khác:
Đề thi học kì 1 Toán 10 Kết nối tri thức (Có đáp án)...
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.