Toptailieu.vn biên soạn và giới thiệu Top 30 Đề thi Giữa học kì 2 Toán 10 (Chân trời sáng tạo 2024) có đáp án gồm các đề thi được tuyển chọn và tổng hợp từ các đề thi môn Toán THPT trên cả nước có hướng dẫn giải chi tiết giúp học sinh làm quen với các dạng đề, ôn luyện để đạt kết quả cao trong kì thi sắp tới. Mời các bạn đón xem:

Top 30 Đề thi Giữa học kì 2 Toán 10 (Chân trời sáng tạo 2024) có đáp án

Đề thi Học kì 2 Toán 10 Kết nối tri thức (Có đáp án) - Đề số 01

Phòng Giáo dục và Đào tạo ...

Đề thi Giữa học kì 2 Toán 10

Năm học 2022 - 2023

Môn: Toán học 10

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

Câu 1. Trong các véc tơ sau véc tơ nào không là pháp tuyến của đường thẳng có phương trình 3x−3y+4=0?

A. (1;1)       B. (3;−3)                              

C. (−2;2)         D. (6;−6)

Câu 2. Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có tọa độ các đỉnh là A(2;1), B(−1;2), C(3;−4). Phương trình nào sau đây là phương trình đường trung tuyến của tam giác ABC vẽ từ A?

A.  x−2y=0                     

B. x+2y−2=0                

C. 2x−y−1=0

D. 2x−y−3=0

Câu 3. Miền nghiệm của bất phương trình −x+2+2(y−2)<2(1−x) là nửa mặt phẳng không chứa điểm nào trong các điểm sau?

A. (1;1)   B. (4;2)                                

C. (0;0)     D. (1;−1)

Câu 4. Xét góc lượng giác (OM,OA)=α, trong đó M là điểm không thuộc các trục tọa độ Ox,Oy và thuộc góc phần tư thứ hai của hệ trục độ Oxy. Hãy chọn kết quả đúng trong các kết quả sau:

A. sinα<0,cosα>0                                                       

B. sinα>0,cosα>0                                           

C. sinα<0,cosα<0                                                       

D. sinα>0,cosα<0

Câu 5. Cho hai đường thẳng Δ1:a1x+b1y+c1=0 và Δ1:a2x+b2y+c2=0 trong đó a21+b21≠0,a22+b22≠0. Khẳng định nào sau đây sai?

A. Véc-tơ pháp tuyến của Δ1 và Δ2 không cùng phương với nhau thì Δ1 và Δ2 cắt nhau                      

B. Tích vô hướng hai véc tơ pháp tuyến Δ1 và Δ2 bằng 0 thì Δ1 và Δ2 vuông góc                                              

C. Véc-tơ pháp tuyến của Δ1 và Δ2 cùng phương với nhau thì Δ1 song song với Δ2             

D. Δ1 và Δ2 trùng nhau khi véc tơ pháp tuyến của chúng cùng phương với nhau và M∈Δ1⇒M∈Δ2

Câu 6. Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn (C):x2+y2−4x−5=0. Mệnh đề nào sau đây sai?

A. (C) cắt trục Oy tại một điểm phân biệt                                      

B. (C) có tâm A(2;0)                                  

C. (C) có bán kính R=3                                        

D. (C) cắt trục Ox tại hai điểm phân biệt

Câu 7. Hệ bất phương trình {2−x>02x+1>x−2 có tập nghiệm là

A. S=(2;+∞)    B. S=(−3;+∞)                    C. S=(−∞;3)     D. S=(−3;2)

Câu 8. Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng Δ có phương trình tham số {x=−1+2ty=−4+t. Điểm nào sau đây thuộc đường thẳng Δ?

A. N(1;−3)      B. Q(3;1)                                   

C. M(−3;1)       D. P(1;3)

Câu 9. Gọi D=[a;b] là tập xác định của hàm số y=√(2−√5)x2+(15−7√5)x+25−10√5. Khi đó M=a+b2 bằng

A. −5         B. 5         C. 1        D. 0

Câu 10. Trong các khẳng định sau, khẳng định nào là đúng?

A. {a<bc>0⇒ac<bc                                                

B. c<a<b⇒ac<bc                                                

C. a<b⇒ac<bc                                                                  

D. a<b⇒ac>bc

Câu 11. Trên đường tròn lượng giác với điểm gốc là A. Điểm M thuộc đường tròn sao cho cung lượng giác  có số đo 750. Gọi N là điểm đối xứng với điểm M qua gốc tọa độ O, mọi cung lượng giác có điểm đầu A và điểm cuối N có số đo bằng

A. −1050  

B. −1050+k3600,k∈Z

C. −1050 hoặc 2550 

D. 2550

Câu 12. Trong mặt phẳng với hệ trục tọa độ Oxy, cho các đường thẳng Δ1:2x−5y+15=0 và Δ2:{x=5−2ty=1+5t. Tính góc φ giữa Δ1 và Δ2.

A. φ=300       B. φ=900 

C. φ=600        D. φ=450

Câu 13. Trong mặt phẳng với hệ trục tọa độ Oxy, cho đường thẳng Δ:3x+4y+10=0 và điểm M(3;−1). Tính khoảng cách d từ điểm M đến đường thẳng Δ.

A. d=15√5  B. d=2  

C. d=3        D. d=135

Câu 14. Cho góc lượng giác α thỏa mãn 0<α<π2. Khẳng định nào sau đây là sai?

A. cos(α−π)<0 

B. tan(α+π)>0 

C. cos(α+π)>0 

D. sin(α+π)<0

Câu 15. Tập nghiệm S của hệ bất phương trình {x2−3x+2≤0x2−1≤0 là

A. S={1}     B. S={1;2} 

C. S=1        D. S=[−1;1]

Câu 16. Cặp bất phương trình nào sau đây là tương đương với nhau?

A. x−2≤0 và x2(x−2)≤0 

B. x−2≥0 và x2(x−2)≥0  

C. x−2<0 và x2(x−2)>0 

D. x−2<0 và x2(x−2)<0

Câu 17. Tập nghiệm của bất phương trình |x+1|−|x−2|≥3 là

A. S=[2;+∞)   B. S=(−2;1)                           

C. S=[−1;2]    D. (−∞;−1)

Câu 18. Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC với A(−1;−1), B(1;1), C(5;−3). Viết phương trình đường tròn ngoại tiếp ΔABC.

A. (x−2)2+(y+2)2=100

B. (x−2)2+(y−2)2=10 

C. (x−2)2+(y+2)2=10 

D. (x+2)2+(y+2)2=√10

Câu 19. Tập xác định của bất phương trình √x+1(x−2)2<x+1 là

A. D=(−1;+∞)∖{2} 

B. D=(−1;+∞) 

C. D=[−1;+∞) 

D. D=[−1;+∞)∖{2}

Câu 20. Tập nghiệm của bất phương trình (2x+8)(1−x)>0 có dạng (a;b). Khi đó b−a bằng

A. 6      B. 9      C. 5        D. 3

Câu 21. Cho góc α thỏa mãn sinα=1213 và π2<α<π. Tính cosα.

A. cosα=513     B. cosα=−113 

C. cosα=−513   D. cosα=113

Câu 22. Cho đường thẳng d1:5x−3y+5=0 và d2:3x+5y−2=0. Chọn phát biểu đúng trong các phát biểu sau:

A. d1 song song d2

B. d1 vuông góc d2 

C. d1 không vuông góc với d2 

D. d1 trùng d2

Câu 23. Bất phương trình mx>3 vô nghiệm khi

A. m<0      B. m>0

C. m=0      D. m≠0

Câu 24. Số nghiệm nguyên của bất phương trình x2−x−12≤0 là

A. 8    B. 9    C. 10     D. 11

Câu 25. Trong mặt phẳng với hệ trục tọa độ Oxy, phương trình nào sau đây không phải là phương trình của một đường tròn?

A. x2+y2−2x−2y+2=0

B. x2+y2−6y+4=0 

C. 2x2+2y2−8=0

D. 2x2+2y2−8x−2y+2=0

Câu 26. Bất phương trình 32−x<1 có tập nghiệm là

A. S=(−∞;−1]∪[2;+∞) 

B. S=(−1;2)

C. S=(−∞;−1)∪(2;+∞)            

D. S=[−1;2)

Câu 27. Tổng bình phương các nghiệm nguyên của bất phương trình |2x−3|≤1 bằng

A. 3     B. 5     C. 4      D. 6

Câu 28. Trong mặt phẳng với hệ trục tọa độ Oxy, viết phương trình tham số của đường thẳng d đi qua A(3;−2) có hệ số góc k=−2.

A. {x=3−2ty=−2+t 

B. {x=3+ty=−2−2t 

C. {x=3+2ty=−2+t 

D. {x=3+ty=−2+2t

Câu 29. Cho tam thức bậc hai f(x)=x2−bx+3. Với giá trị nào của b thì f(x)=0 có nghiệm?

A. b∈(−∞;−2√3]∪[2√3;+∞) 

B. b∈[−2√3;2√3]

C. b∈(−∞;−2√3)∪(2√3;+∞) 

D. b∈(−2√3;2√3)

Câu 30. Trên đường tròn lượng giác với điểm gốc A, cung lượng giác nào có các điểm biểu diễn tạo thành tam giác đều?

A. kπ2,k∈Z 

B. kπ,k∈Z 

C. kπ3,k∈Z

D. k2π3,k∈Z

Câu 31. Cho biết tanα=2. Tính giá trị P=cos2α−sin2α được:

A. P=35       

B. P=−45 

C. P=−35        

D. P=45

Câu 32. Số giá trị nguyên của m nhỏ hơn 2019 để hệ bất phương trình {x2+3x≥(x+1)2x−m<0 có nghiệm là

A. 2019        

B. 2017

C. 2018         

D. 2016

Câu 33. Cho f(x)=ax2+bx+c(a≠0). Điều kiện để f(x)>0 đúng ∀x∈R là

A. {a<0Δ>0     

B. {a>0Δ≤0

C. {a>0Δ<0      

D. {a>0Δ≥0

Câu 34. Trong mặt phẳng hệ trục tọa độ Oxy, cho các đường thẳng song song Δ1:3x+2y−3=0 và Δ2:3x+2y+2=0. Tính khoảng cách d giữa hai đường thẳng đó.

A. 1        B. 5

C. d=1√13       

D. d=5√1313

Câu 35. Bất phương trình √x+√4−x+2√4x−x2≥2 có tập nghiệm S=[a;b],a<b.

Tính P=a2019+b2019.

A. 1      

B. 24038     

C. 22019      

D. 44038

Câu 36. Bất phương trình √x−1>√x−2+√x−3 có bao nhiêu nghiệm nguyên dương?

A. 2    

B. 1      

C. 3       

D. 0

Câu 37. Đơn giản biểu thức P=cos(α−π2)+sin(α−π),α∈R ta được

A. P=sinα−cosα   

B. P=2sinα

C. P=cosα+sinα 

D. P=0

Câu 38. Tích của nghiệm nguyên âm lớn nhất và nghiệm nguyên dương nhỏ nhất của bất phương trình (3x−6)(x−2)(x+2)(x−1)>0 là

A. 8        

B. −6         

C. −4        

D. −9

Câu 39. Giá trị lớn nhất M của biểu thức F(x;y)=x+2y trên miền xác định bởi hệ {0≤y≤4x≥0x−y−1≤0x+2y−10≤0 là

A. M=10       

B. M=6

C. M=12       

D. M=8

Câu 40. Trong mặt phẳng với hệ trục tọa độ Oxy, cho hai đường thẳng d1:3x−y−1=0 và d2:x+y−2=0. Đường tròn có tâm I(−a;b),a>0 thuộc đường thẳng d1 tiếp xúc với đường thẳng d2 và đi qua A(2;−1). Khi đó, a thuộc khoảng

A. (−5;−4)    

B. (4;5) 

C. (3;4)       

D. (2;3)

Câu 41. Tính giá trị biểu thức P=(cot440+tan2260)cos4060cos3160−cot720cot180.

A. P=1        

B. P=12   

C. P=−12         

D. P=−1

Câu 42. Giải bất phương trình 2x(x−1)+1>√x2−x+1 được tập nghiệm S=(−∞;a)∪(b;+∞)(a<b). Tích P=ab bằng

A. 0          

B. 2       

C. 1      

D. −1

Câu 43. Cho đường thẳng (C):(x+1)2+(y−2)2=4 và đường thẳng d:3x−y+2=0. Viết phương trình đường thẳng d′ song song với đường thẳng d và chắn trên (C) một dây cung có độ dài lớn nhất.

A. 3x−y+5=0  

B. 3x−y+20=0   

C. 3x−y+13=0

D. 3x−y−5=0

Câu 44. Trong mặt phẳng với hệ trục tọa độ Oxy, đường thẳng đi qua A(0;1) tạo với đường thẳng d:3x−2y−5=0 một góc bằng 450 có hệ số góc k là

A. k=−15

B. [k=−5k=15  

C. [k=5k=−15

D. k=5

Câu 45. Giá trị lớn nhất của biểu thức P=sin6α+cos6α+msin2α, |m|<32 bằng

A. 1+3m29       

B. 1−3m4 

C.m2+33       

D. 1+3m4

Câu 46. Cho hai số thực dương x,y thỏa mãn x+y=1. Giá trị nhỏ nhất của S=1x+4y là

A. 5       

B. 9      

C. 4       

D. 2

Câu 47. Số nghiệm nguyên của bất phương trình x4−1>x2+2x thỏa mãn điều kiện |x|≤2019 là

A. 2019       

B. 4038  

C. 4037        

D. 4036

Câu 48. Trong mặt phẳng với hệ tọa độ Oxy, cho hình vuông ABCD. Gọi M,N lần lượt là trung điểm của các cạnh AB và CD. Biết rằng M(−12;2) và đường thẳng BN có phương trình 2x+9y−34=0. Khi đó, tọa độ B(a;b),(a<0). Tính a2+b2.

A. 25       

B. 13     

C. 17      

D. 5

Câu 49. Tìm tất cả các giá trị của tham số m để bất phương trình mx+4>0 nghiệm đúng với mọi x thỏa mãn |x|<8.

A. m∈[−12;0)∪(0;12]

B. m∈(−∞;12]

C. m∈[12;+∞)

D. m∈[−12;12]

Câu 50. Cho hai số thực x,y thỏa mãn x2+y2=x+y+xy. Đặt S=x+y. Khẳng định nào sau đây là đúng?

A. S>0     

B. S<0   

C. S2>16    

D. 0≤S≤4

Lời giải chi tiết

1. A	2. D	3. B	4. D	5. C
6.A	7.D	8.A	9.D	10.A
11.B	12.B	13.C	14.C	15.A
16.A	17.A	18.C	19.D	20.C
21.C	22.B	23.C	24.A	25.A
26.C	27.B	28.B	29.A	30.D
31.C	32.B	33.C	34.D	35.B
36.B	37.D	38.D	39.A	40.B
41.A	42.A	43.A	44.B	45.C
46.B	47.C	48.C	49.D	50.D

 

Câu 1 (NB) - Phương trình đường thẳng

Phương pháp:

Nếu đường thẳng Δ:ax+by+c=0 thì →n=(a;b) là VTPT của Δ.

Cách giải:

3x−3y+4=0⇒VTPT→n=(3;−3)=(1;−1)=k(1;−1)(k≠0,k∈Z)

+) Với k=3⇒VTPT→n=(3;−3)⇒ Đáp án B đúng.

+) Với k=−2⇒VTPT→n=(−2;2)⇒ Đáp án C đúng.

+) Với k=6⇒VTPT→n=(6;−6)⇒ Đáp án D đúng.  

Chọn A.

Câu 2 (TH) - Phương trình đường thẳng

Phương pháp:

Xác định tọa độ trung điểm của BC sau đó viết phương trình đường thẳng đi qua hai điểm A và M.

Cách giải:

Gọi M(xM;yM) là trung điểm của BC.

⇒{xM=xC+xB2yM=yC+yB2⇔{xM=−1+32yM=2+(−4)2⇔{xM=1yM=−1⇒M(1;−1)

Ta có: A(2;1), M(1;−1)

⇒→AM=(−1;−2)⇒→nAM=(2;−1)

Phương trình đường trung tuyến của tam giác ABC vẽ từ A đi qua A(2;1) nhận →nAM=(2;−1) là VTPT là :

2.(x−2)−1.(y−1)=0⇔2x−y−3=0

Chọn D.

Câu 3 (NB) - Bất phương trình

Phương pháp:

Thay tọa độ từng điểm vào bất phương trình và kiểm tra xem điểm đó có thỏa mãn bất phương trình hay không?

Cách giải:

+) (x;y)=(1;1) bất phương trình trở thành:

−1+2+2(1−2)<2(1−1)⇔−1<0 (thỏa mãn)

⇒ Miền nghiệm của bất phương trình −x+2+2(y−2)<2(1−x) là nửa mặt phẳng chứa điểm (1;1).

+) (x;y)=(4;2) bất phương trình trở thành:

−4+2+2(2−2)<2(1−4)⇔−2<−6 (vô lý)

⇒ Miền nghiệm của bất phương trình −x+2+2(y−2)<2(1−x) là nửa mặt phẳng không chứa điểm (4;2).

+) (x;y)=(0;0) bất phương trình trở thành:

−0+2+2(0−2)<2(1−x).0⇔−2<0(thỏa mãn)

⇒ Miền nghiệm của bất phương trình −x+2+2(y−2)<2(1−x) là nửa mặt phẳng chứa điểm (0;0).

+) (x;y)=(1;−1) bất phương trình trở thành:

−1+2+2(−1−2)<2(1−1)⇔−5<0 (thỏa mãn)

⇒ Miền nghiệm của bất phương trình −x+2+2(y−2)<2(1−x) là nửa mặt phẳng chứa điểm (1;−1).

Chọn B.

Câu 4 (NB) - Giá trị lượng giác của một góc bất kỳ từ 0 đến 180 độ

Phương pháp:

Sử dụng bảng xác định dấu của các giá trị lượng giác.

Cách giải:

Vì M là điểm không thuộc các trục tọa độ Ox,Oy và thuộc góc phần tư thứ hai của hệ trục độ Oxy nên sinα>0,cosα<0.

Chọn D.

Câu 5 (TH) - Phương trình đường thẳng

Phương pháp:

Xác định VTPT của Δ1,Δ2. Sử dụng điều kiện hai véc-tơ cùng phương, đường thẳng song song, trùng nhau, vuông góc.

Cách giải:

Δ1:a1x+b1y+c1=0⇒→n1=(a1;b1)

Δ2:a2x+b2y+c2=0⇒→n2=(a2;b2)

*) →n1 và →n2 không cùng phương ⇒Δ1 và Δ2 cắt nhau ⇒ Đáp án A đúng.

*) →n1.→n2=0⇒Δ1 và Δ2 vuông góc⇒ Đáp án B đúng.

*) →n1 và →n2 cùng phương thì →n1=k→n2(k≠0)

+ Nếu k=1 thì →n1=→n2⇒Δ1 và Δ2 trùng nhau.

+ Nếu k≠1 thì →n1=k→n2⇒Δ1 và Δ2 song song.

⇒ Đáp án C sai (vì hai véc tơ cùng phương thì chúng có thể song song với nhau hoặc trùng nhau)

*) →n1 và →n2 cùng phương thì Δ1 và Δ2 trùng nhau hoặc song song với nhau. Kết hợp với điều kiện M∈Δ1⇒M∈Δ2 suy ra Δ1 và Δ2 trùng nhau. ⇒ Đáp án D đúng

Chọn C.

Câu 6 (TH) - Phương trình đường tròn

Phương pháp:

Xác định tâm và bán kính của đường tròn; Xác định giao điểm của đường tròn với Ox,Oy.

Cách giải:

Ta có: x2+y2−4x−5=0⇔(x2−4x+4)+y2=9⇔(x−2)2+y2=9

⇒(C) được viết dưới dạng: (x−2)2+y2=9

⇒(C) có tâm A(2;0) và bán kính R=3.

⇒ Đáp án B và C đúng.

*) Nếu x=0, (C) trở thành:

(0−2)2+y2=9⇔y2=5⇔[y=−√5y=√5

⇒(C) cắt Oy tại hai điểm phân biệt (0;−√5) và (0;√5)

⇒ Đáp án A sai.

*) Nếu y=0, (C) trở thành:

(x−2)2=9⇔[x−2=3x−2=−3⇔[x=5x=−1

⇒(C) cắt Ox tại hai điểm phân biệt (5;0) và (−1;0)

⇒ Đáp án D đúng.

Chọn A.

Câu 7 (TH) - Bất phương trình và hệ bất phương trình một ẩn

Phương pháp:

Giải hai bất phương trình rồi kết hợp tập nghiệm.

Cách giải:

{2−x>02x+1>x−2⇔{2−x>0x+3>0⇔{x<2x>−3⇔−3<x<2

⇒ Hệ bất phương trình {2−x>02x+1>x−2 có tập nghiệm là S=(−3;2).

Chọn D.

Câu 8 (TH) - Phương trình đường thẳng

Phương pháp:

Thay từng điểm vào phương trình tham số của đường thẳng Δ và xét xem diểm đó có thỏa mãn hay không.

Cách giải:

+) Thay x=1;y=−3 vào đường thẳng {x=−1+2ty=−4+t ta được:

{1=−1+2t−3=−4+t ⇔{t=1t=1(thỏa mãn)

⇒ Điểm N(1;−3) thuộc đường thẳng Δ:{x=−1+2ty=−4+t

+) Thay x=3;y=1 vào đường thẳng {x=−1+2ty=−4+t ta được:

{3=−1+2t1=−4+t⇔{t=2t=5 (không thỏa mãn)

⇒ Điểm Q(3;1) không thuộc đường thẳng Δ:{x=−1+2ty=−4+t

+) Thay x=−3;y=1 vào đường thẳng {x=−1+2ty=−4+t ta được:

{−3=−1+2t1=−4+t⇔{t=−1t=5 (không thỏa mãn)

⇒ Điểm M(−3;1) không thuộc đường thẳng Δ:{x=−1+2ty=−4+t

+) Thay x=1;y=3 vào đường thẳng {x=−1+2ty=−4+t ta được:

{1=−1+2t3=−4+t ⇔{t=1t=7(không thỏa mãn)

⇒ Điểm P(1;3) không thuộc đường thẳng Δ:{x=−1+2ty=−4+t

Chọn A.

Câu 9 (TH) - Hàm số

Phương pháp:

Hàm số y=√f(x) xác định khi và chỉ khi f(x)≥0. Từ đó, tìm a, b và tính giá trị của biểu thức M=a+b2

Cách giải:

Hàm số y=√(2−√5)x2+(15−7√5)x+25−10√5 xác định khi và chỉ khi

(2−√5)x2+(15−7√5)x+25−10√5≥0⇔x2+(5−√5)x−5√5≤0⇔(x+5)(x−√5)≤0⇔−5≤x≤√5

⇒ Tập xác định của hàm số y=√(2−√5)x2+(15−7√5)x+25−10√5 là D=[−5;√5].

⇒a=−5;b=√5

⇒M=a+b2=(−5)+(√5)2=0

Chọn D.

Câu 10 (TH) - Bất đẳng thức

Phương pháp:

Sử dụng các tính chất cơ bản của bất đẳng thức.

Cách giải:

+) Xét đáp án A

{a<bc>0⇒{a−b<0c>0⇒(a−b)c<0⇒ac−bc<0⇒ac<bc

⇒ Đáp án A đúng.

+) Xét đáp án B

c<a<b

Giả sử c<0⇒ac>bc (trái với đề bài)

⇒ Đáp án B sai.

+) Xét đáp án C

a<b

Giả sử c<0⇒ac>bc (trái với đề bài)

⇒ Đáp án C sai.

+) Xét đáp án D

a<b

Giả sử c>0⇒ac<bc (trái với đề bài)

⇒ Đáp án D sai.

Chọn A.

Câu 11 (TH) - Cung và góc lượng giác

Phương pháp:

Xác định vị trí các điểm M,N và xác định góc hình học ∠AOM,∠MON. Từ đó, xác định số đo của cung lượng giác AN.

Cách giải:

 

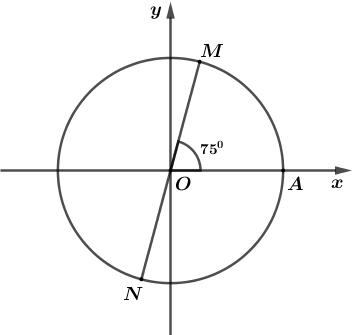
Ta có: ∠AOM=750,∠MON=1800

⇒ Cung lượng giác có điểm đầu A và điểm cuối N có số đo bằng −1050+k3600,k∈Z.

Chọn B.

Câu 12 (TH) - Phương trình đường thẳng

Phương pháp:

Gọi →n1,→n2 lần lượt là VTPT của Δ1 và Δ2.

⇒cos(Δ1,Δ2)=|cos(→n1,→n2)|=|→n1.→n2||→n1|.|→n2|

Cách giải:

Δ1:2x−5y+15=0⇒→nΔ1=(2;−5)

Δ2:{x=5−2ty=1+5t⇒→uΔ2=(−2;5)⇒→nΔ2=(5;2)

cos(Δ1,Δ2)=cosφ=|cos(→nΔ1,→nΔ1)|=|2.5+(−5).2|√22+(−5)2.√52+22=0

⇒cosφ=0⇒φ=900.

Chọn B.

Câu 13 (TH) - Phương trình đường thẳng

Phương pháp:

Khoảng cách từ điểm M0(x0,y0) đến đường thẳng Δ:ax+by+c=0 được tính bằng công thức:

d(M0,Δ)=|ax0+by0+c|√a2+b2

Cách giải:

d(M,Δ)=|3.3+4.(−1)+10|√32+42=155=3

Chọn C.

Câu 14 (TH) - Giá trị lượng giác của một góc bất kỳ từ 0 đến 180 độ

Phương pháp:

Biến đổi 0<α<π2⇒−π<α−π<−π2. Sau đó sử dụng bảng xác định dấu của các giá trị lượng giác.

Cách giải:

Ta có :

0<α<π2⇒−π<α−π<−π2⇒cos(α−π)<0

⇒ Đáp án A đúng.

0<α+π<π2⇒π<α+π<3π2⇒{cos(α+π)<0sin(α+π)<0⇒{tan(α+π)>0cot(α+π)>0

⇒ Đáp án B và D đúng ; Đáp án C sai.

Chọn C.

Câu 15 (TH): - Bất phương trình và hệ bất phương trình một ẩn

Phương pháp:

Giải từng bất phương trình sau đó kết hợp tập nghiệm của hai bất phương trình đó.

Cách giải:

{x2−3x+2≤0x2−1≤0⇔{(x−1)(x−2)≤0(x−1)(x+1)≤0⇔{1≤x≤2−1≤x≤1⇔x=1

Vậy tập nghiệm của hệ bất phương trình là S={1}.

Chọn A.

Câu 16 (TH) - Bất phương trình

Phương pháp:

Hai bất phương trình được gọi là tương đương nếu nó có cùng tập nghiệm.

Cách giải:

*) Xét đáp án A

+) x−2≤0⇔x≤2

+) x2(x−2)≤0⇔{x2≥0x−2≤0⇔{∀x∈Rx≤2⇔x≤2

Vậy cặp bất phương trình x−2≤0 và x2(x−2)≤0 tương đương.

*) Xét đáp án B

+) x−2≥0⇔x≥2

+) x2(x−2)≥0⇔{x2≥0x−2≥0⇔[x=0x≥2

Vậy cặp bất phương trình x−2≥0 và x2(x−2)≥0 không tương đương.

*) Xét đáp án C

+) x−2<0⇔x<2

+) x2(x−2)>0⇔{x2>0x−2>0⇔{x≠0x>2⇔x>2

Vậy cặp bất phương trình x−2<0 và x2(x−2)>0 không tương đương.

*) Xét đáp án D

+) x−2<0⇔x<2

+) x2(x−2)<0⇔{x2>0x−2<0⇔{x2>0x<2⇔{x≠0x<2

Vậy cặp bất phương trình x−2<0 và x2(x−2)<0 không tương đương.

Chọn A.

Câu 17 (TH) - Bất phương trình

Phương pháp:

Biến đổi bất phương trình |x+1|−|x−2|≥3 về dạng |x+1|≥3+|x−2|. Sau đó, bình phương hai vế để giải bất phương trình.

Cách giải:

|x+1|−|x−2|≥3⇔|x+1|≥|x−2|+3⇔(x+1)2≥(|x−2|+3)2⇔(x+1)2≥(x−2)2+6|x−2|+9⇔x2+2x+1≥x2−4x+4+6|x−2|+9⇔2x+1+4x−4−9≥6|x−2|⇔6x−12≥6|x−2|⇔6(x−2)≥6|x−2|⇔x−2≥|x−2|⇔x−2≥0⇔x≥2

⇒x∈[2;+∞)

Vậy  tập nghiệm của bất phương trình |x+1|−|x−2|≥3 là S=[2;+∞).

Chọn A.

Câu 18 (TH) - Phương trình đường tròn

Phương pháp:

I là tâm của đường tròn ngoại tiếp ΔABC khi và chỉ khi AI=BI=CI.

Cách giải:

Gọi I(a;b) là tâm của đường tròn ngoại tiếp ΔABC.

Khi đó, ta có:

{AI=BIBI=CI⇔{(a+1)2+(b+1)2=(a−1)2+(b−1)2(a−1)2+(b−1)2=(a−5)2+(b+3)2⇔{4a+4b=08a−8b=32⇔{a=2b=−2

⇒I(2;−2), R=AI=√(2+1)2+(−2+1)2=√10

Phương trình đường tròn ngoại tiếp ΔABC có tâm I(2;−2) và R=√10 là: (x−2)2+(y+2)2=10

Chọn C.

Câu 19 (TH): - Bất phương trình

Phương pháp:

√f(x)g(x) xác định khi và chỉ khi {f(x)g(x)≥0g(x)≠0

Cách giải:

Bất phương trình √x+1(x−2)2<x+1 xác định khi và chỉ khi :

 {x−2≠0x+1(x−2)2≥0⇔{x≠2x+1≥0⇔{x≠2x≥−1

Vậy D=[−1;+∞)∖{2}.

Chọn D.

Câu 20 (TH) - Bất phương trình

Phương pháp:

Giải bất phương trình, từ đó tìm a và b để tính giá trị biểu thức b−a.

Cách giải:

Bất phương trình: (2x+8)(1−x)>0

Ta có bảng xét dấu:

 

Dựa vào bảng xét dấu, tập nghiệm của bất phương trình (2x+8)(1−x)>0 là S=(−4;1).

⇒a=−4;b=1

⇒b−a=1−(−4)=5

Chọn C.

Câu 21 (TH): - Giá trị lượng giác của một góc bất kỳ từ 0 đến 180 độ

Phương pháp:

Sử dụng công thức sin2α+cos2α=1 để tìm cosα (chú ý bảng xét dấu các giá trị lượng giác).

Cách giải:

Áp dụng công thức: sin2α+cos2α=1

⇒cos2α=1−sin2α=1−(1213)2=25169

⇒[cosα=513cosα=−513

Mà π2<α<π nên cosα<0, do đó cosα=−513.

Chọn C.

Câu 22 (TH): - Phương trình đường thẳng

Phương pháp:

Sử dụng vị trí tương đối của hai đường thẳng:

+ Nếu a1a2≠b1b2 thì hai đường thẳng cắt nhau.

+ Nếu a1a2=b1b2≠c1c2 thì hai đường thẳng song song.

+ Nếu a1a2=b1b2=c1c2 thì hai đường thẳng trùng nhau.

+ Nếu a1a2+b1b2=0 thì hai đường thẳng vuông góc

Cách giải:

d1:5x−3y+5=0⇒→n1=(5;−3)

d2:3x+5y−2=0x⇒→n2=(3;5)

⇒→n1.→n2=5.3+(−3).5=0

⇒d1 vuông góc d2.

Chọn B.

Câu 23 (TH) - Bất phương trình

Phương pháp:

Sử dụng phương pháp giải và biện luận bất phương trình.

Cách giải:

+) m=0, bất phương trình trở thành: 0x>3⇔0>3 (vô lý)

⇒ Bất phương trình vô nghiệm khi m=0.

+) m≠0, ta có: mx>3⇔x>3m

⇒ Tập nghiệm của BPT là S=(3m;+∞).

Kết luận:

+ Với m=0: Bất phương trình vô nghiệm

+ Với m≠0: Bất phương trình có tập nghiệm là S=(3m;+∞).

Chọn C.

Câu 24 (TH) - Bất phương trình

Phương pháp:

Giải bất phương trình và xác định các giá trị nguyên thuộc tập nghiệm của bất phương trình.

Cách giải:

x2−x−12=0⇔[x=−3x=4

Ta có bảng xét dấu:

⇒ Tập nghiệm của bất phương trình x2−x−12≤0 là S=[−3;4].

Mà x∈Z⇒x∈{−3;−2;−1;0;1;2;3;4}.

Vậy bất phương trình có 8 nghiệm nguyên.

Chọn A.

Câu 25 (TH) - Phương trình đường tròn

Phương pháp:

Phương trình đường tròn x2+y2−2ax−2by+c=0 với các số a,b,c thỏa mãn điều kiện a2+b2>c.

Cách giải:

+) Xét đáp án A: x2+y2−2x−2y+2=0

Ta có: a=1,b=1,c=2⇒a2+b2=c(ktm)

⇒x2+y2−2x−2y+2=0 không phải là phương trình của một đường tròn.

+) Xét đáp án B: x2+y2−6y+4=0

Ta có: a=0,b=3,c=0⇒a2+b2>c(tm)

⇒x2+y2−6y+4=0 là phương trình đường tròn có tâm I(0;3),R=√5.

+) Xét đáp án C: 2x2+2y2−8=0

Ta có: a=0,b=0,c=−8⇒a2+b2>c(tm)

⇒2x2+2y2−8=0 là phương trình đường tròn có tâm I(0;0),R=2.

+) Xét đáp án D: 2x2+2y2−8x−2y+2=0

Ta có: a=4,b=1,c=2⇒a2+b2>c(tm)

⇒2x2+2y2−8x−2y+2=0 là phương trình đường tròn có tâm I(2;12),R=√132.

Chọn A.

Câu 26 (TH) - Bất phương trình

Phương pháp:

Tìm ĐKXĐ, quy đồng và giải bất phương trình.

Cách giải:

ĐKXĐ: x≠2

32−x<1⇔32−x−1<0⇔3−2+x2−x<0⇔1+x2−x<0⇔[{1+x>02−x<0{1+x<02−x>0⇔[{x>−1x>2{x<−1x<2⇔[x>2x<−1

Kết hợp với ĐKXĐ ⇒x∈(−∞;−1)∪(2;+∞)

Vậy tập nghiệm của bất phương trình là S=(−∞;−1)∪(2;+∞).

Chọn C.

Câu 27 (TH) - Bất phương trình

Phương pháp:

Với a>0, |f(x)|≤a⇔−a≤f(x)≤a và giải bất phương trình, xác định nghiệm nguyên thuộc tập nghiệm.

Cách giải:

|2x−3|≤1⇔−1≤2x−3≤1⇔2≤2x≤4⇔1≤x≤2

Mà x∈Z⇒x∈{1;2}.

Tổng bình phương các nghiệm của bất phương trình là: 12+22=5

Chọn B.

Câu 28 (TH) - Phương trình đường thẳng

Phương pháp:

Gọi phương trình đường thẳng d có dạng: y=ax+b (với a là hệ số góc). Từ yêu cầu của đề bài để tìm  a,b.

Cách giải:

Gọi phương trình đường thẳng d có dạng: y=ax+b

+) d có hệ số góc k=−2 nên a=−2 (1)  

+) d đi qua A(3;−2) nên ta có: −2=3a+b (2)

Thay (1)vào (2)ta được: −2=3.(−2)+b⇔b=4

⇒ PTTQ của đường thẳng d có dạng :

 y=−2x+4⇔−2x−y+4=0

⇒→nd=(−2;−1)⇒→ud=(1;−2)

⇒ PTTS của đường thẳng d đi qua A(3;−2) nhận →ud=(1;−2) là VTCP có dạng là :  {x=3+ty=−2−2t

Chọn B.

Câu 29 (TH) - Phương trình bậc hai

Phương pháp:

f(x)=0 có nghiệm khi và chỉ khi Δ≥0

Cách giải:

 f(x)=0 có nghiệm ⇔x2−bx+3=0 có nghiệm ⇔Δ≥0⇔b2−12≥0⇔[b≥2√3b≤−2√3

⇒b∈(−∞;−2√3]∪[2√3;+∞)

Chọn A.

Câu 30 (VD): - Cung và góc lượng giác

Phương pháp:

Sử dụng tính chất tam giác đều, định nghĩa góc nội tiếp, góc ở tâm của đường tròn.

Cách giải:

Tam giác đều có góc ở đỉnh là 600 nên góc ở tâm là 1200 tương ứng k2π3(k∈Z).

Chọn D.

Câu 31 (TH) - Công thức lượng giác

Phương pháp:

Sử dụng công thức tanα=sinαcosα và sin2α+cos2α=1 để tìm sin2α, cos2α.

Cách giải:

Theo đề bài: tanα=2⇔sinαcosα=2⇔sin2αcos2α=4⇔sin2α=4cos2α

Ta lại có: sin2α+cos2α=1⇒5cos2α=1⇔cos2α=15⇒sin2α=1−15=45

P=cos2α−sin2α=15−45=−35

Vậy P=−35 khi tanα=2.

Chọn C.

Câu 32 (TH) - Bất phương trình và hệ bất phương trình một ẩn

Phương pháp:

Giải từng bất phương trình, từ đó tìm điều kiện của m để hệ bất phương trình có nghiệm.

Cách giải:

{x2+3x≥(x+1)2x−m<0⇔{x2+3x≥x2+2x+1x<m⇔{x≥1x<m

Bất phương trình có nghiệm khi và chỉ khi m>1.

Kết hợp với điều kiện m<2019,m∈Z suy ra {m∈Z1<m<2019⇒m∈{2;3;…;2018}.

Vậy có 2017 giá trị nguyên của m thỏa mãn điều kiện đề bài.

Chọn B.

Câu 33 (TH) - Dấu của tam thức bậc hai

Phương pháp:

Sử dụng các định lý về dấu của tam thức bậc hai.

Cách giải:

f(x)=ax2+bx+c>0 đúng ∀x∈R khi và chỉ khi {a>0Δ<0.

Chọn C.

Câu 34 (TH) - Phương trình đường thẳng

Phương pháp:

A∈Δ1⇒d(Δ1,Δ2)=d(A,Δ2)

Công thức tính khoảng cách từ điểm M(x0;y0) đến đường thẳng Δ:ax+by+c=0.

d(M,Δ)=|ax0+by0+c|√a2+b2

Cách giải:

Lấy A(1;0)∈Δ1:3x+2y−3=0.

d(Δ1,Δ2)=d(A,Δ2)=|3.1+2.0+2|√32+22=5√13=5√1313

Chọn D.

Câu 35 (TH) - Bất phương trình

Phương pháp:

Tìm ĐKXĐ và giải bất phương trình bằng cách đặt t=√x+√4−x(t≥0).

Cách giải:

ĐKXĐ: {x≥04−x≥0⇔{x≥0x≤4⇔0≤x≤4

Đặt t=√x+√4−x(t≥0)

⇒t2=x+2.√x.√4−x+4−x

⇔t2=2√x(4−x)+4=2√4x−x2+4

Bất phương trình trở thành:

t+t2−4≥2⇔t2+t−6≥0⇔[t≥2t≤−3

Kết hợp với điều kiện ta được t≥2.

⇒t2≥4⇔2√4x−x2+4≥4⇔2√4x−x2≥0⇔√4x−x2≥0⇔4x−x2≥0⇔0≤x≤4

⇒x∈[0;4]⇒a=0;b=4

Thay a=0,b=4 vào biểu thức P=a2019+b2019 ta được: P=02019+42019=(22)2019=24038

Chọn B.

Câu 36 (TH) - Bất phương trình

Phương pháp:

Tìm ĐKXĐ sau đó bình phương hai vế.

√A<B⇔{B>0A≥0A<B2

Cách giải:

ĐKXĐ: {x−1≥0x−2≥0x−3≥0⇔{x≥1x≥2x≥3⇔x≥3

√x−1>√x−2+√x−3⇔x−1>x−2+x−3+2√(x−2)(x−3)⇔2√(x−2)(x−3)<4−x⇔{4−x>0(x−2)(x−3)≥04(x−2)(x−3)<(4−x)2⇔{x<4[x≤2x≥34x2−20x+24<16−8x+x2⇔{x<4[x≤2x≥33x2−12x+8<0⇔{[x≤23≤x<46−2√33<x<6+2√33⇔x∈(6−2√33;2]∪[3;6−2√33)

Mà x∈Z+ và x≥3 nên x=3.

Chọn B.

Câu 37 (TH) - Công thức lượng giác

Phương pháp:

Sử dụng công thức lượng giác của các cung liên quan đặc biệt.

Cách giải:

Với α∈R ta có:

P=cos(α−π2)+sin(α−π)P=cos[−(π2−α)]+sin[−(π−α)]P=cos(π2−α)−sin(π−α)P=sinα−sinαP=0

Vậy P=0.

Chọn D.

Câu 38 (TH): - Bất phương trình

Phương pháp:

Lập bảng xét dấu để giải bất phương trình. Từ tập nghiệm của bất phương trình tìm giá trị nguyên âm lớn nhất, giá trị nguyên dương nhỏ nhất.

Cách giải:

(3x−6)(x−2)(x+2)(x−1)>0⇔(x−2)2(x+2)(x−1)>0

Ta có bảng xét dấu:

 

 

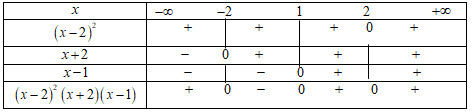
⇒x∈(−∞;−2)∪(1;2)∪(2;+∞)

Giá trị nguyên âm lớn nhất của x là −3.

Giá trị nguyên dương nhỏ nhất của x là 3.

⇒ Tích của chúng là 3.(−3)=−9.

Chọn D.

Câu 39 (TH) - Hệ trục tọa độ

Phương pháp:

+ Biểu diễn các đường thẳng trên cùng một mặt phẳng tọa độ

+ Xác định miền nghiệm của hệ bất phương trình

+ Xác định tọa độ các đỉnh của miền nghiệm đó, thay vào F(x;y)=x+2y và tìm giá trị lớn nhất.

Cách giải:

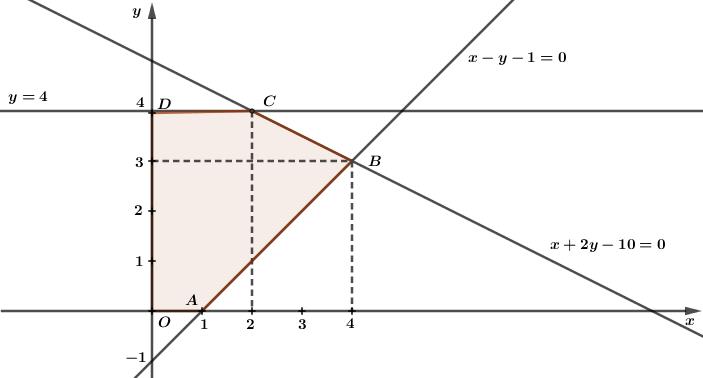
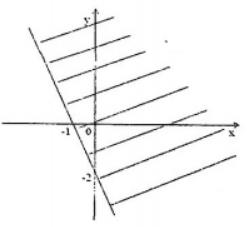
Quan sát đồ thị, ta thấy miền nghiệm của hệ bất phương trình là phần mặt phẳng (ngũ giác OABCD).

Khi đó, ta có các đỉnh O(0;0),A(1;0),B(4;3),C(2;4),D(0;4).

⇒{F(0;0)=0F(1;0)=1F(4;3)=10F(2;4)=10F(0;4)=8⇒M=10

Chọn A.

Câu 40 (TH) - Ôn tập chương 3: Phương pháp tọa độ trong mặt phẳng

Phương pháp:

I(−a;b)∈d1:3x−y−1=0⇒I(−a;−3a−1)

Kết hợp với điều kiện IA=d(I,d2) để tìm a.

Cách giải:

Vì I(−a;b),a>0 thuộc đường thẳng d1 nên I(−a;−3a−1).

Khoảng cách từ I(−a;3a−1) đến đường thẳng d2:x+y−2=0 là:

d(I,d2)=|−a−3a−1−2|√12+12=|−4a−3|√2

I(−a;−3a−1),A(2;−1)⇒IA=√(2+a)2+9a2

Vì đường tròn (I) đi qua A(2;−1) nên IA=d(I,d2).

⇒√(2+a)2+9a2=|−4a−3|√2⇔(2+a)2+9a2=16a2+24a+92⇔4+4a+a2+9a2=16a2+24a+92⇔8+8a+20a2=16a2+24a+9⇔4a2−16a−1=0⇔[a=4+√172(tm)a=4−√172(ktm)⇒a=4+√172∈(4;5)

Chọn B.

Câu 41 (VD) - Công thức lượng giác

Phương pháp:

Sử dụng công thức lượng giác của các cung liên quan đặc biệt.

Cách giải:

P=(cot440+tan2260)cos4060cos3160−cot720cot180P=−(tan460+tan460)sin3160cos3160−cot720tan720P=−(tan460+tan460)tan3160−1P=−2tan460tan1360−1P=2tan460tan440−1P=2tan460cot460−1P=2−1=1

Vậy P=1.

Chọn A.

Câu 42 (TH) - Bất phương trình

Phương pháp:

Tìm ĐKXĐ và đặt √x2−x+1=t(t≥0), sau đó giải bất phương trình tìm a và b.

Cách giải:

ĐKXĐ: x∈R

Đặt √x2−x+1=t(t≥0)

⇒x2−x=t2−1⇒x(x−1)=t2−1

Bất phương trình trở thành:

 2(t2−1)+1>t⇔2t2−t−1>0⇔[t<−12(ktm)t>1(tm)

⇒√x2−x+1>1⇔x2−x+1>1⇔x2−x>0⇔x(x−1)>0⇔[x>1x<0

⇒x∈(−∞;0)∪(1;+∞)

⇒ Tập nghiệm của bất phương trình là S=(−∞;0)∪(1;+∞).

⇒a=0,b=1

⇒P=a.b=0.1=0

Chọn A.

Câu 43 (TH) - Ôn tập chương 3: Phương pháp tọa độ trong mặt phẳng

Phương pháp:

Xác định tâm và bán kính của (C).

Giả sử d//d′:3x−y+c=0. Dây cung có độ dài lớn nhất là đường kính ⇒d(I,d′)=0. Từ đó tìm được c.

Cách giải:

(C):(x+1)2+(y−2)2=4⇒{T鈓I(−1;2)R=2

Giả sử đường thẳng d′ song song với d:3x−y+2=0 có dạng 3x−y+c=0

Vì dây cung có độ dài lớn nhất là đường kính nên d′ đi qua tâm I(−1;2).

⇒d(I,d′)=0⇒3.(−1)−2+c=0⇔c=5

Vậy d′:3x−y+5=0.

Chọn A.

Câu 44 (TH) - Phương trình đường thẳng

Phương pháp:

Gọi d′:y=kx+a là đường thẳng cần tìm.

Sử dụng công thức tính góc giữa hai đường thẳng: cos(d,d′)=|→nd.→nd′||→nd|.|→nd′|

Cách giải: 

Gọi d′:y=kx+a là đường thẳng cần tìm.

Vì d′ đi qua A(0;1) nên ta có: 1=k.0+a⇔a=1

Ta có:

d:3x−2y−5=0⇒→nd=(3;−2)

d′:kx−y+1=0⇒→nd′=(k;−1)

Theo đề bài, ta có:

cos(d,d′)=cos450=|→nd.→nd′||→nd|.|→nd′|=|3.k+(−2).(−1)|√32+(−2)2.√k2+1

⇔√22=|3.k+(−2).(−1)|√32+(−2)2.√k2+1⇔√22=|3k+2|√13(k2+1)⇔24=9k2+12k+413k2+13⇔26k2+26=36k2+48k+16⇔10k2+48k−10=0⇔(k+5)(5k−1)=0⇔[k+5=05k−1=0⇔[k=−5k=15

Chọn B.

Câu 45 (TH) - Công thức lượng giác

Phương pháp:

Cách giải:

P=sin6α+cos6α+msin2α⇔P=(sin2α+cos2α)(sin4α−sin2α.cos2α+cos4α)+msin2α⇔P=sin4α−sin2α.cos2α+cos4α+msin2α⇔P=(sin2α+cos2α)2−3sin2α.cos2α+msin2α⇔P=1−34sin22α+msin2α⇔P=−34sin22α+msin2α+1⇔−34sin22α+msin2α+1−P=0(1)

Phương trình (1) có nghiệm khi và chỉ khi :

 Δ≥0⇔m2−4.(−34).(1−P)≥0⇔m2+3−3P≥0⇔P≤m2+33

Chọn C.

Câu 46 (TH) - Ôn tập đại số

Phương pháp:

Biến đổi S=1x+4y về dạng S=5+4xy+yx sau đó áp dụng bất đẳng thức Cô-si.

Cách giải:

Ta có:

S=1x+4y=1.(1x+4y)=(x+y).(1x+4y)=1+4xy+yx+4=5+4xy+yx

Vì x,y là hai số thực dương nên 4xy,yxdương.

Áp dụng bất đẳng thức Cô-si cho hai số 4xy và yx ta được:

4xy+yx≥2.√4xy.yx⇔4xy+yx≥4⇔5+4xy+yx≥9⇔S≥9

Dấu “=” xảy ra khi và chỉ khi {4xy=yxx+y=1⇔{4x2=y2x+y=1⇔{2x=yx+y=1⇔{x=13y=23

Vậy minS=9⇔x=13;y=23.

Chọn B.

Câu 47 (TH) - Bất phương trình

Phương pháp:

Áp dụng bất đẳng thức (A+B)2=A2+2AB+B2 và A2−B2=(A−B)(A+B) để giải bất phương trình. Từ đó, tìm các giá trị nguyên của x thỏa mãn điều kiện |x|≤2019.

Cách giải:

x4−1>x2+2x⇔x4>x2+2x+1⇔x4>(x+1)2⇔x4−(x+1)2>0⇔(x2−x−1)(x2+x+1)>0⇔x2−x−1>0(dox2+x+1>0,∀x∈R)⇔[x<1−√52x>1+√52⇒x∈(−∞;1−√52)∪(1+√52;+∞)

Ta lại có: |x|≤2019 nên −2019≤x≤2019.

Mà x∈Z.⇒x∈{−2019;−2018;…;−1;2;…;2018;2019}

Do đó, số nghiệm nguyên của bất phương trình là: 2019+2018=4037 (phần tử)

Chọn C.

Câu 48 (TH) - Ôn tập chương 3: Phương pháp tọa độ trong mặt phẳng

Phương pháp:

Gọi →nAB=(u;v) với u2+v2>0.

Chứng minh được: cos(AB,BN)=|→nAB.→nBN||→nAB|.|→nBN| và cos(AB,BN)=BMBN để |→nAB.→nBN||→nAB|.|→nBN|=BMBN

Cách giải:

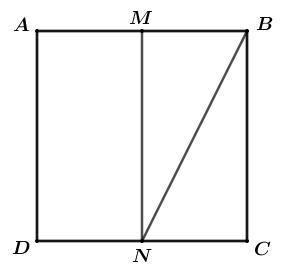
Đường thẳng BN có phương trình 2x+9y−34=0⇒→nBN=(2;9).

Gọi →nAB=(u;v) với u2+v2>0.

⇒cos(AB,BN)=|→nAB.→nBN||→nAB|.|→nBN|=|2a+9b|√22+92.√u2+v2=|2a+9b|√85.√u2+v2  (1)

Xét tam giác BMN vuông tại M ta có:

BN2=BM2+MN2=AB24+AB2=54AB2⇒BN=√52AB

cos(AB,BN)=BMBN=12ABAB.√54=1√5   (2)

Từ (1)  và (2)  ta có:

|2u+9v|√85.√u2+v2=1√5⇔(2u+9v)2=17(u2+v2)⇔4u2+36uv+81v2=17u2+17v2⇔13u2−36uv−64v2=0⇔13u2−52uv+16uv−64v2=0⇔13u(u−4v)+16b(u−4v)=0⇔(u−4v)(13u+16v)=0⇔[u−4v=013u+16v=0⇔[u=4v13u=−16v⇔[u=4vu=−1613v

Trường hợp 1: u=4v⇒→nAB=(4v;v)=(4;1)

PTTQ của đường thẳng đi qua M(−12;2) nhận →nAB=(4;1) là VTPT có dạng là :

4.(x+12)+1.(y−2)=0⇔4x+y=0

Tọa độ điểm B là nghiệm của hệ phương trình:

{2x+9y−34=04x+y=0⇔{2x+9y=344x+y=0⇔{x=−1y=4(tm)

⇒a=−1,b=4

⇒a2+b2=(−1)2+42=17

Trường hợp 2: u=−1613v⇒→nAB=(u=−1613v;v)=(−1613;1)

PTTQ của đường thẳng đi qua M(−12;2) nhận →nAB=(−1613;1) là VTPT có dạng là :

−1613.(x+12)+1.(y−2)=0⇔−1613x+y−3413=0

Tọa độ điểm B là nghiệm của hệ phương trình:

{2x+9y−34=0−1613x+y−3413=0⇔{2x+9y=34−1613x+y=3413⇔{x=45y=185(ktm)

⇒ Loại

Chọn C.

Câu 49 (TH): - Bất phương trình

Phương pháp:

Sử dụng phương pháp giải và biện luận bất phương trình (bất phương trình mx+4>0 có nghiệm đúng khi và chỉ khi hàm số y=mx+4 nằm phía trên trục hoành.

Cách giải:

|x|<8⇔−8<x<8 hay x∈(−8;8).

Bất phương trình mx+4>0 có nghiệm đúng với ∀x∈(−8;8) khi và chỉ khi đồ thị của hàm số y=mx+4 trên khoảng (−8;8) nằm ở phía trên trục hoành và hai đầu mút của đoạn thẳng cũng nằm phía trên trục hoành ⇔{−8m+4≥08m+4≥0⇔{m≤12m≥−12⇔−12≤m≤12.

Vậy m∈[−12;12].

Chọn D.

Câu 50 (TH) - Bất đẳng thức

Phương pháp:

Sử dụng bất đẳng thức x2+y2≥2xy và xy≤(x+y)24.

Cách giải:

(x−y)2≥0⇔x2+y2−2xy≥0⇔x2+y2≥2xy

(x+y)2=x2+2xy+y2≥4xy⇒xy≤(x+y)24

Theo đề bài, ta có:

x2+y2=x+y+xy⇔x+y=(x+y)2−3xy≥(x+y)2−3(x+y)24⇔x+y≥14(x+y)2⇔4(x+y)≥(x+y)2⇔(x+y)2−4(x+y)≤0⇔(x+y)(x+y−4)≤0⇔0≤x+y≤4⇔0≤S≤4

Chọn D.

Đề thi Học kì 2 Toán 10 Kết nối tri thức (Có đáp án) - Đề số 01

Phòng Giáo dục và Đào tạo ...

Đề thi Giữa học kì 2 Toán 10

Năm học 2022 - 2023

Môn: Toán học 10

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

Câu 1. Bất phương trình $ax+b>0$ vô nghiệm khi:

A. $\{\begin{array}{l}a=0\\ b\ne 0\end{array}$ 

B. $\{\begin{array}{l}a=0\\ b\le 0\end{array}$

C. $\{\begin{array}{l}a>0\\ b>0\end{array}$  

D. $\{\begin{array}{l}a\ne 0\\ b=0\end{array}$

Câu 2. Đường thẳng $\left(d\right)$ có phương trình $ax+by+c=0$ với $a^2+b^2>0$. Ta xét $4$ mệnh đề sau:

1. $\overrightarrow{u}\left(b;-a\right)$ là véc tơ chỉ phương của $\left(d\right)$
2. $b=0$ đường thẳng $\left(d\right)$ song song với trục tung
3. $\overrightarrow{n}\left(ka;kb\right),\mathrm{\forall }k\in \mathbb{R}$ là véc tơ pháp tuyến của $\left(d\right)$
4. Nếu $b\ne 0$ đường thẳng $\left(d\right)$ co hệ số góc $k={\displaystyle \frac{-a}{b}}$

Số mệnh đề sai trong các mệnh đề trên:

A. $4$       B. $2$      C. $1$      D. $3$

Câu 3. Phương trình tham số của đường thẳng đi qua $M\left(3;4\right)$ và có véc tơ chỉ phương $\overrightarrow{u}\left(1;-2\right)$ là

A. $\{\begin{array}{l}x=1+3t\\ y=-2+4t\end{array}$ 

B. $\{\begin{array}{l}x=3+t\\ y=4-2t\end{array}$            

C. $\{\begin{array}{l}x=3+4t\\ y=1-2t\end{array}$                                 

D. $\{\begin{array}{l}x=-3+t\\ y=-4-2t\end{array}$

Câu 4. Cho bảng xét dấu:

  

Hàm số có bảng xét dấu như trên là:

A. $f\left(x\right)=16-8x$     B. $f\left(x\right)=x-2$ 

C. $f\left(x\right)=-x-2$       D. $f\left(x\right)=2-4x$

Câu 5. Nếu $a>b>0,c>d>0$ thì bất đẳng thức nào sau đây sai?

A. $ac>bd$    

B. $a-c>b-d$      

C. $a^2>b^2$  

D. $ac>bc$

Câu 6. Tam giác $ABC$ có $a=4,b=6,m_c=4$. Tính độ dài cạnh $c$.

A. $2\sqrt{10}$      

B. ${\displaystyle \frac{\sqrt{10}}{2}}$      

C. $3\sqrt{10}$    

D. $\sqrt{10}$

Câu 7. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số $f\left(x\right)={\displaystyle \frac{x^2+4x+5}{x^2+3x+3}}$ lần lượt là $M$ và $m$ thì:

A. $M+m={\displaystyle \frac{4}{3}}$   B. $M.m={\displaystyle \frac{3}{4}}$                             

C. ${\displaystyle \frac{M}{m}}={\displaystyle \frac{4}{3}}$    D. $M-m={\displaystyle \frac{4}{3}}$

Câu 8. Cho tam thức $f\left(x\right)=a{x}^2+bx+c$ với $a<0$ và $\mathrm{\Delta }=0$. Phát biểu nào sau đây đúng?

A. $f\left(x\right)<0,\mathrm{\forall }x\in R\mathrm{\setminus }\left\{-{\displaystyle \frac{b}{2a}}\right\}$                                       

B. $f\left(x\right)<0,\mathrm{\forall }x\in R$                                        

C. $f\left(x\right)<0,\mathrm{\forall }x\in R\mathrm{\setminus }\left\{-{\displaystyle \frac{b}{a}}\right\}$                                            

D. $f\left(x\right)<0$ khi $x\in \left(-{\displaystyle \frac{b}{2a}};+\mathrm{\infty }\right)$ và $f\left(x\right)>0$ khi $x\in \left(-\mathrm{\infty };-{\displaystyle \frac{b}{2a}}\right)$

Câu 9. Nếu $m>0,n<0$ thì bất đẳng thức nào sau đây luôn đúng?

A. $-m>-n$        B. $mn>0$    C. $m>-n$     D. $n-m<0$

Câu 10. Góc giữa hai đường thẳng $\{\begin{array}{l}x=1+2t\\ y=-2+t\end{array}$ và $\{\begin{array}{l}x=1-3t\\ y=-2+t\end{array}$ là:

A. ${45}^0$       B. ${30}^0$          C. ${135}^0$      D. ${23}^0{13}^{\prime }$

Câu 11. Nếu $0<a<1$ thì bất đẳng thức nào sau đây là đúng?

A. $a^3>a^2$      B. $a>{\displaystyle \frac{1}{a}}$                                   

C. ${\displaystyle \frac{1}{a}}>\sqrt{a}$      D. $a>\sqrt{a}$

Câu 12. Tập xác định của hàm số $y=\sqrt{5-4x-x^2}$ là

A. $\left(-\mathrm{\infty };-5\right]\cup \left[1;+\mathrm{\infty }\right)$         

B. $\left(-\mathrm{\infty };-{\displaystyle \frac{1}{5}}\right]\cup \left[1;+\mathrm{\infty }\right)$   

C. $\left[-5;1\right]$                          

D. $\left[-{\displaystyle \frac{1}{5}};1\right]$

Câu 13. Cho tam giác $ABC$ có $b^2=a^2+c^2+ac$. Số đo của góc $B$ là:

A. ${150}^0$         B. ${30}^0$       C. ${60}^0$       D. ${120}^0$

Câu 14. Tam giác $ABC$ có $AB=12,AC=8$, góc $A$ bằng ${30}^0$. Tính diện tích tam giác đó.

A. $24\sqrt{2}$         B. $48$        C. $24\sqrt{3}$      D. $24$

Câu 15. Số nghiệm nguyên của bất phương trình ${\displaystyle \frac{x^4-x^2}{x^2+5x+6}}\le 0$?

A. $2$       B. $3$        C. $1$           D. $0$

Câu 16. Miền nghiệm của bất phương trình nào sau đây được biểu diễn bởi nửa mặt phẳng không bị gạch trong hình vẽ bên (kể cả bờ là đường thẳng)?

 

A. $x+2y+2\le 0$             

B. $2x+y+2\le 0$              

C. $2x+y\ge -2$               

D. $2x+y-2\ge 0$

Câu 17. Đường thẳng đi qua hai điểm $A\left(3;4\right),B\left(-1;2\right)$ là:

A. $2x+y-5=0$                

B. $x+2y-5=0$                

C. $x-2y+5=0$                

D. $x-2y-1=0$

Câu 18. Tìm tham số $m$ để hàm số $y=\sqrt{\left(m+1\right)x^2-2\left(m+1\right)+4}$ có tập xác định là $D=\mathbb{R}$?

A. $-1\le m\le 3$         

B. $m\ge -1$                                   

C. $-1<m<3$       

D. $-1<m\le 3$

Câu 19. Cho hệ bất phương trình $\{\begin{array}{l}3x-6<0\\ mx+m-1\ge 0\end{array}$. Giá trị của $m$ để hệ bất phương trình vô nghiệm là:

A. $0\le m\le {\displaystyle \frac{1}{3}}$      

B. Kết quả khác                     

C. $m>0$         

D. $m\le {\displaystyle \frac{1}{3}}$

Câu 20. Điểm nào sau đây không thuộc miền nghiệm của hệ bất phương trình $\{\begin{array}{l}2x+3y-1>0\\ 5x-y+4<0\end{array}$?

A. $\left(-1;4\right)$     

B. $\left(-2;4\right)$                          

C. $\left(1;0\right)$       

D. $\left(-3;4\right)$

Câu 21. Tổng các nghiệm của bất phương trình $x\left(3-x\right)\ge x\left(7-x\right)-6\left(x-1\right)$ trên đoạn $\left[-6;6\right]$.

A. $9$           

B. $18$          

C. $12$          

D. $15$

Câu 22. Phương trình $2m{x}^2-2mx+3=0$ vô nghiệm khi và chỉ khi

A. $0<m<6$           

B. $[\begin{array}{l}m<0\\ m>6\end{array}$                                  

C. $0\le m\le 3$          

D. $0\le m<6$

Câu 23. Tập nghiệm của bất phương trình ${\displaystyle \frac{x^2+2x-8}{\left|x+1\right|}}<0$ là:

A. $\left(-2;-1\right)\cup \left(-1;1\right)$                                      

B. $\left(-4;-1\right)\cup \left(-1;2\right)$              

C. $\left(-4;-1\right)$                                                           

D. $\left(-\mathrm{\infty };-4\right)\cup \left(-1;2\right)$

Câu 24. Cho tam giác $ABC$ có $A\left(-1;6\right),B\left(0;2\right),C\left(1;5\right)$. Gọi $\alpha$ là góc giữa hai đường cao $AH$ và $BK$, khi đó:

A. $\cos \alpha ={\displaystyle \frac{1}{\sqrt{2}}}$                  

B. $\cos \alpha ={\displaystyle \frac{7}{5\sqrt{2}}}$                

C. $\cos \alpha ={\displaystyle \frac{-1}{5\sqrt{2}}}$                     

D. $\cos \alpha ={\displaystyle \frac{1}{5\sqrt{2}}}$

Câu 25. Cặp bất phương trình nào sau đây không tương đương?

A. $x^2\left(x+2\right)<0$ và $x+2<0$                                      

B. $2x^2\left(x+1\right)\le 0$ và $x+1\le 0$                                 

C. $\sqrt{x-1}\ge x$ và $\left(2x-1\right)\sqrt{x-1}\ge x\left(2x-1\right)$             

D. $2x+1+{\displaystyle \frac{1}{x-2}}<{\displaystyle \frac{1}{x-2}}$và $2x+1<0$

Câu 26. Cho hai điểm $A\left(1;-2\right),B\left(3;6\right)$. Phương trình đường trung trực của đoạn thẳng $AB$ là:

A. $2x+8y+5=0$             

B. $x+4y+10=0$             

C. $x+4y-10=0$              

D. $2x+8y-5=0$

Câu 27. Số nghiệm nguyên âm của bất phương trình ${\displaystyle \frac{\left|x^2-8x+12\right|}{\sqrt{5-x}}}>{\displaystyle \frac{x^2-8x+12}{\sqrt{5-x}}}$ là

A. $3$       

B. vô số         

C. $2$      

D. $0$

Câu 28. Tìm tất cả các giá trị thực của tham số $m$ để bất phương trình $\left(m^2-4\right)x^2+\left(m-2\right)x+1\le 0$ có nghiệm với mọi $x\in R$.

A. Đáp án khác                                                          

B. $m\in \left(-\mathrm{\infty };2\right)\cup \left({\displaystyle \frac{10}{3}};+\mathrm{\infty }\right)$                                       

C. $m\in \left(-{\displaystyle \frac{10}{3}};-2\right)$

D. $m\in \left(-\mathrm{\infty };2\right)\cup \left[{\displaystyle \frac{10}{3}};+\mathrm{\infty }\right)$

Câu 29. Tìm tất cả các gía trị thực của tham số $m$ sao cho phương trình $\left(m-1\right)x^2-2\left(m+1\right)x+m+4=0$ có hai nghiệm dương phân biệt.

A. $m<-4$ hoặc $1<m<5$                                           

B. $m<-1$ hoặc $-4<m<5$                                                    

C. $1<m<5$                                                          

D. $-4<m<5$

Câu 30. Tập hợp các giá trị của $m$ để $3$ đường thẳng sau đồng quy: $2x-y+1=0$, $x-y+2=0$, $\left(1+m^2\right)x-y+2m-1=0$ là

A. $\left\{1;-3\right\}$         

B. $\left\{1\right\}$                            

C. $\left\{-3\right\}$       

D. Đáp án khác

Lời giải chi tiết

Câu 1 (TH) - Bất phương trình

Phương pháp:

Sử dụng phương pháp biện luận bất phương trình bậc nhất một ẩn.

Cách giải:

Nếu $a=0$ và $b\le 0$ thì bất phương trình vô nghiệm.

Chọn B.

Câu 2 (TH) - Phương trình đường thẳng

Phương pháp:

Xác định VTCP, VTPT, hệ só góc của đường thẳng $d$.

Cách giải:

Đường thẳng $\left(d\right)$ có phương trình $ax+by+c=0$ với $a^2+b^2>0$, ta có:

+) VTPT ${\overrightarrow{n}}_d=\left(a;b\right)\Rightarrow \overrightarrow{u}=\left(b;-a\right)$ là VTCP của $\left(d\right)$

$\Rightarrow$ Mệnh đề $1$ đúng

+) Nếu $b=0$ đường thẳng $\left(d\right)$ trở thành $ax+c=0\Rightarrow x=-{\displaystyle \frac{c}{a}}$

$\Rightarrow$ $x=-{\displaystyle \frac{c}{a}}$ là đường thẳng song song hoặc trùng với trục tung.

$\Rightarrow$ Mệnh đề $2$ sai

+) VTPT ${\overrightarrow{n}}_d=\left(a;b\right)$$\Rightarrow k{\overrightarrow{n}}_d=\left(ka;kb\right),$$\mathrm{\forall }k\ne 0$cũng là VTPT của $\left(d\right)$

$\Rightarrow$ Mệnh đề $3$ sai

+) Nếu $b\ne 0$ ta có: $ax+by+c=0$$\Rightarrow y=-{\displaystyle \frac{a}{b}}x-{\displaystyle \frac{c}{b}}$

$\Rightarrow$ Đường thẳng $\left(d\right)$ có hệ số góc là $k-{\displaystyle \frac{a}{b}}$.

$\Rightarrow$ Mệnh đề $4$ đúng

Vậy có $2$ mệnh đề sai.

Chọn B.

Câu 3 (TH) - Phương trình đường thẳng

Phương pháp:

Phương trình tham số của đường thẳng $\mathrm{\Delta }$ đi qua $M\left(x_0;y_0\right)$ nhận $\overrightarrow{u}=\left(a;b\right)$ là VTCP có dạng

$\{\begin{array}{l}x=x_0+at\\ y=y_0+bt\end{array}\left(t\in \mathbb{R}\right)$

Cách giải:

Phương trình tham số đường thẳng đi qua $M\left(3;4\right)$ và có véc tơ chỉ phương $\overrightarrow{u}\left(1;-2\right)$ là $\{\begin{array}{l}x=3+t\\ y=4-2t\end{array}$

Chọn B.

Câu 4 (TH) - Dấu của nhị thức bậc nhất

Phương pháp:

Hàm số $f\left(x\right)=ax+b$ có giá trị cùng dấu với hệ số $a$ khi $x$ lấy giá trị trong khoảng $\left(-{\displaystyle \frac{b}{a}};+\mathrm{\infty }\right)$, trái dấu với hệ số $a$ khi $x$ lấy giá trị trong khoảng $\left(-\mathrm{\infty };-{\displaystyle \frac{b}{a}}\right)$.

Cách giải:

Đặt $f\left(x\right)=ax+b$ là hàm số cần tìm.

Quan sát bảng xét dấu ta thấy, hàm số có nghiệm là $x=2$.

$\Rightarrow$ Đáp án C và đáp án D sai.

Trong khoảng $\left(2;+\mathrm{\infty }\right)$, hàm số $f\left(x\right)=ax+b$ mang dấu $-$ nên $a<0$.

$\Rightarrow$ Đáp án A đúng và đáp án B sai.

Chọn A.

Câu 5 (TH) - Bất đẳng thức

Phương pháp:

Sử dụng các tính chất cơ bản của bất đẳng thức để chứng minh.

Cách giải:

+) $\{\begin{array}{l}a>b>0\\ c>d>0\end{array}$ $\Rightarrow ac>bd$

 $\Rightarrow$  Đáp án A đúng.

+) Chọn $a=5,b=4,c=3,d=1$ thỏa mãn $a>b>0,c>d>0$.

$\{\begin{array}{l}5>4>0\\ 3>1>0\end{array}$$\Rightarrow 5-3>4-1$ (vô lý)

 $\Rightarrow$  Đáp án B sai.

+) $a>b>0\Rightarrow a^2>b^2$ (vì hai vế của bất đẳng thức luôn dương nên khi bình phương hai vế thì dấu của bất đẳng thức không đổi chiều)

$\Rightarrow$ Đáp án C đúng.

+) $\{\begin{array}{l}a>b>0\\ c>0\end{array}$$\Rightarrow ac>bc$ (nhân cả hai vế của bất đẳng thức $a>b$ với một số $c>0$ thì dấu của BĐT không đổi chiều)

$\Rightarrow$ Đáp án D đúng.

Chọn B.

Câu 6 (TH) - Các hệ thức lượng trong tam giác và giải tam giác

Phương pháp:

Sử dụng công thức tính độ dài đường trung tuyến trong tam giác: $m_c^2={\displaystyle \frac{a^2+b^2}{2}}-{\displaystyle \frac{c^2}{4}}$

Cách giải:

Áp dụng công thức tính độ dài đường trung tuyến của tam giác $ABC$ ta có:

$m_c^2={\displaystyle \frac{a^2+b^2}{2}}-{\displaystyle \frac{c^2}{4}}$

$\begin{array}{l}\iff 4m_c^2=2\left(a^2+b^2\right)-c^2\\ \iff c^2=2\left(a^2+b^2\right)-4m_c^2\end{array}$

Mà $a=4,b=6,m_c=4$ nên ta có: $c^2=2\left(4^2+6^2\right)-{4.4}^2=40$

$\Rightarrow c=\sqrt{40}=2\sqrt{10}$

Chọn A.

Câu 7 (TH) - Phương trình quy về phương trình bậc hai

Phương pháp:

Đặt: ${\displaystyle \frac{x^2+4x+5}{x^2+3x+3}}=A$  $\left(1\right)$ 

Biến đổi $\left(1\right)$về dạng phương trình bậc hai và tìm điều kiện để $\left(1\right)$ có nghiệm. Từ đó tìm được $M$ và $m$.

Cách giải:

Đặt $f\left(x\right)={\displaystyle \frac{x^2+4x+5}{x^2+3x+3}}=A$

$\begin{array}{l}\iff x^2+4x+5=A\left(x^2+3x+3\right)\\ \iff x^2+4x+5-A\left(x^2+3x+3\right)=0\\ \iff x^2+4x+5-A{x}^2-3Ax-3A=0\\ \iff \left(1-A\right)x^2+\left(4-3A\right)x+5-3A=0\left(1\right)\end{array}$

Phương trình $\left(1\right)$ có nghiệm $\iff \mathrm{\Delta }\ge 0$

$\begin{array}{l}\mathrm{\Delta }\ge 0\iff {\left(4-3A\right)}^2\\ -4.\left(1-A\right)\left(5-3A\right)\ge 0\\ \iff \left(16-24A+9A^2\right)\\ -\left(4-4A\right)\left(5-3A\right)\ge 0\\ \iff \left(16-24A+9A^2\right)\\ -\left(20-12A-20A+12A^2\right)\ge 0\\ \iff 16-24A+9A^2-20\\ +12A+20A-12A^2\ge 0\\ \iff -3A^2+8A-4\ge 0\\ \iff 3A^2-8A+4\le 0\\ \iff \left(A-2\right)\left(3A-2\right)\le 0\\ \iff {\displaystyle \frac{2}{3}}\le A\le 2\end{array}$

+) $A\ge {\displaystyle \frac{2}{3}}\Rightarrow MinA={\displaystyle \frac{2}{3}}$

$A={\displaystyle \frac{2}{3}}\iff {\displaystyle \frac{x^2+4x+5}{x^2+3x+3}}={\displaystyle \frac{2}{3}}$$\iff 3x^2+12x+15=2x^2+6x+6$$\iff x^2+6x+9=0$$\iff x=-3$

+) $A\le 2\Rightarrow MaxA=2$

$A=2\iff {\displaystyle \frac{x^2+4x+5}{x^2+3x+3}}=2$$\iff x^2+4x+5=2x^2+6x+6$$\iff x^2+2x+1=0$$\iff x=-1$

Vậy $Minf\left(x\right)=MinA={\displaystyle \frac{2}{3}}\iff x=-1$; $Maxf\left(x\right)=MaxA=2\iff x=-1$

Khi đó, ta có: $\{\begin{array}{l}M=2\\ m={\displaystyle \frac{2}{3}}\end{array}$

$M+m={\displaystyle \frac{8}{3}}$$\Rightarrow$ Đáp án $A$ sai.

$Mm={\displaystyle \frac{4}{3}}$$\Rightarrow$ Đáp án $B$  sai.

${\displaystyle \frac{M}{m}}=3$$\Rightarrow$ Đáp án $C$  sai.

$M-m={\displaystyle \frac{4}{3}}$$\Rightarrow$ Đáp án$D$ đúng.

Chọn D.

Câu 8 (TH) - Dấu của tam thức bậc hai

Phương pháp:

Sử dụng phương pháp biện luận phương trình bậc hai (Nếu $\mathrm{\Delta }=0$ thì $f\left(x\right)$ có nghiệm kép).

Đưa $f\left(x\right)$ về dạng $f\left(x\right)=a{M}^2\left(x\right)$ để xét dấu của $f\left(x\right)$.

Cách giải:

Vì $\mathrm{\Delta }=0$ nên $f\left(x\right)$ có nghiệm kép $x=-{\displaystyle \frac{b}{2a}}$.

$\Rightarrow f\left(x\right)=a{\left(x+{\displaystyle \frac{b}{2a}}\right)}^2$ mà $a<0$ nên $f\left(x\right)=a{\left(x+{\displaystyle \frac{b}{2a}}\right)}^2\le 0$

Dấu “$=$” xảy ra $\iff x=-{\displaystyle \frac{b}{2a}}$.

Do đó, $f\left(x\right)<0,\mathrm{\forall }x\in R\mathrm{\setminus }\left\{-{\displaystyle \frac{b}{2a}}\right\}$

Chọn A.

Câu 9 (TH) - Bất đẳng thức

Phương pháp:

Sử dụng các tính chất cơ bản của bất đẳng thức để chứng minh.

Cách giải:

Nếu $m>0,n<0$ thì $m>n$.

+) Xét đáp án A:

$-m>-n\iff m<n$ (trái với đề bài)

$\Rightarrow$ Đáp án $A$sai.

+) Xét đáp án B:

$mn>0\Rightarrow$$m$ và $n$ cùng dấu (trái với đề bài)

$\Rightarrow$ Đáp án $B$ sai.

+) Xét đáp án C:

Chọn $m=3>0,n=-4<0\Rightarrow 3>-\left(-4\right)$ hay $3>4$ (vô lý)

$\Rightarrow$ Đáp án $C$ sai.

+) Xét đáp án D:

$n-m<0\iff m>n$ (thỏa mãn đề bài)

$\Rightarrow$ Đáp án $D$ đúng.

Chọn D.

Câu 10 (TH) - Tích vô hướng của hai vectơ

Phương pháp:

Công thức tính góc giữa hai đường thẳng: $\cos \phi =\left|\cos \left({\overrightarrow{n}}_1,{\overrightarrow{n}}_2\right)\right|={\displaystyle \frac{\left|{\overrightarrow{n}}_1.{\overrightarrow{n}}_2\right|}{\left|{\overrightarrow{n}}_1\right|.\left|{\overrightarrow{n}}_2\right|}}$ hoặc $\cos \phi =\left|\cos \left({\overrightarrow{u}}_1,{\overrightarrow{u}}_2\right)\right|={\displaystyle \frac{\left|{\overrightarrow{u}}_1.{\overrightarrow{u}}_2\right|}{\left|{\overrightarrow{u}}_1\right|.\left|{\overrightarrow{u}}_2\right|}}$

Cách giải:

$\left(d_1\right):\{\begin{array}{l}x=1+2t\\ y=-2+t\end{array}\Rightarrow {\overrightarrow{u}}_{d_1}=\left(2;1\right)$

$\left(d_2\right):\{\begin{array}{l}x=1-3t\\ y=-2+t\end{array}\Rightarrow {\overrightarrow{u}}_{d_2}=\left(-3;1\right)$

$\mathrm{c}\mathrm{o}\mathrm{s}\left(d_1,d_2\right)=\mathrm{c}\mathrm{o}\mathrm{s}\left({\overrightarrow{u}}_{d_1},{\overrightarrow{u}}_{d_2}\right)$$={\displaystyle \frac{\left|{\overrightarrow{u}}_{d_1}.{\overrightarrow{u}}_{d_2}\right|}{\left|{\overrightarrow{u}}_{d_1}\right|.\left|{\overrightarrow{u}}_{d_2}\right|}}$$={\displaystyle \frac{\left|2.\left(-3\right)+1.1\right|}{\sqrt{2^2+1^2}.\sqrt{{\left(-3\right)}^2+1^2}}}$$={\displaystyle \frac{5}{\sqrt{5}.\sqrt{10}}}={\displaystyle \frac{1}{\sqrt{2}}}$

$\Rightarrow \left(d_1,d_2\right)={45}^0$

Vậy góc giữa hai đường thẳng trên bằng ${45}^0$.

Chọn A.

Câu 11 (TH) - Bất đẳng thức

Phương pháp:

Sử dụng các tính chất cơ bản của bất đẳng thức để chứn minh.

Cách giải:

+) Xét đáp án A:

$$\begin{gathered} a^3>a^2\iff a^3-a^2>0 \\ \iff a^2\left(a-1\right)>0\iff \{\begin{array}{l}{a}^2>0\\ a-1>0\end{array} \\ \iff a>1 \end{gathered}$$(trái với đề bài)

$\Rightarrow$ Đáp án $A$sai.

+) Xét đáp án B:

$a>{\displaystyle \frac{1}{a}}$$\iff {\displaystyle \frac{a^2-1}{a}}>0$ $\iff [\begin{array}{l}\{\begin{array}{l}{a}^2-1>0\\ a>0\end{array}\\ \{\begin{array}{l}{a}^2-1<0\\ a<0\end{array}\end{array}$$\iff [\begin{array}{l}\{\begin{array}{l}[\begin{array}{l}a>1\\ a<-1\end{array}\\ a>0\end{array}\\ \{\begin{array}{l}-1<a<1\\ a<0\end{array}\end{array}$$\iff [\begin{array}{l}a>1\\ -1<a<0\end{array}$ (trái với đề bài)

$\Rightarrow$ Đáp án $B$sai.

+) Xét đáp án C:

${\displaystyle \frac{1}{a}}>\sqrt{a}$ $\iff {\displaystyle \frac{1-a\sqrt{a}}{a}}>0$$\iff \{\begin{array}{l}a>0\\ a\sqrt{a}<1\end{array}$$\iff \{\begin{array}{l}a>0\\ {\left(a\sqrt{a}\right)}^2<1^2\end{array}$$\iff \{\begin{array}{l}a>0\\ a^3<1\end{array}\iff \{\begin{array}{l}a>0\\ a<1\end{array}$$\iff 0<a<1$ (thỏa mãn đề bài)

$\Rightarrow$ Đáp án $C$ đúng.

+) Xét đáp án D:

$a>\sqrt{a}\iff \{\begin{array}{l}a\ge 0\\ a^2>a\end{array}$ $\iff \{\begin{array}{l}a\ge 0\\ a\left(a-1\right)>0\end{array}$$\iff \{\begin{array}{l}a\ge 0\\ [\begin{array}{l}\{\begin{array}{l}a>0\\ a>1\end{array}\\ \{\begin{array}{l}a<0\\ a<1\end{array}\end{array}\end{array}$$\iff \{\begin{array}{l}a\ge 0\\ [\begin{array}{l}a>1\\ a<0\end{array}\end{array}$$\iff a>1$ (trái với đề bài)

$\Rightarrow$ Đáp án $D$ sai.

Chọn C.

Câu 12 (TH) - Tập xác định của hàm số

Phương pháp:

Hàm số $y=\sqrt{f\left(x\right)}$ xác định khi và chỉ khi $f\left(x\right)\ge 0$.

Cách giải:

Hàm số $y=\sqrt{5-4x-x^2}$ xác định khi và chỉ khi $5-4x-x^2\ge 0$.

Ta có bảng xét dấu:

 

Vậy tập xác định của hàm số $y=\sqrt{5-4x-x^2}$ là $\left[-5;1\right]$.

Chọn C.

Câu 13 (TH) - Các hệ thức lượng trong tam giác và giải tam giác

Phương pháp:

Sử dụng hệ quả của định lý cô-sin trong tam giác: $\cos B={\displaystyle \frac{c^2+a^2-b^2}{2ac}}$

Cách giải:

Theo đề bài, ta có:

$b^2=a^2+c^2+ac$ $\Rightarrow b^2=a^2+c^2-2.\left(-{\displaystyle \frac{1}{2}}\right).ac$$\Rightarrow -{\displaystyle \frac{1}{2}}={\displaystyle \frac{a^2+c^2-b^2}{2ac}}$

Mà $\cos B={\displaystyle \frac{a^2+c^2-b^2}{2ac}}$$\Rightarrow \cos B=-{\displaystyle \frac{1}{2}}$$\Rightarrow \mathrm{\angle }B={120}^0$.

Chọn D.

Câu 14 (TH) - Các hệ thức lượng trong tam giác và giải tam giác

Phương pháp:

Sử dụng công thức: $S={\displaystyle \frac{1}{2}}ab\sin C$$={\displaystyle \frac{1}{2}}bc\sin A$$={\displaystyle \frac{1}{2}}ca\sin B$

Cách giải:

Áp dụng công thức tính diện tích, ta có:

$S_{\mathrm{\Delta }ABC}={\displaystyle \frac{1}{2}}.AB.AC.\sin A$$={\displaystyle \frac{1}{2}}.12.8.\sin {30}^0=24$

Chọn D.

Câu 15 (TH) - Bất phương trình

Phương pháp:

Giải bất phương trình để tìm tập nghiệm và tìm các giá trị nguyên nằm trong tập nghiệm đó.

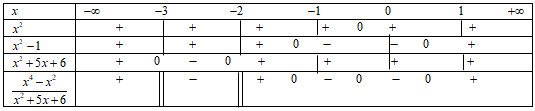
Cách giải:

ĐKXĐ: $x^2+5x+6\ne 0\iff \{\begin{array}{l}x\ne -2\\ x\ne -3\end{array}$

${\displaystyle \frac{x^4-x^2}{x^2+5x+6}}\le 0\iff {\displaystyle \frac{x^2\left(x^2-1\right)}{x^2+5x+6}}\le 0$

Ta có bảng xét dấu:

$\Rightarrow x\in \left(-3;-2\right)\cup \left[-1;1\right]$

Mà $x\in \mathbb{Z}$ nên $x\in \left\{-1;0;1\right\}$.

Vậy phương trình có $3$ nghiệm nguyên.

Chọn B.

Câu 16 (TH) - Phương trình đường thẳng

Phương pháp:

Viết phương trình đường thẳng đi qua hai điểm $\left(-1;0\right)$ và $\left(0;-2\right)$. Từ đó, dựa vào đồ thị để kết luận bất phương trình.

Cách giải:

Đường thẳng đi qua hai điểm $\left(-1;0\right)$ và $\left(0;-2\right)$ $\Rightarrow VTCP\overrightarrow{\underset{d}{u}}=\left(1;-2\right)$ $\Rightarrow VTPT{\overrightarrow{n}}_d=\left(2;1\right)$

 

$\Rightarrow$Miền nghiệm không bị gạch biểu diễn BPT $2x+y+2\le 0$

Chọn B.

Câu 17 (TH) - Phương trình đường thẳng

Phương pháp:

Tìm VTCP và suy ra VTPT của $AB$.

Phương trình đường thẳng $AB$ đi qua $A\left(x_0;y_0\right)$, nhận $\overrightarrow{n}=\left(a;b\right)$ có dạng: $a\left(x-x_0\right)+b\left(y-y_0\right)=0$

Cách giải:

$A\left(3;4\right),B\left(-1;2\right)$$\Rightarrow \overrightarrow{AB}=\left(-4;-2\right)=\left(2;1\right)$$\Rightarrow {\overrightarrow{n}}_{AB}=\left(1;-2\right)$

Phương trình đường thẳng $AB$ đi qua $A\left(3;4\right)$ có VTPT ${\overrightarrow{n}}_{AB}=\left(1;-2\right)$ là :

$\begin{array}{l}1.\left(x-3\right)-2.\left(y-4\right)=0\\ \iff x-3-2y+8=0\\ \iff x-2y+5=0\end{array}$

Chọn C.

Câu 18 (TH) - Tập xác định của hàm số

Phương pháp:

Hàm số $y=\sqrt{f\left(x\right)}$ có tập xác định là $D=R$ khi và chỉ khi $f\left(x\right)\ge 0$ với $\mathrm{\forall }x\in \mathbb{R}\iff \{\begin{array}{l}a>0\\ \mathrm{\Delta }\le 0\end{array}$.

Cách giải:

Hàm số $y=\sqrt{\left(m+1\right)x^2-2\left(m+1\right)x+4}$ có tập xác định là $D=\mathbb{R}$ khi và chỉ khi $\left(m+1\right)x^2-2\left(m+1\right)x+4\ge 0$ với mọi $x\in \mathbb{R}$.

$\begin{array}{l}\Rightarrow \{\begin{array}{l}a>0\\ \mathrm{\Delta }\le 0\end{array}\\ \iff \{\begin{array}{l}m+1>0\\ 4{\left(m+1\right)}^2-16\left(m+1\right)\le 0\end{array}\\ \iff \{\begin{array}{l}m>-1\\ 4m^2-8m-12\le 0\end{array}\\ \iff \{\begin{array}{l}m>-1\\ -1\le m\le 3\end{array}\\ \iff -1<m\le 3\end{array}$

Chọn D.

Câu 19 (TH) - Bất phương trình và hệ bất phương trình một ẩn

Phương pháp:

Sử dụng phương pháp giải và biện luận bất phương trình.

Cách giải:

$\{\begin{array}{l}3x-6<0\\ mx+m-1\ge 0\end{array}\iff \{\begin{array}{l}x<2\\ mx\ge 1-m\end{array}$

TH1: $m=0$

Hệ bất phương trình trở thành $\{\begin{array}{l}x<0\\ 0\ge 1\end{array}$  (vô lý)

$\Rightarrow$ Hệ bất phương trình vô nghiệm với $m=0$

TH2: $m\ne 0$

Hệ bất phương trình trở thành  $\{\begin{array}{l}x<2\\ mx\ge 1-m\end{array}$$\iff \{\begin{array}{l}x<2\\ x\ge {\displaystyle \frac{1-m}{m}}\end{array}$

Hệ bất phương trình vô nghiệm $\iff {\displaystyle \frac{1-m}{m}}\ge 2$$\iff {\displaystyle \frac{1-3m}{m}}\ge 0$$\iff [\begin{array}{l}\{\begin{array}{l}1-3m\ge 0\\ m>0\end{array}\\ \{\begin{array}{l}1-3m\le 0\\ m<0\end{array}\end{array}$$\iff [\begin{array}{l}\{\begin{array}{l}m\le {\displaystyle \frac{1}{3}}\\ m>0\end{array}\\ \{\begin{array}{l}m\ge {\displaystyle \frac{1}{3}}\\ m<0\end{array}\end{array}$$\iff 0<m\le {\displaystyle \frac{1}{3}}$.

Kết hợp 2 trường hợp ta được: $0\le m\le {\displaystyle \frac{1}{3}}$

Chọn A.

Câu 20 (TH) - Bất phương trình và hệ bất phương trình một ẩn

Phương pháp:

Thay từng điểm vào hệ bất phương trình. Nếu thỏa mãn thì điểm đó thuộc miền nghiệm của hệ bất phương trình.

Cách giải:

+) Với $\left(x;y\right)=\left(-1;4\right)$ bất phương trình trở thành $\{\begin{array}{l}2.\left(-1\right)+3.4-1>0\\ 5.\left(-1\right)-4+4<0\end{array}$$\iff \{\begin{array}{l}9>0\\ -5<0\end{array}$ (thỏa mãn)

$\Rightarrow$ Điểm $\left(-1;4\right)$ thuộc miền nghiệm của hệ bất phương trình $\{\begin{array}{l}2x+3y-1>0\\ 5x-y+4<0\end{array}$

+) Với $\left(x;y\right)=\left(-2;4\right)$ bất phương trình trở thành $\{\begin{array}{l}2.\left(-2\right)+3.4-1>0\\ 5.\left(-2\right)-4+4<0\end{array}$$\iff \{\begin{array}{l}7>0\\ -10<0\end{array}$(thỏa mãn)

$\Rightarrow$ Điểm $\left(-2;4\right)$ thuộc miền nghiệm của hệ bất phương trình $\{\begin{array}{l}2x+3y-1>0\\ 5x-y+4<0\end{array}$

+) Với $\left(x;y\right)=\left(1;0\right)$ bất phương trình trở thành $\{\begin{array}{l}2.1+3.0-1>0\\ 5.1-0+4<0\end{array}$$\iff \{\begin{array}{l}1>0\\ 9<0\end{array}$(vô lý)

$\Rightarrow$ Điểm $\left(1;0\right)$ không thuộc miền nghiệm của hệ bất phương trình $\{\begin{array}{l}2x+3y-1>0\\ 5x-y+4<0\end{array}$

+) Với $\left(x;y\right)=\left(-3;4\right)$ bất phương trình trở thành $\{\begin{array}{l}2.\left(-3\right)+3.4-1>0\\ 5.\left(-3\right)-4+4<0\end{array}$$\iff \{\begin{array}{l}5>0\\ -15<0\end{array}$(thỏa mãn)

$\Rightarrow$ Điểm $\left(-3;4\right)$ thuộc miền nghiệm của hệ bất phương trình $\{\begin{array}{l}2x+3y-1>0\\ 5x-y+4<0\end{array}$

Chọn C.

Câu 21 (TH) - Bất phương trình

Phương pháp:

Giải bất phương trình, tìm các giá trị nguyên của $x$ là nghiệm của bất phương trình và thỏa mãn $\left[-6;6\right]$.

Cách giải:

$\begin{array}{l}x\left(3-x\right)\ge x\left(7-x\right)-6\left(x-1\right)\\ \iff 3x-x^2\ge 7x-x^2-6x+6\\ \iff 3x-7x+6x-6\ge 0\\ \iff 2x-6\ge 0\\ \iff 2x\ge 6\\ \iff x\ge 3\end{array}$

 Kết hợp điều kiện đề bài $x\in \left[-6;6\right]$$\Rightarrow x\in \left[3;6\right]$.

Tổng tất cả các giá trị nguyên của $x$ thỏa mãn $\left[-6;6\right]$ là: $3+4+5+6=18$

Chọn B.

Câu 22 (TH) - Dấu của tam thức bậc hai

Phương pháp:

Xét hai trường hợp: $2m=0$ và $2m\ne 0$ và sử dụng điều kiện vô nghiệm của phương trình bậc hai $\mathrm{\Delta }<0$.

Cách giải:

+) Với $m=0$, phương trình trở thành $3=0$ (vô lý)

$\Rightarrow$ Phương trình $2m{x}^2-2mx+3=0$ vô nghiệm khi $m=0$ $\left(1\right)$

+) Với $m\ne 0$:

Phương trình $2m{x}^2-2mx+3=0$ vô nghiệm$$\begin{gathered} \iff \mathrm{\Delta }<0\iff 4m^2-24m<0 \\ \iff 4m\left(m-6\right)<0\iff 0<m<6 \end{gathered}$$$\left(2\right)$

Kết hợp $\left(1\right)$và $\left(2\right)$ta được: $0\le m<6$

Chọn D.

Câu 23 (TH) - Bất phương trình

Phương pháp:

Phá dấu giá trị tuyệt đối và giải bất phương trình.

Cách giải:

ĐKXĐ: $x\ne -1$

TH1: $x+1>0\iff x>-1$

$\Rightarrow \left|x+1\right|=x+1$

$\begin{array}{l}\mathrm{BPT}\iff {\displaystyle \frac{x^2+2x-8}{x+1}}<0\\ \iff \{\begin{array}{l}{x}^2+2x-8<0\\ x+1>0\end{array}\\ \iff \{\begin{array}{l}-4<x<2\\ x>-1\end{array}\\ \iff -1<x<2\end{array}$

TH2: $x+1<0\iff x<-1$

$\Rightarrow \left|x+1\right|=-\left(x+1\right)$

$\begin{array}{l}\mathrm{BPT}\iff {\displaystyle \frac{x^2+2x-8}{-\left(x+1\right)}}<0\\ \iff \{\begin{array}{l}{x}^2+2x-8<0\\ x+1<0\end{array}\\ \iff \{\begin{array}{l}-4<x<2\\ x<-1\end{array}\\ \iff -4<x<-1\end{array}$

Kết hợp $2$ trường hợp trên, tập nghiệm của bất phương trình là $\left(-4;-1\right)\cup \left(-1;2\right)$.

Chọn B.

Câu 24 (TH) - Tích vô hướng của hai vectơ

Phương pháp:

Xác định VTPT của $AH$ và $BK$.

Áp dụng công thức: $\cos \left({\overrightarrow{n}}_{AH},{\overrightarrow{n}}_{BK}\right)={\displaystyle \frac{\left|{\overrightarrow{n}}_{AH}.{\overrightarrow{n}}_{BK}\right|}{\left|{\overrightarrow{n}}_{AH}\right|.\left|{\overrightarrow{n}}_{BK}\right|}}$

Cách giải:

$A\left(-1;6\right),B\left(0;2\right),C\left(1;5\right)$$\Rightarrow \overrightarrow{BC}=\left(1;3\right),\overrightarrow{AC}=\left(2;-1\right)$

Vì $AH\mathrm{\perp }BC$ nên $\overrightarrow{BC}$ là VTPT của đường thẳng $AH$ suy ra ${\overrightarrow{n}}_{AH}=\overrightarrow{BC}=\left(1;3\right)$.

Vì $BK\mathrm{\perp }AC$ nên $\overrightarrow{AC}$ là VTPT của đường thẳng $BK$ suy ra ${\overrightarrow{n}}_{BK}=\overrightarrow{AC}=\left(2;-1\right)$.

$\Rightarrow \cos \alpha =\cos \left({\overrightarrow{n}}_{AH},{\overrightarrow{n}}_{BK}\right)$$={\displaystyle \frac{\left|{\overrightarrow{n}}_{AH}.{\overrightarrow{n}}_{BK}\right|}{\left|{\overrightarrow{n}}_{AH}\right|.\left|{\overrightarrow{n}}_{BK}\right|}}$$={\displaystyle \frac{\left|1.2+3.\left(-1\right)\right|}{\sqrt{1^2+3^2}.\sqrt{2^2+{\left(-1\right)}^2}}}$$={\displaystyle \frac{1}{\sqrt{50}}}={\displaystyle \frac{1}{5\sqrt{2}}}$

Chọn D.

Câu 25 (TH) - Bất phương trình

Phương pháp:

Hai bất phương trình được gọi là tương đương nếu nó có cùng tập nghiệm.

Cách giải:

*) Xét đáp án A

$x^2\left(x+2\right)<0$ $\iff \{\begin{array}{l}{x}^2>0\\ x+2<0\end{array}$$\iff \{\begin{array}{l}x\ne 0\\ x<-2\end{array}$$\iff x<-2$

$x+2<0\iff x<-2$

$\Rightarrow$ Cặp bất phương trình $x^2\left(x+2\right)<0$ và $x+2<0$ tương đương.

*) Xét đáp án B

$2x^2\left(x+1\right)\le 0$ $\iff \{\begin{array}{l}2x^2\ge 0\\ x+1\le 0\end{array}$$\iff [\begin{array}{l}x=0\\ x\le -1\end{array}$

$x+1\le 0\iff x\le -1$

$\Rightarrow$ Cặp bất phương trình $2x^2\left(x+1\right)\le 0$ và $x+1\le 0$ không tương đương 

*) Xét đáp án C:

ĐKXĐ: $x\ge 1$

Vì $x\ge 1\iff 2x\ge 2$$\iff 2x-1\ge 1>0$.

 Khi đó, ta có:

$\left(2x-1\right)\sqrt{x-1}\ge x\left(2x-1\right)$$\iff \sqrt{x-1}\ge x$

$\Rightarrow$ Cặp bất phương trình $\sqrt{x-1}\ge x$ và $\left(2x-1\right)\sqrt{x-1}\ge x\left(2x-1\right)$ tương đương

*) Xét đáp án D:

$2x+1+{\displaystyle \frac{1}{x-2}}<{\displaystyle \frac{1}{x-2}}$$\iff \{\begin{array}{l}x-2\ne 0\\ 2x+1<0\end{array}$$\iff \{\begin{array}{l}x\ne 2\\ x<-{\displaystyle \frac{1}{2}}\end{array}$$\iff x<-{\displaystyle \frac{1}{2}}$

$2x+1<0\iff x<-{\displaystyle \frac{1}{2}}$

$\Rightarrow$ Cặp bất phương trình $2x+1+{\displaystyle \frac{1}{x-2}}<{\displaystyle \frac{1}{x-2}}$và $2x+1<0$ tương đương.

Chọn B.

Câu 26 (TH) - Phương trình đường thẳng

Phương pháp:

Phương trình đường trung trực của đoạn thẳng $AB$ đi qua trung điểm của $AB$ và nhận $\overrightarrow{AB}$ là VTPT.

Cách giải:

Gọi $M\left(x_M;y_M\right)$ là trung điểm của $AB$

$\begin{array}{l}\Rightarrow \{\begin{array}{l}{x}_M={\displaystyle \frac{x_A+x_B}{2}}\\ y_M={\displaystyle \frac{y_A+y_B}{2}}\end{array}\\ \iff \{\begin{array}{l}{x}_M={\displaystyle \frac{1+3}{2}}\\ y_M={\displaystyle \frac{-2+6}{2}}\end{array}\\ \iff \{\begin{array}{l}{x}_M=2\\ y_M=2\end{array}\Rightarrow M\left(2;2\right)\end{array}$

$A\left(1;-2\right),B\left(3;6\right)\Rightarrow \overrightarrow{AB}=\left(2;8\right)$

Giả sử $d$ là đường trung trực của $AB$.

$\Rightarrow$ $d$ đi qua $M\left(2;2\right)$ nhận $\overrightarrow{AB}=\left(2;8\right)$ là VTPT.

$\Rightarrow$ PTTQ của $d$ là: $2.\left(x-2\right)+8.\left(y-2\right)=0$$\iff x+4y-10=0$

Chọn C.

Câu 27 (TH) - Bất phương trình

Phương pháp:

Tìm ĐKXĐ và áp dụng nếu $\left|a\right|>a$ thì $a<0$.

Cách giải:

ĐKXĐ: $5-x>0\iff x<5$

${\displaystyle \frac{\left|x^2-8x+12\right|}{\sqrt{5-x}}}>{\displaystyle \frac{x^2-8x+12}{\sqrt{5-x}}}$      

$\iff \left|x^2-8x+12\right|>x^2-8x+12$

$\begin{array}{l}\iff x^2-8x+12<0\\ \iff 2<x<6\end{array}$

Kết hợp với ĐKXĐ suy ra bất phương trình đã cho có nghiệm $x\in \left(2;5\right)$.

Mà $x\in \mathbb{Z}\Rightarrow x\in \left\{3;4\right\}$.

Vậy bất phương trình đã cho không có nghiệm nguyên âm.

Chọn D.

Câu 28 (TH) - Bất phương trình

 Phương pháp:

Bất phương trình $\left(m^2-4\right)x^2+\left(m-2\right)x+1\le 0$ có nghiệm với mọi $x\in R$  $\iff \{\begin{array}{l}a<0\\ \mathrm{\Delta }\le 0\end{array}$

Cách giải:

Bất phương trình $\left(m^2-4\right)x^2+\left(m-2\right)x+1\le 0$ có nghiệm với mọi $x\in R$  $\iff \{\begin{array}{l}a<0\\ \mathrm{\Delta }\le 0\end{array}$

+) $a<0\iff m^2-4<0\iff -2<m<2$

+)$$\begin{gathered} \mathrm{\Delta }\le 0 \\ \iff {\left(m-2\right)}^2-4.\left(m^2-4\right).1\le 0 \\ \iff -3m^2-4m+20\le 0 \\ \iff [\begin{array}{l}m\le {\displaystyle \frac{-10}{3}}\\ m\ge 2\end{array} \end{gathered}$$

Vậy không có giá trị của $m$ để bất phương trình có nghiệm với mọi $x\in R$.

Chọn A.

Câu 29 (VD) - Phương trình bậc hai

Phương pháp:

Phương trình bậc hai có hai nghiệm dương phân biệt khi và chỉ khi $\{\begin{array}{l}a\ne 0\\ \mathrm{\Delta }>0\\ P>0\\ S>0\end{array}$

Cách giải:

Phương trình $\left(m-1\right)x^2-2\left(m+1\right)x+m+4=0$ có hai nghiệm dương phân biệt khi và chỉ khi

$\{\begin{array}{l}a\ne 0\\ \mathrm{\Delta }>0\\ x_1{x}_2>0\\ x_1+x_2>0\end{array}$$\iff \{\begin{array}{l}m-1\ne 0\left(1\right)\\ 4{\left(m+1\right)}^2-4\left(m-1\right)\left(m+4\right)>0\left(2\right)\\ {\displaystyle \frac{m+4}{m-1}}>0\left(3\right)\\ {\displaystyle \frac{m+1}{m-1}}>0\left(4\right)\end{array}$

Giải $\left(1\right)$: $m-1\ne 0\iff m\ne 1$

Giải $\left(2\right)$:

$\begin{array}{l}4{\left(m+1\right)}^2-4\left(m-1\right)\left(m+4\right)>0\\ \iff \left(4m^2+8m+4\right)\\ -\left(4m-4\right)\left(m+4\right)>0\\ \iff 4m^2+8m+4-4m^2-16m\\ +4m+16>0\\ \iff -4m+20>0\\ \iff m<5\end{array}$

Giải $\left(3\right)$:

${\displaystyle \frac{m+4}{m-1}}>0$$\iff [\begin{array}{l}\{\begin{array}{l}m+4>0\\ m-1>0\end{array}\\ \{\begin{array}{l}m+4<0\\ m-1<0\end{array}\end{array}$$\iff [\begin{array}{l}\{\begin{array}{l}m>-4\\ m>1\end{array}\\ \{\begin{array}{l}m<-4\\ m<1\end{array}\end{array}$$\iff [\begin{array}{l}m>1\\ m<-4\end{array}$

Giải $\left(4\right)$:

${\displaystyle \frac{m+1}{m-1}}>0$$\iff [\begin{array}{l}\{\begin{array}{l}m+1>0\\ m-1>0\end{array}\\ \{\begin{array}{l}m+1<0\\ m-1<0\end{array}\end{array}$$\iff [\begin{array}{l}\{\begin{array}{l}m>-1\\ m>1\end{array}\\ \{\begin{array}{l}m<-1\\ m<1\end{array}\end{array}$$\iff [\begin{array}{l}m>1\\ m<-1\end{array}$

Kết hợp cả $4$ điều kiện ta được $m<-4$ hoặc $1<m<5$.

Chọn A.

Câu 30 (TH) - Phương trình đường thẳng

Phương pháp:

$\left(d_1\right),\left(d_2\right),\left(d_3\right)$ đồng quy nếu $\{\begin{array}{l}{d}_1\cap d_2=\left\{A\right\}\\ A\in \left(d_3\right)\end{array}$

(xác định giao điểm của hai đường thẳng sau đó chứng minh giao điểm đó nằm trên đường thẳng thứ ba)

Cách giải:

$\left(d_1\right):2x-y+1=0$, $\left(d_{{}^2}\right):x-y+2=0$, $\left(d_{{}^3}\right):\left(1+m^2\right)x-y+2m-1=0$

Gọi $\left(d_1\right)\cap \left(d_2\right)=A\left(x_A;y_A\right)$. Tọa độ điểm $A\left(x_A;y_A\right)$ là nghiệm của hệ phương trình:

$\begin{array}{l}\{\begin{array}{l}2x_A-y_A+1=0\\ x_A-y_A+2=0\end{array}\iff \{\begin{array}{l}2x_A-y_A=-1\\ x_A-y_A=-2\end{array}\\ \iff \{\begin{array}{l}{x}_A=1\\ y_A=3\end{array}\Rightarrow A\left(1;3\right)\end{array}$

Để $\left(d_1\right),\left(d_2\right),\left(d_3\right)$ đồng quy thì $A\left(1;3\right)\in \left(d_3\right):\left(1+m^2\right)x-y$$+2m-1=0$.

$\begin{array}{l}\Rightarrow \left(1+m^2\right).1-3+2m-1=0\\ \iff 1+m^2-3+2m-1=0\\ \iff m^2+2m-3=0\\ \iff \left(m-1\right)\left(m+3\right)=0\\ \iff [\begin{array}{l}m-1=0\\ m+3=0\end{array}\iff [\begin{array}{l}m=1\\ m=-3\end{array}\end{array}$

Vậy $m\in \left\{1;-3\right\}$.

Chọn A.

Để xem trọn bộ Đề thi Toán lớp 10 Chân trời sáng tạo có đáp án, Thầy/ cô vui lòng Tải xuống!

Xem thêm đề thi các môn lớp 10 bộ sách Chân trời sáng tạo hay, có đáp án chi tiết:

Top 10 đề thi giữa Học kì 2 Ngữ văn 10 (Chân trời sáng tạo 2024) có đáp án

Top 10 đề thi giữa Học kì 2 Vật lí 10 (Chân trời sáng tạo 2024) có đáp án

Top 10 đề thi giữa Học kì 2 Hóa 10 (Chân trời sáng tạo 2024) có đáp án

Top 50 Đề thi Giữa học kì 2 Lịch sử lớp 10 (Chân trời sáng tạo 2024) tải nhiều nhất