Toptailieu.vn biên soạn và giới thiệu Top 20 Đề thi Giữa học kì 1 Toán 10 (Cánh diều 2023) có đáp án gồm các đề thi được tuyển chọn và tổng hợp từ các đề thi môn Toán THPT trên cả nước có hướng dẫn giải chi tiết giúp học sinh làm quen với các dạng đề, ôn luyện để đạt kết quả cao trong kì thi sắp tới. Mời các bạn đón xem:

Top 20 Đề thi Giữa học kì 1 Toán 10 (Cánh diều 2023) có đáp án

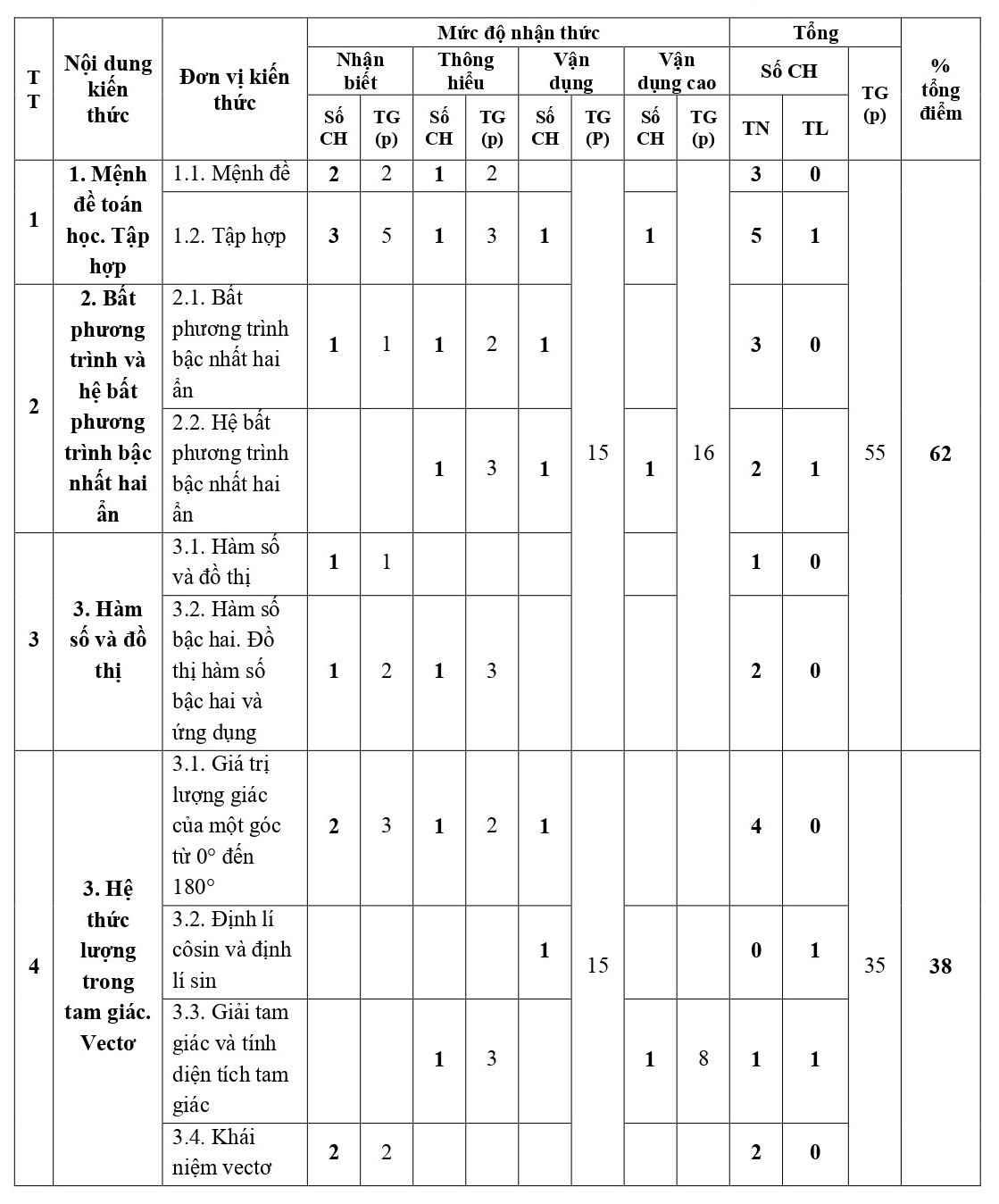
A. MA TRẬN ĐỀ THI GIỮA KỲ 1 TOÁN 10 CÁNH DIỀU (Có đáp án) - ĐỀ SỐ 01

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Giữa Học kì 1

Năm học 2022 - 2023

Môn: Toán 10

Thời gian làm bài: 90 phút

Đề thi Giữa kì 1 Toán 10 Cánh diều (Có đáp án) - Đề số 01

 

I. PHẦN TRẮC NGHIỆM

Câu 1: Trong các câu dưới đây, câu nào là mệnh đề ?

A. Hà Nội là thủ đô của Việt Nam.              

B. Hôm nay là thứ mấy ?

C. Mệt quá !                                      

D. Mấy giờ rồi ?

Câu 2: Trong các mệnh đề dưới đây, mệnh đề nào đúng ?

A. 5 là số tự nhiên chẵn;          

B. 5 là số nguyên tố;

C. 5 là số nguyên âm;                                 

D. 5 là số chia hết cho 3.

Câu 3: Cho tập hợp A = {1; 3; 5; 7; 9}. Số phần tử của tập hợp A là

A. 6;                    

B. 4;                    

C. 5;                    

D. 3.

Câu 4: Cho tập hợp $B=\left\{\left.x\in ℝ\right|a\le x<b\right\}.$ Mệnh đề nào dưới đây đúng ?

A. B = [a; b];        

B. B = (a; b];        

C. B = [a; b) ;        

D. B = (a; b).

Câu 5: Tập xác định của hàm số $f\left(x\right)=\sqrt{x-2}$ là

A. D = [2; +∞);    

B. D = (2; +∞);    

C. D = (– ∞; 2);    

D. D = (– ∞; 2].

Câu 6: Trong mặt phẳng Oxy, điểm nào dưới đây thuộc đồ thị của hàm số $y=\sqrt{x}?$

A. P(4; 2);  

B. M(1; – 1);        

C. N(2; 4);           

D. Q(2; – 4).

Câu 7: Cho hàm số f(x) = x³ – 2. Giá trị f(1) bằng bao nhiêu?

A. 3;           

B. – 1;                  

C. 2; 

D. 1

Câu 8: Hàm số nào dưới đây có đồ thị là đường thẳng như trong hình bên ?

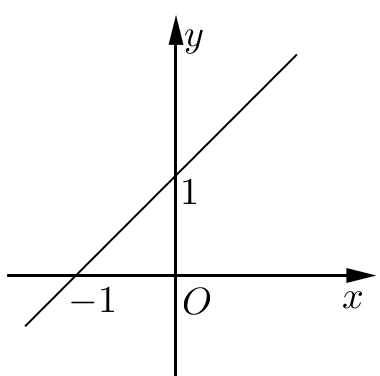
A. y = x + 1;

B. y = x – 1;

C. y = – x + 1;

D. y = – x – 1.

Câu 9: Trong các mệnh đề dưới đây, mệnh đề nào đúng ?

A. Đồ thị hàm số chẵn nhận đường thẳng y = x làm trục đối xứng.

B. Đồ thị hàm số chẵn nhận trục hoành làm trục đối xứng.

C. Đồ thị hàm số chẵn nhận nhận đường thẳng y = – x làm trục đối xứng.

D. Đồ thị hàm số chẵn nhận trục tung làm trục đối xứng.

Câu 10: Trong mặt phẳng Oxy, biết điểm M(2; y₀) thuộc đồ thị của hàm số y = 2x – 3. Giá trị của y₀ bằng:

A. 2;                    

B. 0;                    

C. – 1;        

D. 1.

Câu 11: Trong mặt phẳng Oxy đồ thị của hàm số y = x² – 2x + 3 có trục đối xứng là đường thẳng nào dưới đây ?

A. x = 1;              

B. x = – 1;            

C. x = 2;               

D. x = – 2.

Câu 12: Cho các vectơ $\overrightarrow{u},\overrightarrow{v},\overrightarrow{x},\overrightarrow{y}$ như trong hình:

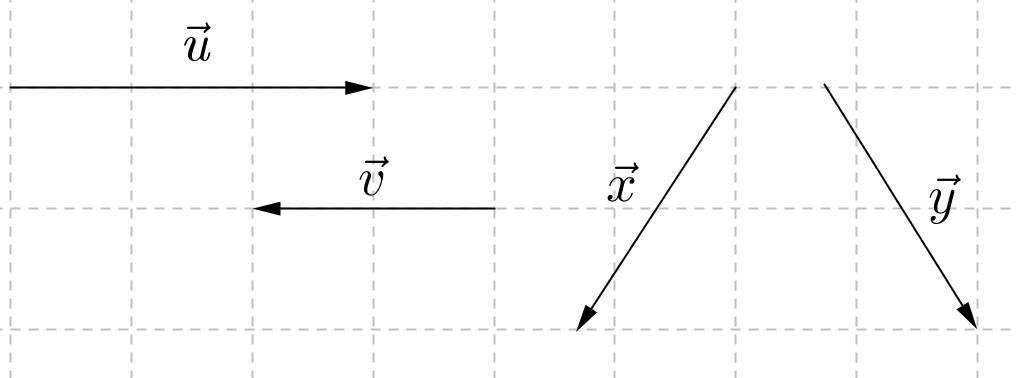
Mệnh đề nào dưới đây là đúng?

A. Hai vectơ $\overrightarrow{x}$ và $\overrightarrow{y}$ cùng hướng;

B. Hai vectơ $\overrightarrow{u}$ và $\overrightarrow{v}$ cùng hướng;

C. Hai vectơ $\overrightarrow{u}$ và $\overrightarrow{v}$ ngược hướng;

D. Hai vectơ $\overrightarrow{x}$ và $\overrightarrow{y}$ ngược hướng.

Câu 13: Vectơ có điểm đầu là A và điểm cuối là B được kí hiệu là:

A. AB;                 

B. BA;                 

C. $\overrightarrow{AB}$;

D. $\overrightarrow{BA}.$

Câu 14: Cho I là trung điểm của đoạn thẳng AB và M là một điểm tùy ý. Mệnh đề nào dưới đây đúng?

A. $\overrightarrow{MA}+\overrightarrow{MB}=\overrightarrow{IM}.$

B. $\overrightarrow{MA}+\overrightarrow{MB}=\overrightarrow{MI}.$

C. $\overrightarrow{MA}+\overrightarrow{MB}=2\overrightarrow{IM}.$

D. $\overrightarrow{MA}+\overrightarrow{MB}=2\overrightarrow{MI}.$

Câu 15: Cho hai tập hợp A = {1; 2; 3; 4; 5} và B = {1; 3; 5; 7}. Số phần tử của tập hợp A\B là

A. 2;                    

B. 3;                    

C. 1;                    

D. 6.

Câu 16: Cho hai tập hợp A = [– 2; 3), B = [1; 5]. Khi đó $A\cap B$ là tập hợp nào dưới đây ?

A. [– 2; 3);           

B. [1; 3);     

C. [1; 3];              

D. (– 2; 5).

Câu 17: Hàm số f(x) = x² đồng biến trên khoảng nào dưới đây ?

A. (0; +∞); 

B. (– 4; +∞);        

C. (– ∞; 0);           

D. (– ∞; – 1).

Câu 18: Cho hình chữ nhật ABCD có AB = 3a, BC = 4a. Độ dài của vectơ $\overrightarrow{AB}+\overrightarrow{AD}$ bằng

A. 25a;                

B. 7a;                   

C. 5a;                   

D. a.

Câu 19: Cặp số nào sau đây là nghiệm của bất phương trình – 3x + 5y ≤ 6.

A. (2; 8);

B. (– 10; – 3);

C. (3; 3);

D. (0; 2).

Câu 20: Cặp số nào sau đây không là nghiệm của hệ bất phương trình $\left\{\begin{array}{l}x+y\le 2\\ 2x-3y>-2\end{array}\right..$

A. (0; 0);

B. (1; 1);

C. (– 1; 1);

D. (– 1; – 1).

Câu 21: Cho 0° < α < 180°. Chọn câu trả lời đúng.

A. cosα < 0.

B. sinα > 0.

C. tanα < 0.

D. cotα > 0.

Câu 22: Miền nghiệm của bất phương trình x – 2y < 4 được xác định bởi miền nào (nửa mặt phẳng không bị gạch và không kể d) sau đây?

A.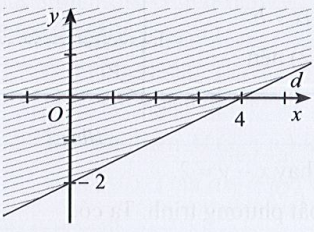 

B.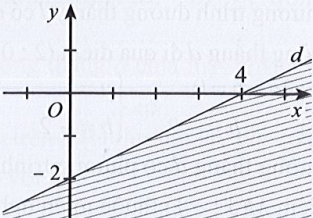

C.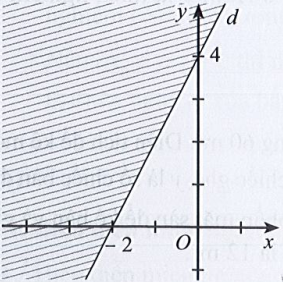 

D.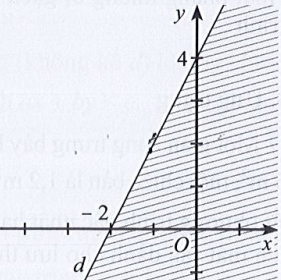 

Câu 23: Giá trị biểu thức T = sin²25° + sin²75° + sin²115° + sin²165° là:

A. T = sin 25°;

B. T = sin 75°;

C. T = 1;

D. T = 2.

Câu 24: Cho tam giác ABC có AB = 6,5 cm,  AC = 8,5 cm, $\widehat{A}=125°$. Tính độ dài cạnh BC (làm tròn kết quả đến hàng phần mười theo đơn vị tương ứng).

A. BC ≈ 177,9;

B. BC ≈ 13,3;

C. BC ≈ 51,1;

D. BC ≈ 7,1.

Câu 25: Miền nghiệm của bất phương trình 2x – 3y > 5 là nửa mặt phẳng (không kể đường thẳng d: 2x – 3y = 5) không chứa điểm có tọa độ nào sau đây?

A. (0; 0);

B. (3; 0);

C. (1; – 2);

D. (– 3; – 4).

II. PHẦN TỰ LUẬN

Câu 1: Giải tam giác ABC biết ABC có b = 14, c = 25 và $\widehat{A}$ = 120°.

Câu 2: Để lắp đường dây điện cao thế từ vị trí A đến vị trí B, do phải tránh một ngọn núi nên người ta phải nối đường dây từ vị trí A đến vị trí C dài 20 km, sau đó nối đường dây từ vị trí C đến vị trí B dài 12km. Góc tạo bởi dây AC và CB là 75°. Tính chiều dài tăng thêm vì không thể nối trực tiếp từ A đến B.

Câu 3: Anh Trung có kế hoạch đầu tư 400 triệu đồng vào hai khoản X và Y. Để đạt được lợi nhuận thì khoản X phải đầu tư ít nhất 100 triệu đồng và số tiền đầu tư cho khoản Y không nhỏ hơn số tiền cho khoản X. Viết hệ bất phương trình bậc nhất hai ẩn để mô tả hai khoản đầu tư đó và biểu diễn miền nghiệm của hệ bất phương trình vừa tìm được.

Câu 4: Lớp 10A có 36 học sinh, trong đó mỗi học sinh đều biết chơi ít nhất một trong hai môn thể thao đá cầu hoặc cầu lông. Biết rằng lớp 10A có 25 học sinh biết chơi đá cầu, có 20 học sinh biết chơi cầu lông. Hỏi lớp 10A có bao nhiêu học sinh biết chơi cả hai môn đá cầu và cầu lông?

Đáp án đề thi Toán 10 Giữa kì 1 Cánh diều - Đề số 01

I. PHẦN TRẮC NGHIỆM

1. A	2. B	3. C	4. C	5. A	6. A	7. B	8. A	9. C	10. D
11. A	12. C	13. C	14. D	15. B	16. B	17. D	18. C	19. C	20. C
21. B	22. B	23. D	24. B	25. B

Câu 1: Trong các câu dưới đây, câu nào là mệnh đề ?

A. Hà Nội là thủ đô của Việt Nam.              

B. Hôm nay là thứ mấy ?

C. Mệt quá !                                      

D. Mấy giờ rồi ?

Hướng dẫn giải

Đáp án đúng là: A

Ta có:

Câu “Hà Nội là thủ đô của Việt Nam” là câu khẳng định đúng. Do đó A là một mệnh đề.

Các câu “Hôm nay là thứ mấy?”, “Mấy giờ rồi?” là câu nghi vấn, không xác định được tính đúng sai. Do đó B và D không là mệnh đề.

Câu “Mệt quá!” là câu cảm thán không xác định được tính đúng sai. Do đó C không là mệnh đề.

Câu 2: Trong các mệnh đề dưới đây, mệnh đề nào đúng ?

A. 5 là số tự nhiên chẵn;          

B. 5 là số nguyên tố;

C. 5 là số nguyên âm;                                 

D. 5 là số chia hết cho 3.

Hướng dẫn giải

Đáp án đúng là: B

Ta có:

5 là số tự nhiên lẻ. Do đó A sai

5 có hai ước là 1 và chính nó nên 5 là số nguyên tố. Do đó B đúng.

5 là số nguyên dương. Do đó C sai.

5 chia 3 dư 2. Do đó D sai.

Câu 3: Cho tập hợp A = {1; 3; 5; 7; 9}. Số phần tử của tập hợp A là

A. 6;                    

B. 4;                    

C. 5;                    

D. 3.

Hướng dẫn giải

Đáp án đúng là: C

Tập hợp A có 5 phần tử.

Câu 4: Cho tập hợp $B=\left\{\left.x\in ℝ\right|a\le x<b\right\}.$ Mệnh đề nào dưới đây đúng ?

A. B = [a; b];        

B. B = (a; b];        

C. B = [a; b) ;        

D. B = (a; b).

Hướng dẫn giải

Đáp án đúng là: C

Ta có: $B=\left\{\left.x\in ℝ\right|a\le x<b\right\}=\left[a;b\right)$.

Câu 5: Tập xác định của hàm số $f\left(x\right)=\sqrt{x-2}$ là

A. D = [2; +∞);    

B. D = (2; +∞);    

C. D = (– ∞; 2);    

D. D = (– ∞; 2].

Hướng dẫn giải

Đáp án đúng là: A

Điều kiện xác định của hàm số f(x) là x – 2 ≥ 0 ⇔ x ≥ 2.

Vì vậy tập xác định của hàm số đã cho là D = [2; +∞).

Câu 6: Trong mặt phẳng Oxy, điểm nào dưới đây thuộc đồ thị của hàm số $y=\sqrt{x}?$

A. P(4; 2);  

B. M(1; – 1);        

C. N(2; 4);           

D. Q(2; – 4).

Hướng dẫn giải

Đáp án đúng là: A

Thay tọa độ điểm P(4; 2) với x = 4 và y = 2 vào hàm số, ta được: $2=\sqrt{4}$ là một mệnh đề đúng. Do đó P thuộc đồ thị hàm số đã cho.

Thay tọa độ điểm M(1; – 1) với x = 1 và y = – 1 vào hàm số, ta được: $-1=\sqrt{1}$ là một mệnh đề sai. Do đó M không thuộc đồ thị hàm số đã cho.

Thay tọa độ điểm N(2; 4) với x = 2 và y = 4 vào hàm số, ta được: $4=\sqrt{2}$ là một mệnh đề sai. Do đó N không thuộc đồ thị hàm số đã cho.

Thay tọa độ điểm Q(2; – 4) với x = 2 và y = – 4 vào hàm số, ta được: $-4=\sqrt{2}$ là một mệnh đề sai. Do đó Q không thuộc đồ thị hàm số đã cho.

Câu 7: Cho hàm số f(x) = x³ – 2. Giá trị f(1) bằng bao nhiêu?

A. 3;           

B. – 1;                  

C. 2; 

D. 1.

Hướng dẫn giải

Đáp án đúng là: B

Ta có: f(1) = 1³ – 2 = – 1.

Câu 8: Hàm số nào dưới đây có đồ thị là đường thẳng như trong hình bên ?

A. y = x + 1;

B. y = x – 1;

C. y = – x + 1;

D. y = – x – 1.

Hướng dẫn giải

Đáp án đúng là: A

Vì đồ thị hàm số là đường thẳng nên là hàm số bậc nhất và có dạng y = ax + b (a ≠ 0).

Theo quan sát, ta thấy hàm số đi qua hai điểm có tọa độ (0 ; 1) và (– 1; 0) ta có hệ phương trình:

$\left\{\begin{array}{l}-a+b=0\\ b=1\end{array}\right.\iff \left\{\begin{array}{l}a=1\\ b=1\end{array}\right.$

Vì vậy hàm số cần tìm là y = x + 1.

Câu 9: Trong các mệnh đề dưới đây, mệnh đề nào đúng ?

A. Hàm số y = x là hàm số nghịch biến trên ℝ.

B. Đồ thị hàm số y = x là một đường cong.

C. Hàm số y = x là hàm số đồng biến trên ℝ.

D. Hàm số y = x là hàm hằng.

Hướng dẫn giải

Đáp án đúng là: C

Hàm số y = x là đường thẳng và có a = 1 > 0 nên hàm số đồng biến trên ℝ. Do đó C đúng.

Câu 10: Trong mặt phẳng Oxy, biết điểm M(2; y₀) thuộc đồ thị của hàm số y = 2x – 3. Giá trị của y₀ bằng:

A. 2;                    

B. 0;                    

C. – 1;        

D. 1.

Hướng dẫn giải

Đáp án đúng là: D

Thay tọa độ điểm M với x = 2 và y = y₀ vào hàm số y = 2x – 3, ta được:

y₀ = 2.2 – 3 = 1.

Vậy y₀ = 1.

Câu 11: Trong mặt phẳng Oxy đồ thị của hàm số y = x² – 2x + 3 có trục đối xứng là đường thẳng nào dưới đây ?

A. x = 1;              

B. x = – 1;            

C. x = 2;               

D. x = – 2.

Hướng dẫn giải

Đáp án đúng là: A

Đồ thị hàm số y = x² – 2x + 3 là hàm số bậc hai có trục đối xứng là

x = $-\frac{b}{2a}=-\frac{-2}{2.1}=1$.

Câu 12: Cho các vectơ $\overrightarrow{u},\overrightarrow{v},\overrightarrow{x},\overrightarrow{y}$ như trong hình:

Mệnh đề nào dưới đây là đúng?

A. Hai vectơ $\overrightarrow{x}$ và $\overrightarrow{y}$ cùng hướng;

B. Hai vectơ $\overrightarrow{u}$ và $\overrightarrow{v}$ cùng hướng;

C. Hai vectơ $\overrightarrow{u}$ và $\overrightarrow{v}$ ngược hướng;

D. Hai vectơ $\overrightarrow{x}$ và $\overrightarrow{y}$ ngược hướng.

Hướng dẫn giải

Đáp án đúng là: C

Từ hình vẽ, ta có:

Hai vectơ $\overrightarrow{u}$ và $\overrightarrow{v}$có giá là hai đường thẳng song song nên $\overrightarrow{u}$ và $\overrightarrow{v}$cùng phương. Vectơ  $\overrightarrow{u}$ có hướng từ trái sáng phải còn vectơ $\overrightarrow{v}$có hướng từ phải sang trái. Do đó hai vectơ này ngược hướng.

Hai vectơ $\overrightarrow{x}$ và $\overrightarrow{y}$có giá là hai đường thẳng không song song nên $\overrightarrow{x}$ và $\overrightarrow{y}$ không cùng phương. Do đó hai vectơ này không cùng hướng cũng không ngược hướng.

Câu 13: Vectơ có điểm đầu là A và điểm cuối là B được kí hiệu là:

A. AB;                 

B. BA;                 

C. $\overrightarrow{AB}$;

D. $\overrightarrow{BA}.$

 

Hướng dẫn giải

Đáp án đúng là: C

Vectơ có điểm đầu là A và điểm cuối là B được kí hiệu là: $\overrightarrow{AB}$.

Câu 14: Cho I là trung điểm của đoạn thẳng AB và M là một điểm tùy ý. Mệnh đề nào dưới đây đúng?

A. $\overrightarrow{MA}+\overrightarrow{MB}=\overrightarrow{IM}.$

B. $\overrightarrow{MA}+\overrightarrow{MB}=\overrightarrow{MI}.$

C. $\overrightarrow{MA}+\overrightarrow{MB}=2\overrightarrow{IM}.$

D. $\overrightarrow{MA}+\overrightarrow{MB}=2\overrightarrow{MI}.$

Hướng dẫn giải

Đáp án đúng là: D

Câu 15: Cho hai tập hợp A = {1; 2; 3; 4; 5} và B = {1; 3; 5; 7}. Số phần tử của tập hợp A\B là

A. 1;                    

B. 2;                    

C. 3;                    

D. 6.

Hướng dẫn giải

Đáp án đúng là: B

Ta có: A\B = {2; 4}.

Do đó tập hợp này có 2 phần tử.

Câu 16: Cho hai tập hợp A = [– 2; 3), B = [1; 5]. Khi đó $A\cap B$ là tập hợp nào dưới đây ?

A. [– 2; 3);           

B. [1; 3);     

C. [1; 3];              

D. (– 2; 5).

Hướng dẫn giải

Đáp án đúng là: B

Ta có hình vẽ sau:

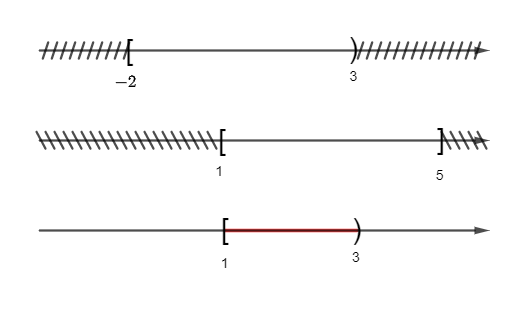
Khi đó  = [1; 3).

Câu 17: Hàm số f(x) = x² đồng biến trên khoảng nào dưới đây ?

A. (– ∞; – 1);

B. (– 4; +∞);        

C. (– ∞; 0);           

D. (0; +∞).

Hướng dẫn giải

Đáp án đúng là: D

Xét hàm số bậc hai y = x² có:

Tọa độ điểm đỉnh là x = $-\frac{b}{2a}=-\frac{0}{2.1}=0\Rightarrow y=0$.

Ta có a = 1 > 0, khi đó:

Hàm số đồng biến trên (0; +∞);

Hàm số nghịch biến trên (– ∞; 0).

Câu 18: Cho hình chữ nhật ABCD có AB = 3a, BC = 4a. Độ dài của vectơ $\overrightarrow{AB}+\overrightarrow{AD}$ bằng

A. 25a;                

B. 7a;                   

C. 5a;                   

D. a.

Hướng dẫn giải

Đáp án đúng là: C

Xét tam giác ABC vuông tại B, ta có:

AC² = AB² + BC² = (3a)² + (4a)² = 25a² (định lí Py – ta – go)

⇒ AC = 5a.

Vì ABCD là hình chữ nhật nên ABCD là hình bình hành. Do đó: $\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}$

⇒ $\left|\overrightarrow{AB}+\overrightarrow{AD}\right|=\left|\overrightarrow{AC}\right|=AC=5a.$

Câu 19: Cặp số nào sau đây là nghiệm của bất phương trình – 3x + 5y ≤ 6.

A. (2; 8);

B. (– 10; – 3);

C. (3; 3);

D. (0; 2).

Hướng dẫn giải

Đáp án đúng là C

+) Thay x = 2, y = 8 vào bất phương trình – 3x + 5y ≤ 6, ta được:

– 3.2 + 5.8 ≤ 6 ⇔ 34 ≤ 6 (vô lí)

Do đó cặp số (2; 8) không là nghiệm của bất phương trình đã cho.

+) Thay x = – 10, y = – 3 vào bất phương trình – 3x + 5y ≤ 6, ta được:

– 3.(–10) + 5.(–3) ≤ 6 ⇔ 15 ≤ 6 (vô lí)

Do đó cặp số (– 10; – 3) không là nghiệm của bất phương trình đã cho.

+) Thay x = 3, y = 3 vào bất phương trình – 3x + 5y ≤ 6, ta được:

– 3.3 + 5.3 ≤ 6 ⇔ 6 ≤ 6 (luôn đúng)

Do đó cặp số (3; 3) không là nghiệm của bất phương trình đã cho.

+) Thay x = 0, y = 2 vào bất phương trình – 3x + 5y ≤ 6, ta được:

– 3.0 + 5.2 ≤ 6 ⇔ 10 ≤ 6 (vô lí)

Do đó cặp số (0; 2) không là nghiệm của bất phương trình đã cho.

Câu 20: Cặp số nào sau đây không là nghiệm của hệ bất phương trình $\left\{\begin{array}{l}x+y\le 2\\ 2x-3y>-2\end{array}\right..$

A. (0; 0);

B. (1; 1);

C. (– 1; 1);

D. (– 1; – 1).

Hướng dẫn giải

Đáp án đúng là C

Xét hệ phương trình: $\left\{\begin{array}{l}x+y\le 2\left(1\right)\\ 2x-3y>-2\left(2\right)\end{array}\right..$

+) Thay x = 0 và y = 0 lần lượt vào các bất phương trình (1) và (2) trong hệ, ta được:

(1) ⇔ 0 + 0 ≤ 2 ⇔ 0 ≤ 2 (luôn đúng);

(2) ⇔ 2.0 – 3.0 > – 2 ⇔ 0 > – 2 (luôn đúng).

Do đó cặp số (0; 0) là nghiệm của hệ bất phương trình đã cho.

+) Thay x = 1 và y = 1 lần lượt vào các bất phương trình (1) và (2) trong hệ, ta được:

(1) ⇔ 1 + 1 ≤ 2 ⇔ 2 ≤ 2 (luôn đúng);

(2) ⇔ 2.1 – 3.1 > – 2 ⇔ – 1 > – 2 (luôn đúng).

Do đó cặp số (1; 1) là nghiệm của hệ bất phương trình đã cho.

+) Thay x = – 1 và y = 1 lần lượt vào các bất phương trình (1) và (2) trong hệ, ta được:

(1) ⇔ – 1 + 1 ≤ 2 ⇔ 0 ≤ 2 (luôn đúng);

(2) ⇔ 2.(– 1) – 3.1 > – 2 ⇔ – 5 > – 2 (vô lí).

Do đó cặp số (– 1; 1) không là nghiệm của hệ bất phương trình đã cho.

+) Thay x = – 1 và y = – 1 lần lượt vào các bất phương trình (1) và (2) trong hệ, ta được:

(1) ⇔ – 1 + (– 1) ≤ 2 ⇔ – 2 ≤ 2 (luôn đúng);

(2) ⇔ 2.(– 1) – 3.(– 1) > – 2 ⇔ 1 > – 2 (luôn đúng).

Do đó cặp số (– 1; – 1) là nghiệm của hệ bất phương trình đã cho.

Vậy cặp số (– 1; 1) không là nghiệm của hệ bất phương trình đã cho.

Câu 21: Cho 0° < α < 180°. Chọn câu trả lời đúng.

A. cosα < 0.

B. sinα > 0.

C. tanα < 0.

D. cotα > 0.

Hướng dẫn giải

Đáp án đúng là B

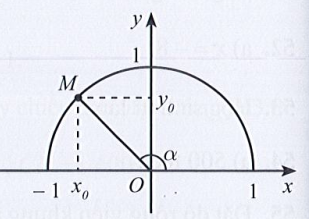
Với 0° < α < 180°, ta có:

– 1 < cosα < 1. Suy ra A sai.

0 < sinα < 1. Suy ra B đúng.

Do đó C và D sai.

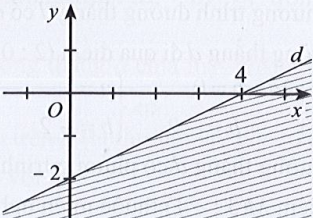
Câu 22: Miền nghiệm của bất phương trình x – 2y < 4 được xác định bởi miền nào (nửa mặt phẳng không bị gạch và không kể d) sau đây?

A. 

B.

C. 

D. 

Hướng dẫn giải

Đáp án đúng là B

Phương trình đường thẳng d có dạng: x – 2y = 4.

Đường thẳng d cắt hai trục tọa độ Ox, Oy lần lượt tại hai điểm có tọa độ (4; 0) và (0; – 2).

Ta có: 0 – 2.0 = 0 < 4 (luôn đúng). Do đó miền nghiệm của bất phương trình chứa điểm (0; 0) và không chứa đường thẳng d.

Khi đó miền nghiệm là nửa mặt phẳng không bị gạch và không kể d được thể hiện trong hình vẽ sau:

Câu 23: Giá trị biểu thức T = sin²25° + sin²75° + sin²115° + sin²165° là:

A. T = sin 25°;

B. T = sin 75°;

C. T = 1;

D. T = 2.

Hướng dẫn giải

Đáp án đúng là D

T = sin²25° + sin²75° + sin²115° + sin²165°

= sin²25° + sin²75° + sin²75° + sin²25°

= 2sin²25° + 2sin²75°

= 2sin²25° + 2cos²25°

= 2(sin²25° + cos²25°)

= 2.1 = 2.

Câu 24: Cho tam giác ABC có AB = 6,5 cm,  AC = 8,5 cm, $\widehat{A}=125°$. Tính độ dài cạnh BC (làm tròn kết quả đến hàng phần mười theo đơn vị tương ứng).

A. BC ≈ 177,9;

B. BC ≈ 13,3;

C. BC ≈ 51,1;

D. BC ≈ 7,1.

Hướng dẫn giải

Đáp án đúng là: B

Xét tam giác ABC, có:

BC² = AB² + AC² – 2.AB.AC.cosA

⇔ BC² = 6,5² + 8,5² – 2.6,5.8,5.cos125°

⇔ BC² ≈ 177,9

⇔ BC ≈ 13,3.

 Vậy BC ≈ 13,3.

Câu 25: Miền nghiệm của bất phương trình 2x – 3y > 5 là nửa mặt phẳng (không kể đường thẳng d: 2x – 3y = 5) không chứa điểm có tọa độ nào sau đây?

A. (0; 0);

B. (3; 0);

C. (1; – 2);

D. (– 3; – 4).

Hướng dẫn giải

Đáp án đúng là B

+) Thay x = 0, y = 0 vào bất phương trình 2x – 3y > 5, ta được:

2.0 – 3.0 > 5 ⇔ 0 > 5 (vô lí)

Do đó cặp số (0; 0) không thuộc miền nghiệm của bất phương trình đã cho.

+) Thay x = 3, y = 0 vào bất phương trình 2x – 3y > 5, ta được:

2.3 – 3.0 > 5 ⇔ 6 > 5 (thỏa mãn)

Do đó cặp số (0; 0) thuộc miền nghiệm của bất phương trình đã cho.

+) Thay x = 1, y = – 2 vào bất phương trình 2x – 3y > 5, ta được:

2.1 – 3.(– 2)  > 5 ⇔ 8 > 5 (thỏa mãn)

Do đó cặp số (1; – 2) thuộc miền nghiệm của bất phương trình đã cho.

+) Thay x = – 3, y = –4 vào bất phương trình 2x – 3y > 5, ta được:

2.(– 3) – 3.(– 4)  > 5 ⇔ 6 > 5 (thỏa mãn)

Do đó cặp số (– 3; – 4) thuộc miền nghiệm của bất phương trình đã cho.

II. PHẦN TỰ LUẬN

Câu 1: Giải tam giác ABC biết ABC có b = 14, c = 25 và $\widehat{A}$ = 120°.

Lời giải

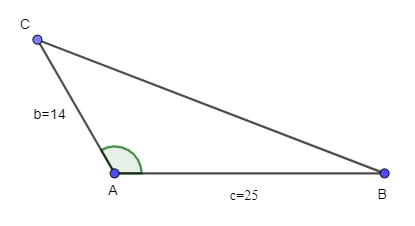
Xét ∆ABC, có:

Áp dụng định lí cosin, ta có:

BC² = AB² + AC² – 2AB.AC.cosA

⇔ BC² = 25² + 14² – 2.25.14.cos120°

⇔ BC² = 1 171

⇔ BC ≈ 34,22.

Áp dụng hệ quả của định lí cosin, ta có:

cosB = $\frac{a^2+c^2-b^2}{2.a.c}\approx \frac{34,{22}^2+{25}^2-{14}^2}{2.34,22.25}\approx 0,94$ ⇒ $\widehat{B}\approx 20°45\text{'}$.

Ta có: $\widehat{C}=180°-\widehat{A}-\widehat{B}\approx 180°-120°-20°45\text{'}=39°15\text{'}$.

Câu 2: Để lắp đường dây điện cao thế từ vị trí A đến vị trí B, do phải tránh một ngọn núi nên người ta phải nối đường dây từ vị trí A đến vị trí C dài 20 km, sau đó nối đường dây từ vị trí C đến vị trí B dài 12km. Góc tạo bởi dây AC và CB là 75°. Tính chiều dài tăng thêm vì không thể nối trực tiếp từ A đến B.

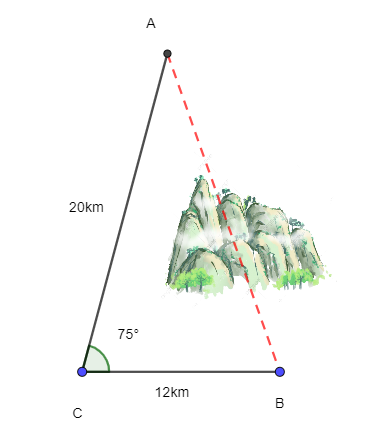
Lời giải

Xét tam giác ABC, có:

Áp dụng định lí cosin trong tam giác ABC, có:

AB² = BC² + AC² – 2.AB.BC.cosA

⇔ AB² = 12² + 20² – 2.12.20.cos75°

⇔ AB² ≈ 419,77

⇔ AB ≈ 20,49 (km).

Ta có: AC + BC = 20 + 12 = 32 (km).

Vậy chiều dài tăng thêm vì không thể nối trực tiếp từ A đến B là 32 – 20,49 ≈ 11,51 km.

Câu 3: Anh Trung có kế hoạch đầu tư 400 triệu đồng vào hai khoản X và Y. Để đạt được lợi nhuận thì khoản X phải đầu tư ít nhất 100 triệu đồng và số tiền đầu tư cho khoản Y không nhỏ hơn số tiền cho khoản X. Viết hệ bất phương trình bậc nhất hai ẩn để mô tả hai khoản đầu tư đó và biểu diễn miền nghiệm của hệ bất phương trình vừa tìm được.

Lời giải

Gọi x (triệu đồng) là số tiền anh Trung đầu tư vào khoản X và y (triệu đồng) là số tiền anh Trung đầu tư vào khoản Y (x, y ≥ 0).

Vì anh Trung đầu tư 400 triệu đồng vào hai khoản X và Y nên ta có x + y ≤ 400.

Để đạt được lợi nhuận thì khoản X phải đầu tư ít nhất 100 triệu đồng nên ta có x ≥ 100 và số tiền đầu tư cho khoản Y không nhỏ hơn số tiền cho X nên ta cũng có y ≥ x hay x – y ≤ 0.

Từ đó ta có hệ bất phương trình sau: $\left\{\begin{array}{l}x+y\le 400\\ x\ge 100\\ x-y\le 0\end{array}\right.$.

Ta vẽ bốn đường thẳng:

d₁: x + y = 400 là đường thẳng đi qua hai điểm có tọa độ (400; 0) và (0; 400);

d₂: x = 100 là đường thẳng song song với trục Oy và đi qua điểm có tọa độ (100; 0);

d₃: x – y = 0 là đường thẳng đi qua hai điểm có tọa độ (0; 0) và (1; 1).

Ta xác định từng miền nghiệm của từng bất phương trình trong hệ, gạch đi các phần không thuộc miền nghiệm của mỗi bất phương trình.

Miền nghiệm của hệ bất phương trình là miền trong tứ giác ABCD với  như hình vẽ sau:

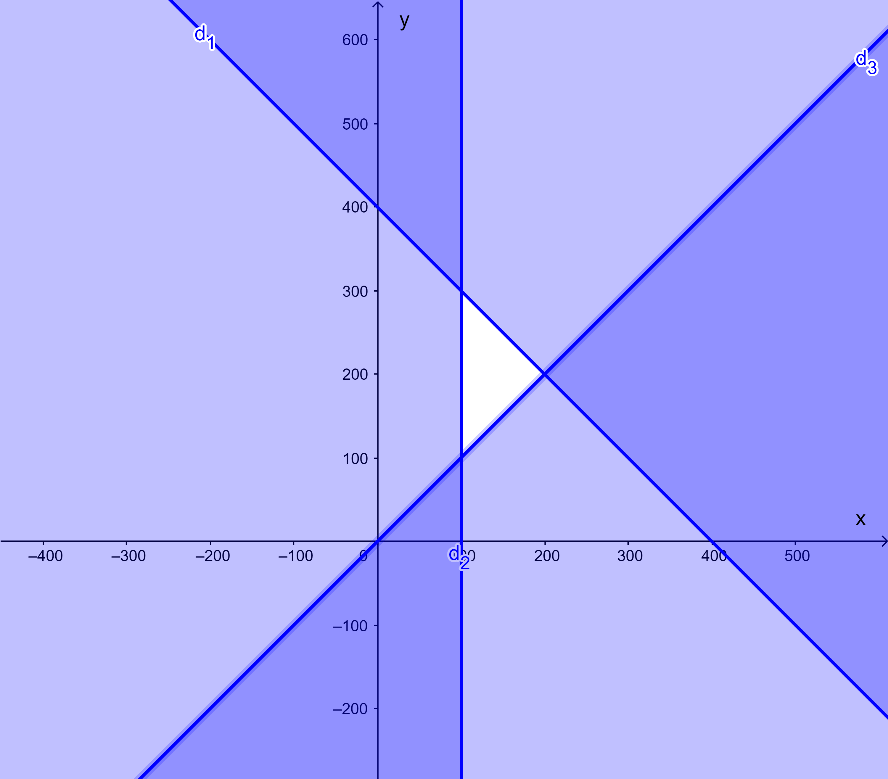
Câu 4: Lớp 10A có 36 học sinh, trong đó mỗi học sinh đều biết chơi ít nhất một trong hai môn thể thao đá cầu hoặc cầu lông. Biết rằng lớp 10A có 25 học sinh biết chơi đá cầu, có 20 học sinh biết chơi cầu lông. Hỏi lớp 10A có bao nhiêu học sinh biết chơi cả hai môn đá cầu và cầu lông?

Lời giải

Gọi A là tập hợp số học sinh biết chơi đá cầu. Khi đó |A| = 25;

B là tập hợp số học sinh biết chơi cầu lông. Khi đó |B| = 20.

Vì mỗi học sinh đều biết chơi ít nhất một trong hai môn thể thao đá cầu hoặc cầu lông nên ta có: A ∪ B là tập hợp số học sinh của lớp 10A. Khi đó |A ∪ B| = 36.

Ta có: |A ∪ B| = |A| + |B| – |A ∩ B| ⇒ |A ∩ B| = 25 + 20 – 36 = 9 (học sinh).

Vậy lớp 10A có 9 học sinh biết chơi cả hai môn đá cầu và cầu lông.

B. MA TRẬN ĐỀ THI GIỮA KỲ 1 TOÁN 10 Cánh diều (Có đáp án)- ĐỀ SỐ 02

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Giữa Học kì 1

Năm học 2022 - 2023

Môn: Toán 10

Thời gian làm bài: 90 phút

Đề thi Giữa kì 1 Toán 10 Cánh diều (Có đáp án) - Đề số 02

I. PHẦN TRẮC NGHIỆM

Câu 1. Cho tập hợp A và a là một phần tử của tập hợp A. Trong các mệnh đề sau, mệnh đề nào sai?

A. {a} ⊂ A;                

B. {a} ∈ A;                

C. a ∈ A;                    

D. $\varnothing \subset A$.

Câu 2. Cho mệnh đề chứa biến  P(n): “n² chia hết cho 4 ” với n là số nguyên. Chọn mệnh đề đúng trong các mệnh đề sau:

A. P(5);                      

B. P(2);                       

C. P(4);                       

D. P(6).   

Câu 3. Mệnh đề phủ định của mệnh đề “Phương trình ax² + bx + c = 0 (a ≠ 0) vô nghiệm” là:

A. Phương trình ax² + bx + c = 0 (a ≠ 0)  không có nghiệm;

B. Phương trình ax² + bx + c = 0 (a ≠ 0)  có nghiệm;

C. Phương trình ax² + bx + c = 0 (a ≠ 0)  có 2 nghiệm phân biệt;

D. Phương trình ax² + bx + c = 0 (a ≠ 0)  có nghiệm kép.

Câu 4. Gọi A là tập hợp các số thực không nhỏ hơn 1 và B là tập hợp các số thực có giá trị tuyệt đối nhỏ hơn 2. Tìm$A\cap B$

A. $A\cap B=(1;2)$;

B. $A\cap B=[1;2)$;

C. $A\cap B=[1;2]$;

D. $A\cap B=(-2;1)$.

Câu 5. Cho A = {0; 1; 2; 3; 4} và B = {2; 3; 4; 5; 6}. Tập hợp (A \ B) ∪ (B \ A) bằng?

A. {5; 6};

B.  {2; 3; 4};

C. {1; 2};

D. {0; 1; 5; 6}.

Câu 6: Số phần tử của tập hợp A = {k² + 1| k ∈ ℤ, |k| ≤ 2} bằng

A. 1;

B. 5;

C. 3;

D. 2.

Câu 7: Cho hai tập hợp (1; 3) và [2; 4]. Giao của hai tập hợp đã cho là

A. (2; 3];                             

B. (2; 3);                             

C. [2; 3);                             

D. [2; 3].

Câu 8: Hình vẽ sau đây (phần không bị gạch) là biểu diễn của tập hợp nào?

A. (– ∞; – 2) ∪ [5; +∞);    

B. (– ∞; – 2) ∪ (5; +∞);    

C. (– ∞; – 2] ∪ (5; +∞);

D. (– ∞; – 2] ∪ [5; +∞).

Câu 9. Lớp 10A₁ có 6 học sinh giỏi Toán, 4 học sinh giỏi Lý, 5 học sinh giỏi Hóa, 2 học sinh giỏi Toán và Lý, 3 học sinh giỏi Toán và Hóa, 2 học sinh giỏi Lý và Hóa, 1 học sinh giỏi cả 3 môn Toán, Lý, Hóa. Số học sinh giỏi ít nhất một môn (Toán, Lý, Hóa) của lớp 10A₁ là:

A. 15;                                  

B. 23;                                  

C. 7;                                    

D. 9.

Câu 10. Cặp số (x; y) nào sau đây là nghiệm của bất phương trình 5x – 3y ≤ 2?

A.  (0; – 2);                

B.  (3; 0);                    

C.  (2; 1);                    

D.  (– 1; – 1).

Câu 11. Bất phương trình nào sau đây không là bất phương trình bậc nhất một ẩn?

A. 8 – $\sqrt{2}$x ≤ 0; 

B. 4x – 3 > 0;    

C. $\frac{1}{3}$x – 3 < 0;

D.  (x + 1)² ≥ 1.

Câu 12. Phần mặt phẳng không bị gạch chéo trong hình vẽ bên (kể cả biên) là biểu diễn hình học tập nghiệm của hệ bất phương trình nào dưới đây?

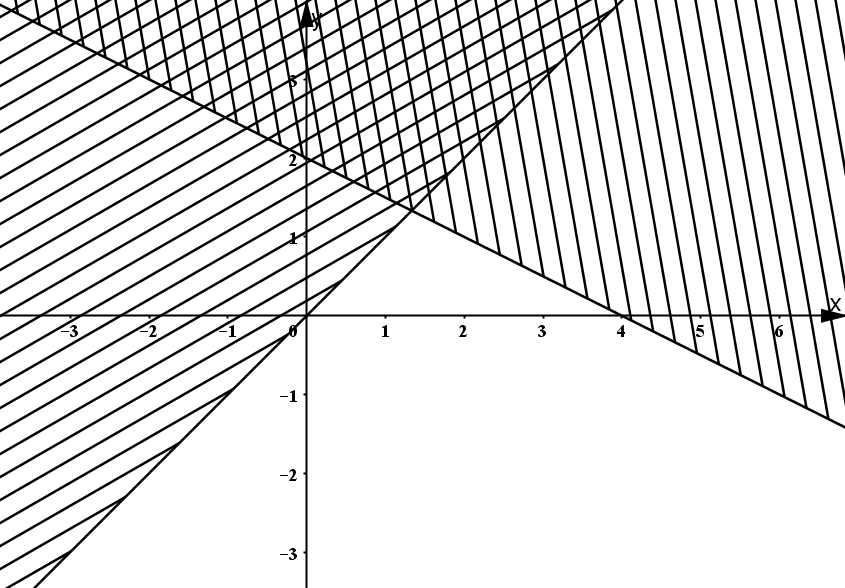
A. $\left\{\begin{array}{l}x-y\ge 0\\ x+2y\le 4\end{array}\right.$;           

B. $\left\{\begin{array}{l}x-y\le 0\\ x+2y\ge 4\end{array}\right.$;

C. $\left\{\begin{array}{l}x-y\ge 0\\ x+2y\ge 4\end{array}\right.$ 

D. $\left\{\begin{array}{l}x-y\le 0\\ x+2y\le 4\end{array}\right.$.

Câu 13. Cho sin35° ≈ 0,57. Giá trị của sin145° gần với giá trị nào nhất sau đây:

A. 0,57;    

B. 1;

C. $\frac{\sqrt{2}}{2}$;

D. 0,15.

Câu 14. Tính giá trị biểu thức: A = cos 0° + cos 40° + cos 120° + cos 140°

A. $\frac{1}{2}$;        

B. – 0,5;   

C. 1;

D. 0.

Câu 15. Cho tam giác ABC, ta có các đẳng thức:

(I) sin$\frac{A}{2}$ = sin$\frac{B+C}{2}$;

(II) tan$\frac{A}{2}$ = cot$\frac{B+C}{2}$;

(III) sinA = sin(B + C).

Có bao nhiêu đẳng thức đúng?

A. $\frac{1}{2}$;        

B. – 0,5;   

C. 1;

D. 0.

Câu 16. Cho điểm M(x₀; y₀) nằm trên đường tròn đơn vị thỏa mãn $\widehat{xOM}=\alpha$. Khi đó phát biểu nào dưới đây là sai?

A. sinα = x₀;      

B. cosα = x₀;      

C. tanα = $\frac{y_0}{x_0}$;

D. cotα = $\frac{x_0}{y_0}$.

Câu 17. Trong các công thức dưới đây, công thức nào sai về cách tính diện tích tam giác ABC? Biết AB = c, AC = b, BC = a, h_a, h_b, h_c lần lượt là các đường cao kẻ từ đỉnh A, B, C, r là bán kính đường tròn nội tiếp, R là bán kính đường tròn ngoại tiếp tam giác ABC.

A. S_ABC = pr;     

B. S_ABC = $\frac{1}{2}$c.a.sinA;

C. S_ABC = $\sqrt{p(p-a)(p-b)(p-c)}$;

D. S_ABC = $\frac{abc}{4R}$.

Câu 18. Cho tam giác ABC, có các cạnh AB = c, AC = b, BC = a. Định lí sin được phát biểu:

A. $\frac{a}{\text{cos}A}=\frac{b}{\cos B}=\frac{c}{\cos C}$;       

B. $\frac{a}{\text{sin}A}=\frac{b}{\sin B}=\frac{c}{\sin C}$;         

C. a.cosA = b.cosB = c.cosC;

D. a.sinA = b.sinB = c.sinC.

Câu 19. Cho tam giác ABC có BC = 50 cm, $\widehat{B}=65°,\widehat{C}=45°$. Tính (làm tròn kết quả đến hàng phần mười theo đơn vị xăng – ti – mét). Chu vi của tam giác ABC là:

A. 135,84;

B. 67,92;  

C. 131,91;

D. 65,96.

Câu 20. Một người đứng ở vị trí A trên nóc một ngôi nhà cao 8m đang quan sát một cây cao cách ngôi nhà 25m và đo được $\widehat{BAC}=65°$. Chiều cao của cây gần với kết quả nào nhất sau đây?

A. 38m;    

B. 39m;    

C. 19m;

D. 20m.

Câu 21. Đẳng thức nào sau đây, mô tả đúng hình vẽ bên?

A. $3\overrightarrow{AI}+\overrightarrow{AB}=\overrightarrow{0}$.

B. $\overrightarrow{BI}+3\overrightarrow{BA}=\overrightarrow{0}$.

C. $3\overrightarrow{IA}+\overrightarrow{IB}=\overrightarrow{0}$. 

D. $\overrightarrow{AI}+3\overrightarrow{AB}=\overrightarrow{0}$.

Câu 22: Cho hình chữ nhật ABCD. Hãy chọn khẳng định đúng.

A. $\overrightarrow{AB}=\overrightarrow{AD}$.                       

B. $\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}$.               

C. $\left|\overrightarrow{AB}\right|=\left|\overrightarrow{AD}\right|$.                     

D. $\overrightarrow{AB}=\overrightarrow{CD}$.

Câu 23. Cho hình bình hành ABCD với điểm K thỏa mãn $\overrightarrow{KA}+\overrightarrow{KC}=\overrightarrow{AB}$ thì

A. K là trung điểm của AC.                       

B. K là trung điểm của AD.

C. K là trung điểm của AB.                        

D. K là trung điểm của BD.

Câu 24. Cho tam giác đều ABC có AB = a, M là trung điểm của BC. Khi đó $\left|\overrightarrow{MA}+\overrightarrow{AC}\right|$ bằng

A. $\frac{a}{4}$. 

B. 2a.   

C. $\frac{a}{2}$.   

D. a.

Câu 25. Cho hình bình hành ABCD. Mệnh đề nào sau đây đúng?

A. $\overrightarrow{AC}=\overrightarrow{BC}$.                

B. $\overrightarrow{AD}=\overrightarrow{CD}$.               

C. $\overrightarrow{AB}=\overrightarrow{DC}$.               

D. $\overrightarrow{AC}=\overrightarrow{BD}$.

Câu 26. Cho hình chữ nhật ABCD tâm O. Gọi M, N lần lượt là trung điểm của các cạnh AB, AD. Chọn khẳng định đúng trong các khẳng định sau:

A. $\overrightarrow{AB}=\overrightarrow{CD}$;                       

B. $\overrightarrow{AN}=\overrightarrow{MO}$;

C. $\overrightarrow{OC}=\overrightarrow{OD}$;                       

D. $\overrightarrow{AM}=\overrightarrow{BM}$.

Câu 27. Phát biểu nào sau đây là sai?

A. Độ dài của vectơ là khoảng cách giữa điểm đầu và điểm cuối của vectơ đó.

B. Vectơ là đoạn thẳng có hướng.

C. Hai vectơ cùng hướng thì cùng phương.

D. Hai vectơ cùng phương thì cùng hướng.

Câu 28. Cho hình thang MNPQ, MN // PQ, MN = 2PQ. Phát biểu nào dưới đây là đúng?

A. $\overrightarrow{MN}=2\overrightarrow{PQ}$;

B. $\overrightarrow{MQ}=2\overrightarrow{NP}$;                     

C. $\overrightarrow{MN}=-2\overrightarrow{PQ}$;                   

D. $\overrightarrow{MQ}=-2\overrightarrow{NP}$.

Câu 29. Cho tam giác đều ABC nội tiếp đường tròn tâm O bán kính bằng 1. Gọi M là điểm nằm trên đường tròn (O), độ dài vectơ $\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}$ bằng

A. 1;                                    

B. 6;                                    

C. $\sqrt{3}$;                                

D. 3.

Câu 30. Cho tam giác ABC đều có cạnh bằng a, gọi H là trung điểm của cạnh BC. Độ dài của vectơ $2\left(\overrightarrow{HA}-\overrightarrow{HC}\right)$bằng

A. a;                                    

B. 2a;                                  

C. $\frac{a\sqrt{3}}{2}$; 

D. $a\sqrt{3}$.

II. TỰ LUẬN

Bài 1 (1,0 điểm).

a) Cho tập hợp A = {x ∈ ℝ | x² = 2} và B = {x ∈ ℕ| x² + 5x – 6 = 0}. Tìm tập hợp A ∩ B và A ∪ B.

b) Cho tập hợp A = (m ; m + 2] và B = [– 1 ; 5]. Tìm m để A ⊂ B.

Bài 2 (1,5 điểm). Tìm giá trị nhỏ nhất của biểu thức F(x; y) = – 2x + y trên miền nghiệm của hệ bất phương trình $\left\{\begin{array}{l}x-y\ge -2\\ x+y\le 4\\ x-5y\le -2\end{array}\right.$.

Bài 3 (1,5 điểm).

a) Cho 4 điểm M,N, P, Q bất kỳ, chứng minh rằng $\overrightarrow{MP}+\overrightarrow{NQ}-\overrightarrow{NP}=\overrightarrow{MQ}$.

b) Cho hình bình hành ABCD. Gọi E là điểm thỏa mãn $4\overrightarrow{DE}=\overrightarrow{DC}$ và G là trọng tâm tam giác ABE. Đường thẳng AG cắt BC tại F.  Biểu diễn $\overrightarrow{AG}$ theo $\overrightarrow{AB}$, $\overrightarrow{AD}$ và tính tỉ số $\frac{BF}{BC}$.

Đáp án đề thi Giữa kì 1 Toán 10 Cánh diều - Đề số 02

I. PHẦN TRẮC NGHIỆM

1.B	2.C	3.B	4.B	5.D	6.C	7.C	8.D	9.D	10.D
11.D	12.A	13.A	14.A	15.C	16.A	17.B	18.B	19.B	20.A
21.A	22.B	23.B	24.C	25.C	26.B	27.D	28.C	29.D	30.B

Câu 1. Cho tập hợp A và a là một phần tử của tập hợp A. Trong các mệnh đề sau, mệnh đề nào sai?

A. {a} ⊂ A;                

B. {a} ∈ A;                

C. a ∈ A;                    

D. $\varnothing \subset A$.

Hướng dẫn giải

Đáp án đúng là: B

Ta có a là một phần tử của tập hợp A nên ta viết a ∈ A. Do đó C là mệnh đề đúng và B là mệnh đề sai.

Ta lại có {a} là tập con của tập A nên ta viết {a} ⊂ A. Do đó A là mệnh đề đúng.

Ngoài ra tập $\varnothing$ là tập con của tất cả các tập hợp nên ta có $\varnothing \subset A$. Do đó D là mệnh đề đúng.

Câu 2. Cho mệnh đề chứa biến  P(n): “n² chia hết cho 4 ” với n là số nguyên. Chọn mệnh đề đúng trong các mệnh đề sau:

A. P(5);                      

B. P(3);                       

C. P(2);                       

D. P(1).   

Hướng dẫn giải

Đáp án đúng là: C

Với n = 5 ta có mệnh đề P(5): “5² chia hết cho 4 ”. Đây là mệnh đề sai vì 5² = 25 chia cho 4 dư 1.

Với n = 3 ta có mệnh đề P(3): “3² chia hết cho 4 ”. Đây là mệnh đề sai vì 3² = 9 chia cho 4 dư 1.

Với n = 2 ta có mệnh đề P(2): “2² chia hết cho 4 ”. Đây là mệnh đề đúng vì 2² = 4 chia hết cho 4.

Với n = 1 ta có mệnh đề P(1): “1² chia hết cho 4 ”. Đây là mệnh đề sai vì 1² = 1 chia cho 4 dư 1.

Câu 3. Mệnh đề phủ định của mệnh đề “Phương trình ax² + bx + c = 0 (a ≠ 0) vô nghiệm” là:

A. Phương trình ax² + bx + c = 0 (a ≠ 0)  không có nghiệm;

B. Phương trình ax² + bx + c = 0 (a ≠ 0)  có nghiệm;

C. Phương trình ax² + bx + c = 0 (a ≠ 0)  có 2 nghiệm phân biệt;

D. Phương trình ax² + bx + c = 0 (a ≠ 0)  có nghiệm kép.

Hướng dẫn giải

Đáp án đúng là: B

Ta có mệnh đề phủ định của mệnh đề “Phương trình ax² + bx + c = 0 (a ≠ 0) vô nghiệm” là: Phương trình ax² + bx + c = 0 (a ≠ 0)  có nghiệm.

Câu 4. Gọi A là tập hợp các số thực không nhỏ hơn 1 và B là tập hợp các số thực có giá trị tuyệt đối nhỏ hơn 2. Tìm$A\cap B$

A. $A\cap B=(1;2)$;

B. $A\cap B=[1;2)$;

C. $A\cap B=[1;2]$;

D. $A\cap B=(-2;1)$.

Hướng dẫn giải

Đáp án đúng là: B

Ta có A là tập hợp các số thực không nhỏ hơn 1 nên bằng cách chỉ ra tính chất đặc trưng tập hợp A được viết thành: A = {x ∈ ℝ| x ≥ 1} = [1; +∞).

Ta lại có B là tập hợp các số thực có giá trị tuyệt đối nhỏ hơn 2 nên bằng cách chỉ ra tính chất đặc trưng tập hợp B được viết thành: B = {x ∈ ℝ| |x| < 2} = {x ∈ ℝ| x < 2 hoặc x > – 2} = (– 2; 2).

Biểu diễn các tập hợp trên trục số ta được:

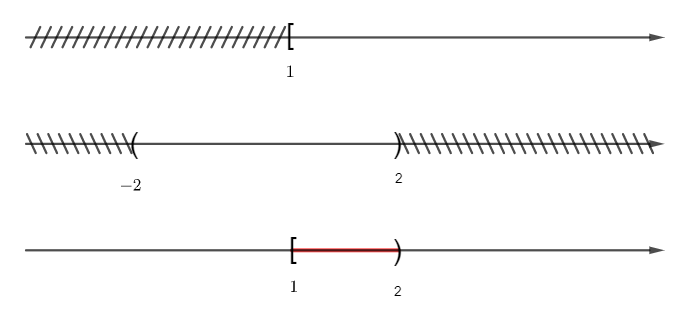
Vậy A ∩ B = [1; 2).

Câu 5. Cho A = {0; 1; 2; 3; 4} và B = {2; 3; 4; 5; 6}. Tập hợp (A \ B) ∪ (B \ A) bằng?

A. {5; 6};

B.  {2; 3; 4};

C. {1; 2};

D. {0; 1; 5; 6}.

Hướng dẫn giải

Đáp án đúng là: D

Ta có A \ B = {0; 1} và B \ A = {5; 6}.

Khi đó: (A \ B) ∪ (B \ A) = {0; 1; 5; 6}.

Câu 6: Số phần tử của tập hợp A = {k² + 1| k ∈ ℤ, |k| ≤ 2} bằng

A. 1;

B. 5;

C. 3;

D. 2.

Hướng dẫn giải

Đáp án đúng là: C

Ta có |k| ≤ 2

⇔ – k ≤ 2 hoặc k ≤ 2

⇔ k ≥ – 2 hoặc k ≤ 2

⇒ – 2 ≤ k ≤ 2

Mà k ∈ ℤ nên k ∈ {– 2; – 1; 0; 1; 2}.

⇒ k² + 1 ∈ {1; 2; 5}.

Do đó A = {1; 2; 5}. Vì vậy tập hợp A có 3 phần tử.

Câu 7: Cho hai tập hợp (1; 3) và [2; 4]. Giao của hai tập hợp đã cho là

A. (2; 3];                             

B. (2; 3);                             

C. [2; 3);                             

D. [2; 3].

Hướng dẫn giải

Đáp án đúng là: C

Ta biểu diễn các tập hợp đã cho trên trục số ta được:

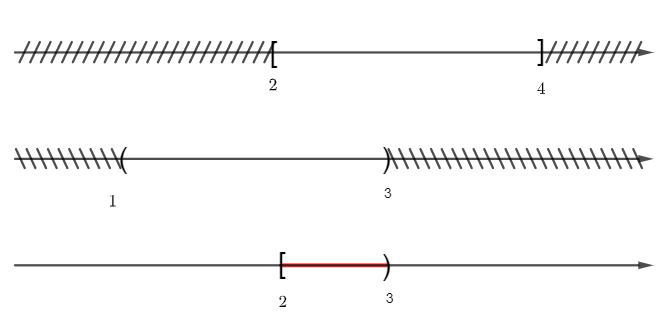
Vì vậy (1; 3) ∩ [2; 4] = [2; 3).

Câu 8: Hình vẽ sau đây (phần không bị gạch) là biểu diễn của tập hợp nào?

A. (– ∞; – 2) ∪ [5; +∞);    

B. (– ∞; – 2) ∪ (5; +∞);    

C. (– ∞; – 2] ∪ (5; +∞);

D. (– ∞; – 2] ∪ [5; +∞).

Hướng dẫn giải

Đáp án đúng là: D

Từ việc quan sát vào hình vẽ ta thấy phần không bị gạch chéo biểu diễn cho tập hợp:

(– ∞; – 2) ∪ [5; +∞).

Câu 9. Lớp 10A₁ có 6 học sinh giỏi Toán, 4 học sinh giỏi Lý, 5 học sinh giỏi Hóa, 2 học sinh giỏi Toán và Lý, 3 học sinh giỏi Toán và Hóa, 2 học sinh giỏi Lý và Hóa, 1 học sinh giỏi cả 3 môn Toán, Lý, Hóa. Số học sinh giỏi ít nhất một môn (Toán, Lý, Hóa) của lớp 10A₁ là:

A. 15;                                  

B. 23;                                  

C. 7;                                    

D. 9.

Hướng dẫn giải

Đáp án đúng là: D

Gọi T là tập hợp các bạn học sinh giỏi Toán, khi đó |T| = 6;

L là tập hợp các bạn học sinh giỏi Lý, khi đó |L| = 4;

H là tập hợp các bạn học sinh giỏi Hóa, khi đó |H| = 5.

Do đó ta có:

T ∩ L là tập hợp các bạn học sinh vừa giỏi môn Toán vừa giỏi Lý nên |T ∩ L| = 2;

T ∩ H là tập hợp các bạn học sinh vừa giỏi môn Toán vừa giỏi Hóa nên |T ∩ H| = 3;

H ∩ L là tập hợp các bạn học sinh vừa giỏi môn Hóa vừa giỏi Lý nên |H ∩ L| = 2.

T ∩ L ∩ H là tập hợp các bạn học sinh vừa giỏi môn Toán vừa giỏi Lý và vừa giỏi Hóa nên |T ∩ L ∩ H | = 1.

Tập hợp số học sinh giỏi ít nhất một môn là T ∪ L ∪ H. Khi đó:

|T ∪ L ∪ H| = |T| + |L| + |H| – |T ∩ L| – |T ∩ H| – |H ∩ L| + |T ∩ L ∩ H |

= 6 + 4 + 5 – 2 – 3 – 2 + 1 = 9.

Vậy có 9 học sinh của lớp 10A₁ vừa giỏi môn Toán vừa giỏi Lý và vừa giỏi Hóa.

Câu 10. Cặp số (x; y) nào sau đây là nghiệm của bất phương trình 5x – 3y ≤ 2?

A.  (0; – 2);                

B.  (3; 0);                    

C.  (2; 1);                    

D.  (– 1; – 1).

Hướng dẫn giải

Đáp án đúng là: D

+) Với (0; – 2) thay x = 0 và y = – 2 vào 5x – 3y ≤ 2 ta được:

5.0 – 3.(– 2) ≤ 2 ⇔ 6 ≤ 2 là một mệnh đề sai.

Do đó (0; – 2) không là nghiệm của bất phương trình.

+) Với (3; 0) thay x = 3 và y = 0 vào 5x – 3y ≤ 2 ta được:

5.3 – 3.0 ≤ 2 ⇔ 15 ≤ 2 là một mệnh đề sai.

Do đó (3; 0) không là nghiệm của bất phương trình.

+) Với (2; 1) thay x = 2 và y = 1 vào 5x – 3y ≤ 2 ta được:

5.2 – 3.1 ≤ 2 ⇔ 7 ≤ 2 là một mệnh đề sai.

Do đó (2; 1) không là nghiệm của bất phương trình.

+) Với (– 1; – 1) thay x = – 1 và y = – 1 vào 5x – 3y ≤ 2 ta được:

5.(– 1) – 3.(– 1) ≤ 2 ⇔ – 2  ≤ 2 là một mệnh đề đúng.

Do đó (– 1; – 1) không là nghiệm của bất phương trình.

Câu 11. Bất phương trình nào sau đây không là bất phương trình bậc nhất một ẩn?

A. 8 – $\sqrt{2}$x ≤ 0; 

B. 4x – 3 > 0;    

C. $\frac{1}{3}$x – 3 < 0;

D.  (x + 1)² ≥ 1.

Hướng dẫn giải

Đáp án đúng là: D

Ta thấy bất phương trình ở các đáp án A, B, C đều có dạng của bất phương trình bậc nhất hai ẩn.

Còn ý d là bất phương trình bậc 2. Do đó D không là bất phương trình bậc nhất một ẩn.

Câu 12. Phần mặt phẳng không bị gạch chéo trong hình vẽ bên (kể cả biên) là biểu diễn hình học tập nghiệm của hệ bất phương trình nào dưới đây?

A. $\left\{\begin{array}{l}x-y\ge 0\\ x+2y\le 4\end{array}\right.$;           

B. $\left\{\begin{array}{l}x-y\le 0\\ x+2y\ge 4\end{array}\right.$;

C. $\left\{\begin{array}{l}x-y\ge 0\\ x+2y\ge 4\end{array}\right.$ 

D. $\left\{\begin{array}{l}x-y\le 0\\ x+2y\le 4\end{array}\right.$.

Hướng dẫn giải

Đáp án đúng là: A

+) Gọi đường thẳng đi qua hai điểm có tọa độ (4; 0) và (0; 2) có dạng d₁: y = ax + b (a ≠ 0).

Thay lần lượt  tọa độ các điểm vào phương trình y = ax + b ta được hệ phương trình:

$\left\{\begin{array}{l}a.4+b=0\\ a.0+b=2\end{array}\right.\iff \left\{\begin{array}{l}a=-\frac{1}{2}\\ b=2\end{array}\right.$(thỏa mãn)

Suy ra d₁: y = $-\frac{1}{2}$x + 2 ⇔ x + 2y = 2.

Lấy điểm O(0; 0) không thuộc d₁, ta có: 0 + 2.0 = 0 < 2 và điểm O thuộc miền nghiệm của bất phương trình kể cả biên nên ta có x + 2y ≤ 2 (1).

+) Gọi đường thẳng đi qua O(0; 0) và là phân giác của góc phần tư thứ nhất và thứ hai có dạng d₂: y = x hay x – y = 0.

Lấy điểm M(1; 0) không thuộc d₂, ta có: 1 – 0 = 1 > 0 và điểm M thuộc miền nghiệm của bất phương trình kể cả biên nên ta có x – y ≥ 0 (2).

Từ (1) và (2) ta có hệ bất phương trình: $\left\{\begin{array}{l}x-y\ge 0\\ x+2y\le 4\end{array}\right.$.

Câu 13. Cho sin35° ≈ 0,57. Giá trị của sin145° gần với giá trị nào nhất sau đây:

A. 0,57;    

B. 1;

C. $\frac{\sqrt{2}}{2}$;

D. 0,15.

Hướng dẫn giải

Đáp án đúng là: A

Ta có 35° + 145° = 180°

⇒ sin35° = sin (180° – 145°) = sin145°

⇒ sin145° = sin35° ≈ 0,57.

Câu 14. Tính giá trị biểu thức: A = cos 0° + cos 40° + cos 120° + cos 140°

A. $\frac{1}{2}$;        

B. – 0,5;   

C. 1;

D. 0.

Hướng dẫn giải

Đáp án đúng là: A

A = cos 0° + cos 40° + cos 120° + cos 140°

= 1 + cos 40° – $\frac{1}{2}$ – cos 40°

= $\frac{1}{2}$.

Câu 15. Cho tam giác ABC, ta có các đẳng thức:

(I) sin$\frac{A}{2}$ = sin$\frac{B+C}{2}$;

(II) tan$\frac{A}{2}$ = cot$\frac{B+C}{2}$;

(III) sinA = sin(B + C).

Có bao nhiêu đẳng thức đúng?

A. $\frac{1}{2}$;        

B. – 0,5;   

C. 1;

D. 0.

Hướng dẫn giải

Đáp án đúng là: C

Xét tam giác ABC, ta có:

$\widehat{A}+\widehat{B}+\widehat{C}=180°$ ⇒ $\widehat{A}=180°-\left(\widehat{B}+\widehat{C}\right)$

⇒ sinA = sin(180°– (B + C)) = sin(B + C). Do đó (III) đúng.

Ta lại có: $\frac{\widehat{A}+\widehat{B}+\widehat{C}}{2}=90°$⇒$\frac{\widehat{A}}{2}=90°-\frac{\widehat{B}+\widehat{C}}{2}$

Khi đó: 

sin$\frac{A}{2}$ = sin$\left(90°-\frac{B+C}{2}\right)$ = cos$\frac{B+C}{2}$. Do đó (I) sai.

tan$\frac{A}{2}$ = tan$\left(90°-\frac{B+C}{2}\right)$ = cot$\frac{B+C}{2}$. Do đó (II) đúng.

Vậy có 2 phát biểu đúng.

Câu 16. Cho điểm M(x₀; y₀) nằm trên đường tròn đơn vị thỏa mãn $\widehat{xOM}=\alpha$. Khi đó phát biểu nào dưới đây là sai?

A. sinα = x₀;      

B. cosα = x₀;      

C. tanα = $\frac{y_0}{x_0}$;

D. cotα = $\frac{x_0}{y_0}$.

Hướng dẫn giải

Đáp án đúng là: A

Điểm M(x₀; y₀) nằm trên đường tròn đơn vị thỏa mãn $\widehat{xOM}=\alpha$ nên ta có:

sinα = y₀;

cosα = x₀;

tanα = $\frac{y_0}{x_0}$;

cotα = $\frac{x_0}{y_0}$.

Do đó A là đáp án sai.

Câu 17. Trong các công thức dưới đây, công thức nào sai về cách tính diện tích tam giác ABC? Biết AB = c, AC = b, BC = a, h_a, h_b, h_c lần lượt là các đường cao kẻ từ đỉnh A, B, C, r là bán kính đường tròn nội tiếp, R là bán kính đường tròn ngoại tiếp tam giác ABC.

A. S_ABC = pr;     

B. S_ABC = $\frac{1}{2}$c.a.sinA;

C. S_ABC = $\sqrt{p(p-a)(p-b)(p-c)}$;

D. S_ABC = $\frac{abc}{4R}$.

Hướng dẫn giải

Đáp án đúng là: B

Các công thức tính diện tích tam giác ABC là:

S_ABC = pr; S_ABC = $\frac{abc}{4R}$;

S_ABC = a.h_a = b.h_b = c.h_c;

S_ABC = $\frac{1}{2}$c.a.sinB = $\frac{1}{2}$c.b.sinA = $\frac{1}{2}$a.b.sinC;

S_ABC = $\sqrt{p(p-a)(p-b)(p-c)}$.

Do đó B sai.

Câu 18. Cho tam giác ABC, có các cạnh AB = c, AC = b, BC = a. Định lí sin được phát biểu:

A. $\frac{a}{\text{cos}A}=\frac{b}{\cos B}=\frac{c}{\cos C}$;       

B. $\frac{a}{\text{sin}A}=\frac{b}{\sin B}=\frac{c}{\sin C}$;         

C. a.cosA = b.cosB = c.cosC;

D. a.sinA = b.sinB = c.sinC.

Hướng dẫn giải

Đáp án đúng là: B

Xét tam giác ABC, định lí sin được phát biểu như sau: $\frac{a}{\text{sin}A}=\frac{b}{\sin B}=\frac{c}{\sin C}$

Do đó B đúng.

Câu 19. Cho tam giác ABC có BC = 50 cm, $\widehat{B}=65°,\widehat{C}=45°$. Tính (làm tròn kết quả đến hàng phần mười theo đơn vị xăng – ti – mét). Chu vi của tam giác ABC là:

A. 135,84;

B. 67,92;  

C. 131,91;

D. 65,96.

Hướng dẫn giải

Đáp án đúng là: B

Xét tam giác ABC, có:

$$\begin{gathered} \widehat{A}+\widehat{B}+\widehat{C}=180° \\ \Rightarrow \widehat{A}=180°-\widehat{B}-\widehat{C}=180°-65°-45°=70° \end{gathered}$$.

Áp dụng định lí sin trong tam giác ABC, có:

$\frac{BC}{\sin A}=\frac{AB}{\sin C}=\frac{AC}{\sin B}$

⇔ $\frac{50}{\sin 70}=\frac{AB}{\sin 45°}=\frac{AC}{\sin 65°}$

⇒ AB = $\frac{50.\sin 45°}{\sin 70°}\approx 37,6$

⇒ AC = $\frac{50.\sin 65°}{\sin 70°}\approx 48,2$

Khi đó chu vi tam giác ABC là:

50 + 37,6 + 48,2 = 135,8.

Câu 20. Một người đứng ở vị trí A trên nóc một ngôi nhà cao 8m đang quan sát một cây cao cách ngôi nhà 25m và đo được $\widehat{BAC}=65°$. Chiều cao của cây gần với kết quả nào nhất sau đây?

A. 38m;    

B. 39m;    

C. 19m;

D. 20m.

Hướng dẫn giải

Đáp án đúng là: A

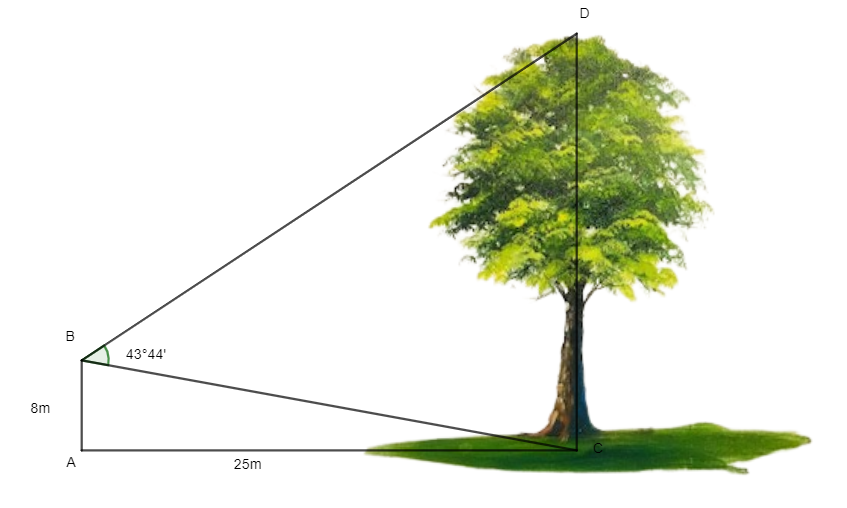
Đặt các điểm A, B, C, D như trên hình vẽ, khi đó:

Xét tam giác ABC vuông tại A, có:

tan $\widehat{ABC}=\frac{AC}{AB}=\frac{25}{8}\Rightarrow \widehat{ABC}\approx 72°15\text{'}$

⇒ $\widehat{ABD}=\widehat{ABC}+\widehat{CBD}\approx 72°15\text{'}+43°44\text{'}=115°59\text{'}$

Vì AB // CD nên $\widehat{BDC}=180°-\widehat{ABD}\approx 64°1\text{'}$

Xét tam giác BDC, có:

$$\begin{gathered} \frac{BC}{\sin \widehat{CBD}}=\frac{BC}{\sin \widehat{D}} \\ \iff BC=\frac{BC.\sin \widehat{D}}{\sin \widehat{CBD}}=\frac{\sqrt{689}.\sin 64°1\text{'}}{\sin 43°44\text{'}}\approx 20,2 \end{gathered}$$.

Vậy độ dài cây khoảng 20m.

Câu 21. Đẳng thức nào sau đây, mô tả đúng hình vẽ bên?

A. $3\overrightarrow{AI}+\overrightarrow{AB}=\overrightarrow{0}$.

B. $\overrightarrow{BI}+3\overrightarrow{BA}=\overrightarrow{0}$.

C. $3\overrightarrow{IA}+\overrightarrow{IB}=\overrightarrow{0}$. 

D. $\overrightarrow{AI}+3\overrightarrow{AB}=\overrightarrow{0}$.

Hướng dẫn giải

Đáp án đúng là: A

Theo hình vẽ, ta có:

+) AB = 3AI

Hai vectơ $\overrightarrow{AB}$ và $\overrightarrow{AI}$ nằm trên cùng một đường thẳng nên chúng cùng phướng tuy nhiên vectơ $\overrightarrow{AB}$ hướng từ trái sang phải, còn vectơ $\overrightarrow{AI}$ hướng từ phải sang trái nên vectơ $\overrightarrow{AB}$ và $\overrightarrow{AI}$ ngược hướng.

Do đó ta có: $\overrightarrow{AB}=-3\overrightarrow{AI}$ hay $3\overrightarrow{AI}+\overrightarrow{AB}=\overrightarrow{0}$. Do đó A đúng và D sai.

+) Hai vectơ $\overrightarrow{IB}$ và $\overrightarrow{IA}$ cùng hướng và IB = 4IA nên $\overrightarrow{IB}=4\overrightarrow{IA}$ hay $4\overrightarrow{IA}-\overrightarrow{IB}=\overrightarrow{0}$. Do đó C sai.

+) Hai vectơ $\overrightarrow{BI}$ và $\overrightarrow{BA}$ cùng hướng và BI = $\frac{4}{3}$BA nên $\overrightarrow{BI}=\frac{4}{3}\overrightarrow{BA}$ hay $4\overrightarrow{BA}-3\overrightarrow{BI}=\overrightarrow{0}$. Do đó B sai.

Câu 22: Cho hình chữ nhật ABCD. Hãy chọn khẳng định đúng.

A. $\overrightarrow{AB}=\overrightarrow{AD}$.                       

B. $\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}$.               

C. $\left|\overrightarrow{AB}\right|=\left|\overrightarrow{AD}\right|$.                     

D. $\overrightarrow{AB}=\overrightarrow{CD}$.

Hướng dẫn giải

Đáp án đúng là: B

Vì ABCD là hình chữ nhật nên ta có: AB // CD, AD // BC, AB = CD, AD = BC.

⇒ $\overrightarrow{AB}=\overrightarrow{DC}\ne \overrightarrow{AD}$ và $\left|\overrightarrow{AB}\right|=\left|\overrightarrow{DC}\right|$.  Do đó A, C và D sai.

Vì ABCD là hình chữ nhật nên ABCD cũng là hình bình hành nên $\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}$

Câu 23. Cho hình bình hành ABCD với điểm K thỏa mãn $\overrightarrow{KA}+\overrightarrow{KC}=\overrightarrow{AB}$ thì

A. K là trung điểm của AC.                       

B. K là trung điểm của AD.

C. K là trung điểm của AB.                        

D. K là trung điểm của BD.

Hướng dẫn giải

Đáp án đúng là: B

Gọi O là giao điểm của AC và BD nên O là trung điểm của AC. Khi đó $\overrightarrow{OA}+\overrightarrow{OC}=\overrightarrow{0}$

Ta có: $\overrightarrow{KA}+\overrightarrow{KC}=\overrightarrow{AB}$

$\iff \overrightarrow{KO}+\overrightarrow{OA}+\overrightarrow{KO}+\overrightarrow{OC}=\overrightarrow{AB}$

$\iff 2\overrightarrow{KO}=\overrightarrow{AB}$

$\iff \overrightarrow{KO}=\frac{1}{2}\overrightarrow{AB}$

Suy ra KO // AB và KO = $\frac{1}{2}$AB

Do đó K là điểm nằm trên đường thẳng song song với AB, đi qua O và bằng một nửa độ dài AB, hơn nữa phải cùng hướng với vectơ $\overrightarrow{AB}$ nên K là trung điểm của AD.

Câu 24. Cho tam giác đều ABC có AB = a, M là trung điểm của BC. Khi đó $\left|\overrightarrow{MA}+\overrightarrow{AC}\right|$ bằng

A. $\frac{a}{4}$. 

B. 2a.   

C. $\frac{a}{2}$.   

D. a.

Hướng dẫn giải

Đáp án đúng là: C

Xét tam giác ABC, có:

$\overrightarrow{MA}+\overrightarrow{AC}=\overrightarrow{MC}$ (quy tắc ba điểm)

⇒ $\left|\overrightarrow{MA}+\overrightarrow{AC}\right|=\left|\overrightarrow{MC}\right|=MC=\frac{1}{2}BC=\frac{a}{2}.$

Câu 25. Cho hình bình hành ABCD. Mệnh đề nào sau đây đúng?

A. $\overrightarrow{AC}=\overrightarrow{BC}$.                

B. $\overrightarrow{AD}=\overrightarrow{CD}$.               

C. $\overrightarrow{AB}=\overrightarrow{DC}$.               

D. $\overrightarrow{AC}=\overrightarrow{BD}$.

Hướng dẫn giải

Đáp án đúng là: C

Vì ABCD là hình bình hành nên AB // CD, AD // BC và AD = CD, AD = BC nên $\overrightarrow{AB}=\overrightarrow{DC}$.

Câu 26. Cho hình chữ nhật ABCD tâm O. Gọi M, N lần lượt là trung điểm của các cạnh AB, AD. Chọn khẳng định đúng trong các khẳng định sau:

A. $\overrightarrow{AB}=\overrightarrow{CD}$;                       

B. $\overrightarrow{AN}=\overrightarrow{MO}$;

C. $\overrightarrow{OC}=\overrightarrow{OD}$;                       

D. $\overrightarrow{AM}=\overrightarrow{BM}$.

Hướng dẫn giải

Đáp án đúng là: B

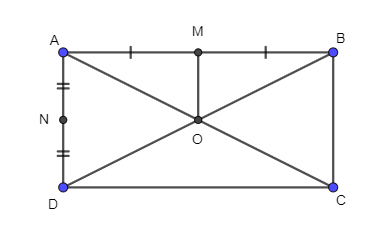
+) Ta có M là trung điểm của AB nên ta có: $\overrightarrow{AM}=-\overrightarrow{BM}$. Do đó D sai.

+) Ta lại có ABCD là hình chữ nhật nên AB // CD, AB = CD và hai vectơ $\overrightarrow{AB}$, $\overrightarrow{DC}$cùng hướng nên $\overrightarrow{AB}=\overrightarrow{DC}$. Do đó A sai.

+) Xét tam giác ABD, có:

M là trung điểm của AB

O là trung điểm của BD

⇒ MO là đường trung bình của tam giác ABD

⇒ MO = $\frac{1}{2}$AD

Mà AN = ND = $\frac{1}{2}$AD nên MO = AN.

Ta thấy $\overrightarrow{MO}$ và $\overrightarrow{AN}$ cùng hướng nên $\overrightarrow{MO}=\overrightarrow{AN}$. Do đó B đúng.

Hai vectơ $\overrightarrow{OC}$ và $\overrightarrow{OD}$ không cùng phương nên không thể bằng nhau. Do đó C sai.

Câu 27. Phát biểu nào sau đây là sai?

A. Độ dài của vectơ là khoảng cách giữa điểm đầu và điểm cuối của vectơ đó.

B. Vectơ là đoạn thẳng có hướng.

C. Hai vectơ cùng hướng thì cùng phương.

D. Hai vectơ cùng phương thì cùng hướng.

Hướng dẫn giải

Đáp án đúng là: D

Vectơ là đoạn thẳng có hướng và độ dài của vectơ là khoảng cách giữa điểm đầu và điểm cuối của vectơ đó. Do đó A và B đúng.

Hai vectơ cùng hướng thì cùng phương còn ngược lại hai vectơ cùng phương thì chưa chắc cùng hướng. Do đó C đúng, D sai.

Câu 28. Cho hình thang MNPQ, MN // PQ, MN = 2PQ. Phát biểu nào dưới đây là đúng?

A. $\overrightarrow{MN}=2\overrightarrow{PQ}$;

B. $\overrightarrow{MQ}=2\overrightarrow{NP}$;                     

C. $\overrightarrow{MN}=-2\overrightarrow{PQ}$;                   

D. $\overrightarrow{MQ}=-2\overrightarrow{NP}$.

Hướng dẫn giải

Đáp án đúng là: C

Vì MNPQ là hình thang và MN // PQ, MN = 2PQ suy ra $\overrightarrow{MN}$ và $\overrightarrow{QP}$ cùng hướng nên $\overrightarrow{MN}=2\overrightarrow{QP}$ hay $\overrightarrow{MN}=-2\overrightarrow{PQ}$.

Vì MP và NQ không song song cũng không trùng nhau nên hai vectơ $\overrightarrow{MQ}$ và 2$\overrightarrow{NP}$không cùng phương nên không bằng nhau.

Câu 29. Cho tam giác đều ABC nội tiếp đường tròn tâm O bán kính bằng 1. Gọi M là điểm nằm trên đường tròn (O), độ dài vectơ $\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}$ bằng

A. 1;                                    

B. 6;                                    

C. $\sqrt{3}$;                                

D. 3.

Hướng dẫn giải

Đáp án đúng là: D

Ta có ABC là tam giác đều nên O là tâm đường tròn ngoại tiếp cũng là trọng tâm tam giác ABC. Do đó ta có: $\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{0}$.

Xét $\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow{MO}+\overrightarrow{OA}+\overrightarrow{MO}+\overrightarrow{OB}+\overrightarrow{MO}+\overrightarrow{OC}$

$=3\overrightarrow{MO}+\left(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}\right)=3\overrightarrow{MO}$

⇒ $\left|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right|=\left|3\overrightarrow{MO}\right|=3\left|\overrightarrow{MO}\right|=3MO$

Vì M thuộc vào tâm đường tròn ngoại tiếp tam giác ABC nên MO = R = 1.

Vậy $\left|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right|=3MO=3$.

Câu 30. Cho tam giác ABC đều có cạnh bằng a, gọi H là trung điểm của cạnh BC. Độ dài của vectơ $2\left(\overrightarrow{HA}-\overrightarrow{HC}\right)$bằng

A. a;                                    

B. 2a;                                  

C. $\frac{a\sqrt{3}}{2}$; 

D. $a\sqrt{3}$.

Hướng dẫn giải

Đáp án đúng là: B

Ta có: $\overrightarrow{HA}-\overrightarrow{HC}=\overrightarrow{CA}$

⇒ $\left|2\left(\overrightarrow{HA}-\overrightarrow{HC}\right)\right|=2\left|\left(\overrightarrow{HA}-\overrightarrow{HC}\right)\right|=2\left|\overrightarrow{CA}\right|=2a$

PHẦN II. TỰ LUẬN

Bài 1 (1,0 điểm).

a) Cho tập hợp A = {x ∈ ℝ | x² = 2} và B = {x ∈ ℕ| x² + 5x – 6 = 0}. Tìm tập hợp A ∩ B và A ∪ B.

b) Cho tập hợp A = (m ; m + 2] và B = [– 1 ; 5]. Tìm m để A ⊂ B.

Lời giải

a) Xét x² = 2 $\iff \left[\begin{array}{l}x=\sqrt{2}\\ x=-\sqrt{2}\end{array}\right.$

Vì $\sqrt{2};-\sqrt{2}\in ℝ$ nên $A=\left\{\sqrt{2};-\sqrt{2}\right\}$.

Xét x² + 5x – 6 = 0 $\iff \left[\begin{array}{l}x=1\\ x=-6\end{array}\right.$

Vì 1 ∈ ℕ, – 6 ∉ ℕ nên B = {1}.

Khi đó: A ∩ B = ∅ và A ∪ B = $\left\{\sqrt{2};1;-\sqrt{2}\right\}$.

b) Để A ⊂ B thì  ⇔ – 1 ≤ m ≤ 3.

Vậy với – 1 ≤ m ≤ 3 thì A ⊂ B.

Bài 2 (1,5 điểm). Tìm giá trị nhỏ nhất của biểu thức F(x; y) = – 2x + y trên miền nghiệm của hệ bất phương trình $\left\{\begin{array}{l}x-y\ge -2\\ x+y\le 4\\ x-5y\le -2\end{array}\right.$.

Lời giải

+) Xét bất phương trình x – y ≥ – 2

Vẽ đường thẳng d₁: x – y = – 2 ;

Lấy điểm O(0; 0) ∉ d₁ có 0 – 0 = 0 > – 2. Do đó O(0; 0) thuộc vào miền nghiệm của bất phương trình.

Do đó miền nghiệm D₁ là nửa mặt phẳng có bờ là đường thẳng d₁ chứa điểm O và kể cả đường thẳng d₁.

+) Xét bất phương trình x + y ≤ 4

Vẽ đường thẳng d₂: x + y = 4;

Lấy điểm O(0; 0) ∉ d₂ có 0 + 0 = 0 < 4. Do đó O(0; 0) thuộc vào miền nghiệm của bất phương trình.

Do đó miền nghiệm D₂ là nửa mặt phẳng có bờ là đường thẳng d₂ chứa điểm O và kể cả đường thẳng d₂.

+) Xét bất phương trình x – 5y ≤ – 2

Vẽ đường thẳng d₃: x – 5y = – 2;

Lấy điểm O(0; 0) ∉ d₃ có 0 – 5.0 = 0 > – 2. Do đó O(0; 0) không thuộc vào miền nghiệm của bất phương trình.

Do đó miền nghiệm D₃ là nửa mặt phẳng có bờ là đường thẳng d₃ không chứa điểm O và kể cả đường thẳng d₃.

Vậy miền nghiệm của hệ bất phương trình là giao của ba miền nghiệm D₁, D₂ và D₃ là miền trong của tam giác ABC có A(1; 3), B(3; 1), C(– 2; 0).

Giá trị nhỏ nhất của biểu thức F(x; y) đạt được trên các đỉnh của tam giác ABC.

Ta có:

Tại điểm A(1; 3) ta có: F(x; y) = – 2.1 + 3 = 1.

Tại điểm B(3; 1) ta có: F(x; y) = – 2.3 + 1 = – 5.

Tại điểm C(– 2; 0) ta có: F(x; y) = – 2.(– 2) + 0 = 4.

Vậy giá trị nhỏ nhất của F(x; y) = – 5.

Bài 3 (1,5 điểm).

a) Cho 4 điểm M,N, P, Q bất kỳ, chứng minh rằng $\overrightarrow{MP}+\overrightarrow{NQ}-\overrightarrow{NP}=\overrightarrow{MQ}$.

b) Cho hình bình hành ABCD. Gọi E là điểm thỏa mãn $4\overrightarrow{DE}=\overrightarrow{DC}$ và G là trọng tâm tam giác ABE. Đường thẳng AG cắt BC tại F.  Biểu diễn $\overrightarrow{AG}$ theo $\overrightarrow{AB}$, $\overrightarrow{AD}$ và tính tỉ số $\frac{BF}{BC}$.

Lời giải

a) Xét vế trái của đẳng thức, ta có :

$\overrightarrow{MP}+\overrightarrow{NQ}-\overrightarrow{NP}=\overrightarrow{MQ}+\overrightarrow{QP}+\overrightarrow{PQ}=\overrightarrow{MQ}+\overrightarrow{0}=\overrightarrow{MQ}.$

b) Gọi M là trung điểm của BE, khi đó ta có: $\overrightarrow{AG}=\frac{2}{3}\overrightarrow{AM}$

Ta lại có: $\overrightarrow{AB}+\overrightarrow{AE}=2\overrightarrow{AM}\iff \overrightarrow{AM}=\frac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AE}\right)$

⇒ $$\begin{gathered} \overrightarrow{AG}=\frac{2}{3}\overrightarrow{AM}=\frac{2}{3}.\frac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AE}\right) \\ =\frac{1}{3}\left(\overrightarrow{AB}+\overrightarrow{AE}\right)=\frac{1}{3}\left(\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{DE}\right) \end{gathered}$$

    $$\begin{gathered} =\frac{1}{3}\left(\overrightarrow{AB}+\overrightarrow{AD}+\frac{1}{4}\overrightarrow{DC}\right) \\ =\frac{1}{3}\left(\overrightarrow{AB}+\overrightarrow{AD}+\frac{1}{4}\overrightarrow{AB}\right) \\ =\frac{1}{3}\left(\frac{5}{4}\overrightarrow{AB}+\overrightarrow{AD}\right) \\ =\frac{5}{12}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AD} \end{gathered}$$

Giả sử $\frac{BF}{BC}=a$. Khi đó $\overrightarrow{BF}=a\overrightarrow{BC}$

Ta có: 

$$\begin{gathered} \overrightarrow{\text{AF}}=\overrightarrow{AB}+\overrightarrow{BF}=\overrightarrow{AB}+a\overrightarrow{BC} \\ =\overrightarrow{AB}+a\left(\overrightarrow{AC}-\overrightarrow{AB}\right) \\ =\left(1-a\right)\overrightarrow{AB}+a\overrightarrow{AC} \\ =(\mathrm{1}\mathrm{-}a)\overrightarrow{\mathit{A}\mathit{B}}+a\overrightarrow{\mathit{A}\mathit{C}} \\ =(\mathrm{1}\mathrm{-}a)\overrightarrow{\mathit{A}\mathit{B}}+a(\overrightarrow{AB}\mathrm{+}\overrightarrow{AD}) \\ =\overrightarrow{\mathit{A}\mathit{B}}+a\overrightarrow{\mathit{A}\mathit{D}} \end{gathered}$$

Vì A, G, F thẳng hàng nên tồn tại số thực k > 0 để $\overrightarrow{AG}=k\overrightarrow{AF}$

⇔ $\frac{5}{12}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AD}=k\left(\overrightarrow{AB}+a\overrightarrow{AD}\right)$

⇔ $\frac{5}{12}\left(\overrightarrow{AB}+\frac{4}{5}\overrightarrow{AD}\right)=k\left(\overrightarrow{AB}+a\overrightarrow{AD}\right)$

⇒ $k=\frac{5}{12}$ và $a=\frac{4}{5}$.

Vậy tỉ số $\frac{BF}{BC}=\frac{4}{5}$.

Xem thêm các đề thi Giữa học kì 1 Toán học 10 hay, chi tiết khác:

Đề thi Giữa học kì 1 Toán 10 Kết nối tri thức (Có đáp án)...

Đề thi giữa kì 1 Toán 10 Chân trời sáng tạo (Có đáp án)...

Xem thêm các đề thi Học kì 1 Toán học 10 hay, chi tiết khác:

Đề thi học kì 1 Toán 10 Kết nối tri thức (Có đáp án)...

Đề thi Học kì 1 Toán 10 Chân trời sáng tạo (Có đáp án)...

Đề thi học kì 1 Toán 10 Cánh diều (Có đáp án)...