Toptailieu.vn biên soạn và giới thiệu Top 30 Đề thi Giữa học kì 2 Toán 10 (Cánh diều 2024) có đáp án gồm các đề thi được tuyển chọn và tổng hợp từ các đề thi môn Toán THPT trên cả nước có hướng dẫn giải chi tiết giúp học sinh làm quen với các dạng đề, ôn luyện để đạt kết quả cao trong kì thi sắp tới. Mời các bạn đón xem:
Top 30 Đề thi Giữa học kì 2 Toán 10 (Cánh diều 2024) có đáp án
Đề thi Giữa học kì 2 Toán 10 Cánh diều (Có đáp án) - Đề số 01
Phòng Giáo dục và Đào tạo ...
Đề thi Giữa học kì 2 Toán 10
Năm học 2022 - 2023
Môn: Toán học 10
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
Câu 1 (5,0 điểm): Giải các bất phương trình sau:
a)
b)
c)
Câu 2 (1,5 điểm): Tìm để bất phương trình có nghiệm tùy ý.
Câu 3 (2,0 điểm): Giải hệ bất phương trình: .
Câu 4 (1,5 điểm): Tìm để phương trình có nghiệm âm.
Lời giải chi tiết
Câu 1 (VD) - Bất phương trình
Phương pháp:
a) Tìm ĐKXĐ. Lập bảng xét dấu để tìm tập nghiệm của bất phương trình.
b) Quy đồng và áp dụng: Nếu và thì .
c) Phá dấu giá trị tuyệt đối, giải các bất phương trình nhận được và kết luận tập nhiệm:
Cách giải:
Giải các bất phương trình sau:
a)
ĐKXĐ:
Ta có bảng xét dấu:
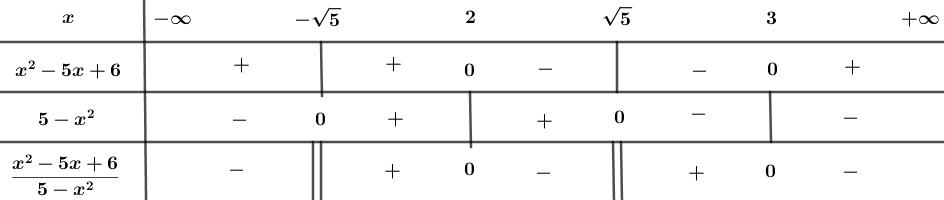
Để thì
Vậy bất phương trình có tập nghiệm .
b)
ĐKXĐ:
Vậy bất phương trình có tập nghiệm .
c)
TH1:
Bất phương trình
Mà .
TH2:
Bất phương trình
Mà .
Kết hợp cả hai trường hợp ta được tập nghiệm của bất phương trình là:
Câu 2 (VD) - Bất phương trình
Phương pháp:
Áp dụng:
Cách giải:
Tìm để bất phương trình có nghiệm tùy ý.
Bất phương trình có nghiệm tùy ý khi và chỉ khi .
+) luôn đúng
+)
Vậy .
Câu 3 (VD) - Bất phương trình và hệ bất phương trình một ẩn
Phương pháp:
Giải từng bất phương trình sau đó kết hợp nghiệm.
Cách giải:
Giải hệ bất phương trình: .
ĐKXĐ:
Vậy hệ bất phương trình có tập nghiệm .
Câu 4 (VDC) - Phương trình quy về phương trình bậc hai
Phương pháp:
Xác định điều kiện của để phương trình có hai nghiệm trái dấu và hai nghiệm âm.
Cách giải:
Tìm để phương trình có nghiệm âm.
+) : PT trở thành: (không thỏa mãn)
+)
với mọi
Phương trình có hai nghiệm phân biệt với .
PT có nghiệm âm PT có hai nghiệm trái dấu .
PT có nghiệm âm
Vậy thì phương trình có nghiệm âm.
Đề thi Giữa học kì 2 Toán 10 Cánh diều (Có đáp án) - Đề số 02
Phòng Giáo dục và Đào tạo ...
Đề thi Giữa học kì 2 Toán 10
Năm học 2022 - 2023
Môn: Toán học 10
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
Câu 1 (4,0 điểm): Giải các bất phương trình sau:
a)
b)
c)
d)
Câu 2 (1,5 điểm): Cho hàm số và .
Tìm tất cả các giá trị của tham số để , .
Câu 3 (1,5 điểm): Cho tam giác với . Hãy tính diện tích tam giác và các bán kính đường tròn ngoại tiếp, nội tiếp của tam giác .
Câu 4 (2,5 điểm): Trong mặt phẳng tọa độ , cho hai điểm , và đường thẳng ( là tham số)
a) Lập phương trình tổng quát của đường thẳng đi qua và vuông góc với .
b) Tìm tọa độ điểm đối xứng với qua .
c) Tìm tọa độ điểm trên sao cho cách một khoảng bằng .
Câu 5 (0,5 điểm): Giải phương trình .
Lời giải chi tiết
Câu 1 (VD) - Bất phương trình
Phương pháp:
a) Đưa về phương trình bậc hai và lập bảng xét dấu.
b) Tìm ĐKXĐ. Quy đồng sau đó lập bảng xét dấu.
c) Áp dụng
d) Áp dụng
Cách giải:
Giải các bất phương trình sau:
a)
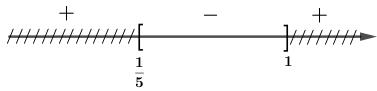
Vậy bất phương trình có tập nghiệm là .
b)
ĐKXĐ:
Ta có bảng xét dấu:
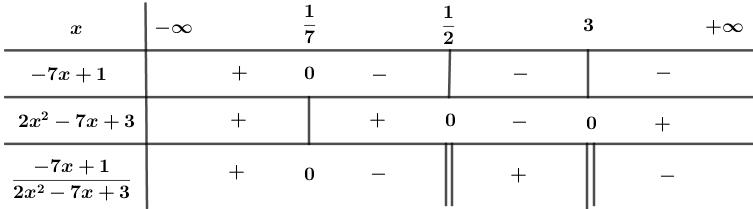
Vậy bất phương trình có tập nghiệm là .
c)
Vậy tập nghiệm của bất phương trình là .
d)
Vậy bất phương trình có tập nghiệm là .
Câu 2 (VD) - Bất phương trình
Phương pháp:
Đưa biểu thức về dạng .
Cách giải:
Cho hàm số và .
Tìm tất cả các giá trị của tham số để , .
Theo đề bài, ta có:
TH1 :
Bất phương trình trở thành (luôn đúng)
TH2 :
Để
Kết hợp hai trường hợp trên, ta được
Vậy thì , .
Câu 3 (VD) - Các hệ thức lượng trong tam giác và giải tam giác
Phương pháp:
Tính nửa chu vi của tam giác .
Áp dụng các công thức:
+ Công thức Hê-rông
+ ,
Cách giải:
Cho tam giác với . Hãy tính diện tích tam giác và các bán kính đường tròn ngoại tiếp, nội tiếp của tam giác .
Đặt .
Áp dụng công thức Hê-rông ta có:
Ta lại có:
Câu 4 (VD) - Phương trình đường thẳng
Phương pháp:
a)
đi qua nhận là VTPT
b) Giả sử là trung điểm của . Tọa độ điểm là nghiệm của hệ phương trình .
c) sau đó áp dụng công thức tính độ dài véc tơ để tìm tọa độ điểm M .
Cách giải:
Trong mặt phẳng tọa độ , cho hai điểm , và đường thẳng ( là tham số)
a) Lập phương trình tổng quát của đường thẳng đi qua và vuông góc với .
Vì .
Phương trình tổng quát của đường thẳng đi qua có VTPT là :
Vậy phương trình tổng quát của đường thẳng .
b) Tìm tọa độ điểm đối xứng với qua .
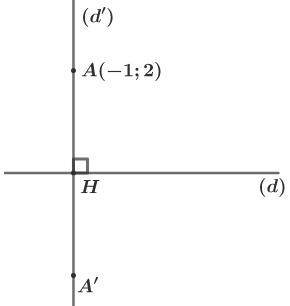
Theo đề bài, đối xứng với qua nên là đường trung trực của .
mà và
Giả sử là trung điểm của .
Tọa độ điểm là nghiệm của hệ phương trình:
Vì là trung điểm của nên
c) Tìm tọa độ điểm trên sao cho cách một khoảng bằng .
Có .
Theo đề bài, ta có:
+) Với
+) Với
Vậy hoặc thì cách một khoảng bằng .
Câu 5 (VD) - Phương trình quy về phương trình bậc nhất, phương trình bậc hai
Phương pháp:
+ Tìm ĐKXĐ
+ Biến đổi phương trình đã cho về dạng .
Cách giải:
ĐKXĐ:
Ta có:
Dấu “” xảy ra khi và chỉ khi:
Vậy phương trình có nghiệm .
Xem thêm đề thi các môn lớp 10 bộ sách Cánh diều hay, có đáp án chi tiết:
Top 10 đề thi giữa Học kì 2 Ngữ văn 10 (Cánh diều 2024) có đáp án
Top 10 đề thi giữa Học kì 2 Vật lí 10 (Cánh diều 2024) có đáp án
Top 50 Đề thi Giữa học kì 2 Hóa học 10 (Cánh diều 2024) tải nhiều nhất
Top 50 Đề thi Giữa học kì 2 Lịch sử 10 (Cánh diều 2024) tải nhiều nhất
Top 10 đề thi giữa Học kì 2 Sinh học 10 (Cánh diều 2024) có đáp án
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.