Toptailieu.vn xin giới thiệu 40 câu trắc nghiệm Mệnh đề toán học (Cánh diều) có đáp án - Toán 10 chọn lọc, hay nhất giúp học sinh lớp 10 ôn luyện kiến thức để đạt kết quả cao trong các bài thi môn Toán.
Mời các bạn đón xem:
10 câu trắc nghiệm Phương trình đường thẳng (Cánh diều) có đáp án - Toán 10
Câu 1: Cho đường thẳng Δ có một vectơ chỉ phương là u→(-3;5). Vectơ nào dưới đây không phải là VTCP của Δ?
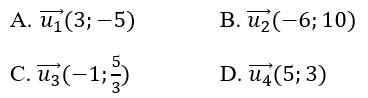
Đáp án D
Các vectơ khác vectơ – không, cùng phương (tọa độ tỉ lệ) với u→ thì đều là VTCP của đường thẳng Δ.
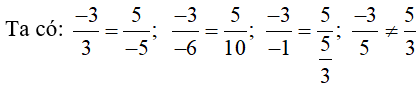
Do đó vectơ ở phương án D không phải là VTCP.
Câu 2: Phương trình tham số của đường thẳng Δ đi qua điểm M(2; 3) và có hệ số góc k = 4 là:
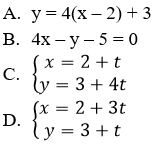
Đáp án C
Đường thẳng Δ có hệ số góc k = 4 nên có vectơ chỉ phương u→ = (1;4). Do đó C là phương án đúng.
Chú ý. Học sinh có thể nhầm sâng các loại phương trình khác của đường thẳng như các phương án ở A và B. Đây đều là phương trình của đường thẳng nhưng không là phương trình tham số.
Câu 3: Cho hai đường thẳng d1: 3x – 4y +2 = 0 và d2: mx +2y – 3 = 0. Hai đường thẳng song song với nhau khi:
A. m = 3 B. m=3/2
C. m=-3/2 D. m = - 3
Đáp án C
Hai đường thẳng song song khi:
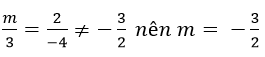
Câu 4: Cho hai đường thẳng d1: y = 3x – 1 và
Góc giữa hai đường thẳng là:
A. α = 30o B. α=45o C. α=60o D. α=90o
Đáp án B
Hai đường thẳng lần lượt có các vectơ chỉ phương là u1→=(1;3) và u2→=(-1;2) nên ta có
![]()
Do đó góc giữa hai đường thẳng là α = 45o.
Câu 5: Cho điểm A(-2; 1) và hai đường thẳng d1: 3x – 4y + 2 = 0 và d2: mx + 3y – 3 = 0. Giá trị của m để khoảng cách từ A đến hai đường thẳng bằng nhau là:
A. m=±1
B. m = 1 và m = 4
C. m=±4
D. m = - 1 và m = 4
Đáp án C
Sử dụng công thức khoảng cách ta có:
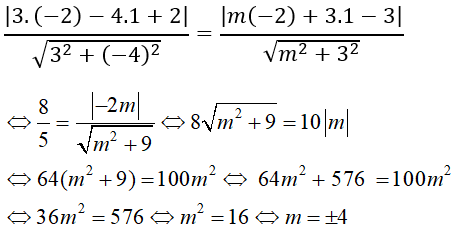
Chú ý. Học sinh có thể thử lại các phương án được đưa ra để chọn đáp án đúng, tuy nhiên sẽ tốn nhiều thời gian hơn là làm bài toán trực tiếp.
Câu 6: Cho tam giác ABC với A(-2; 3), B(1; 4), C(5; -2). Phương trình đường trung tuyến AM của tam giác là:
A. x – 2y + 8 = 0
B. 2x + 5y – 11 = 0
C. 3x – y + 9 = 0
D. x + y – 1 = 0
Đáp án B

Câu 7: Cho tam giác ABC có phương trình các cạnh AB: 3x – y + 4 = 0, AC: x + 2y – 4 = 0, BC: 2x + 3y – 2 = 0. Khi đó diện tích của tam giác ABC là:
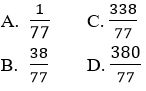
Đáp án C
Bằng việc lần lượt giải các hệ phương trình bậc nhất hai ẩn, ta có tọa độ các đỉnh của tam giác là
![]()
Ta có công thức tính diện tích tam giác ABC là:
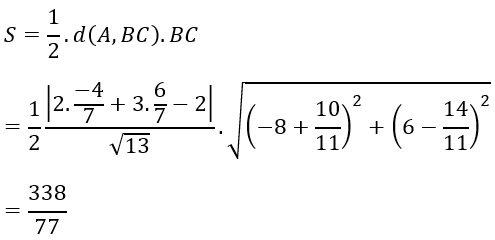
Câu 8: Cho điểm A(3; 5) và các đường thẳng d1: y = 6, d2: x = 2. Số đường thẳng d qua A tạo với các đường thẳng d1, d2 một tam giác vuông cân là
A. 0 B. 1 C. 2 D. Vô số
Đáp án B
Do d1 ⊥ d2 nên d có tính chất trên thì d tạo với tía Ox góc 45o hoặc 135o. Mà d1, d2 cắt nhau tại B(2; 6) nên AB tạo với Ox góc 135o. Do đó, trong hai đường thẳng kề trên chỉ có đường thẳng tạo với Ox góc 45o thỏa mãn yêu cầu, còn đường thẳng tạo với Ox góc 135o phải loại bỏ do khi đó không tạo thành tam giác. Đáp án là phương án B.
Chú ý. Học sinh thường quên xét góc của AB tạo với Ox và chọn luôn phương án là hai đường thẳng.
Câu 9: Có bao nhiêu vectơ pháp tuyến của một đường thẳng?
A. 0 B. 1 C. 2 D. Vô số
Đáp án D
Nếu n→ là vectơ pháp tuyến của một đường thẳng thì kn→ (với k ≠ 0) đều là vectơ pháp tuyến của đường thẳng.
Vì thế có vô số vectơ pháp tuyến của một đường thẳng.
Câu 10: Cho đường thẳng Δ có vectơ chỉ phương là u→=(2;-3). Vectơ nào sau đây không phải là vectơ chỉ phương của Δ?
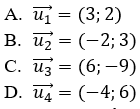
Đáp án A
Nếu u→ là vectơ chỉ phương của một đường thẳng thì ku→ (với k ≠ 0) đều là vectơ chỉ phương của đường thẳng đó.
Vì vậy các vectơ có tọa độ tỉ lệ với u→=(2;-3) đều là vectơ chỉ phương.
Ta có:
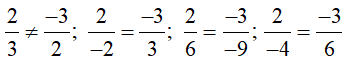
Do đó, trong các vectơ đã cho có u1→ không phải là vectơ chỉ phương của đường thẳng ∆.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.