Toptailieu.vn xin giới thiệu 40 câu trắc nghiệm Mệnh đề toán học (Cánh diều) có đáp án - Toán 10 chọn lọc, hay nhất giúp học sinh lớp 10 ôn luyện kiến thức để đạt kết quả cao trong các bài thi môn Toán.

Mời các bạn đón xem:

10 câu trắc nghiệm Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng (Cánh diều) có đáp án - Toán 10

Câu 1. Xét vị trí tương đối của hai đường thẳng:

d1: x – 2y + 2 = 0 và d2: – 3x + 6y – 10 = 0

A. Trùng nhau;

B. Song song;

C. Vuông góc với nhau;

D. Cắt nhau nhưng không vuông góc nhau.

Đáp án đúng là: B

Xét hệ phương trình: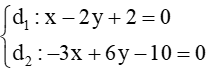 

Giải hệ phương trình: 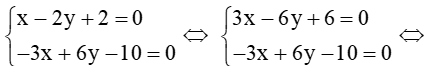–4 = 0 (vô lý)

Vậy suy ra hệ phương trình trên vô nghiệm

$\Rightarrow$Hai đường thẳng song song.

Câu 2. Xét vị trí tương đối của hai đường thẳng:

$d_1$: 3x – 2y – 3 = 0 và $d_2$: 6x – 2y – 8 = 0

A. Trùng nhau;

B. Song song;

C. Vuông góc với nhau;

D. Cắt nhau nhưng không vuông góc nhau.

Đáp án đúng là: D

Ta có: $d_1$: 3x – 2y – 3 = 0 có VTPT là $\overrightarrow{n_1}$ = (3; – 2) và $d_2$: 6x – 2y – 8 = 0 có VTPT là $\overrightarrow{n_2}$ = (6; – 2).

Ta có: $\frac{3}{6}\ne \frac{-2}{-2}$ nên hai vectơ $\overrightarrow{n_1}$ và $\overrightarrow{n_2}$ không cùng phương.

Do đó đường thẳng d₁ và d₂ cắt nhau.

Ta lại có $\overrightarrow{n_1}.\overrightarrow{n_2}=3.6+\left(-2\right).\left(-2\right)=22\ne 0$ nên d₁ và d₂ không vuông góc với nhau.

Vậy hai đường thẳng cắt nhau nhưng không vuông góc.

Câu 3. Xét vị trí tương đối của hai đường thẳng $d_1:\frac{x}{3}-\frac{y}{4}=1$ và $d_2$: 3x + 4y – 8 = 0.

A. Trùng nhau;

B. Song song;

C. Vuông góc với nhau;

D. Cắt nhau nhưng không vuông góc nhau.

Đáp án đúng là: C

Phương trình $d_1$ có vectơ pháp tuyến ${\overrightarrow{n}}_1=\left(\frac{1}{3};-\frac{1}{4}\right)$

Phương trình $d_2$ có vectơ pháp tuyến ${\overrightarrow{n}}_2=\left(3;4\right)$

Ta có: $\frac{\frac{1}{3}}{3}\ne \frac{-\frac{1}{4}}{4}$${\overrightarrow{n}}_1;{\overrightarrow{n}}_2$ không cùng phương và ${\overrightarrow{n}}_1\cdot {\overrightarrow{n}}_2$ = $\frac{1}{3}$.3 + $\left(-\frac{1}{4}\right)$.4 = 0. Như vậy hai vectơ pháp tuyến của hai đường thẳng vuông góc với nhau, suy ra hai đường thẳng vuông góc với nhau.

Câu 4.Tìm m để hai đường thẳng d₁ và d₂ vuông góc với nhau:

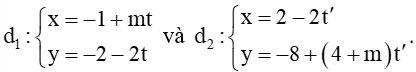
A. m = $-2+\sqrt{2}$;

B. m = $-2-\sqrt{2}$;

C. m = 2;

D. không tồn tại m.

Đáp án đúng là: D

Đường thẳng 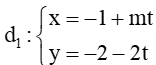 có VTCP là $\overrightarrow{u_1}=\left(m;-2\right)$;

Đường thẳng 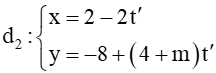 có VTCP là $\overrightarrow{u_2}=\left(-2;4+m\right)$.

Để hai đường thẳng d₁ và d₂ vuông góc với nhau thì $\overrightarrow{u_1}$ và $\overrightarrow{u_2}$ không cùng phương và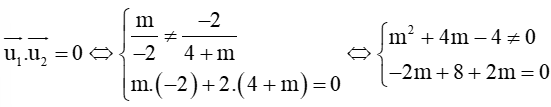 

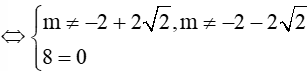
Vậy không tồn tại m thỏa mãn yêu cầu bài toán.

Câu 5. Cho đường thẳng 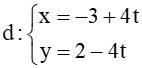. Đường thẳng nào sau đây trùng với đường thẳng d.

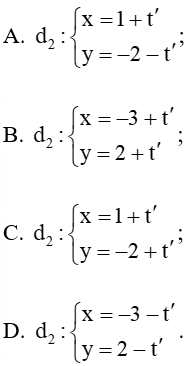
Đáp án đúng là: A

Đường thẳng 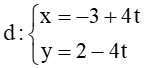 có VTCP là $\overrightarrow{u_d}$ = (4; – 4) = 4.(1; – 1). Suy ra VTCP của đường thẳng d cũng là vectơ có tọa độ (1; – 1).

Với t = 1 thì 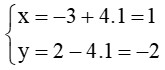. Do đó đường thẳng d đi qua điểm có tọa độ (1; – 2).

Vì vậy đường thẳng d trùng với đường thẳng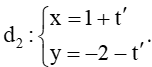 

Câu 6. Tính góc tạo bởi giữa hai đường thẳng: $d_1$: 2x – y – 3 = 0 và $d_2$: x – 3y + 8 = 0

A. ${30}^{\text{o}}.$

B. ${45}^{\text{o}}.$

C. ${60}^{\text{o}}.$

D. ${135}^{\text{o}}.$

Đáp án đúng là: B

Ta có:

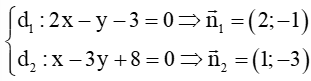 với ${\overrightarrow{n}}_1$; ${\overrightarrow{n}}_2$ lần lượt là các vectơ pháp tuyến của đường thẳng $d_1$; $d_2$.

Áp dụng công thức góc giữa hai đường thẳng, ta có:

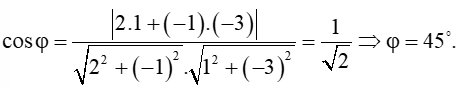
Câu 7. Tìm giá trị âm của m để góc tạo bởi giữa hai đường thẳng $d_1$: 7x – 3y + 2 = 0 và $d_2$: 2x + 5my +1 = 0 bằng 45°.

A. – 1;

B. $\frac{4}{25}$;

C. $-\frac{4}{25}$;

D. 1.

Đáp án đúng là: A

Ta có:

 với ${\overrightarrow{n}}_1$; ${\overrightarrow{n}}_2$ lần lượt là vectơ pháp tuyến của đường thẳng $d_1$; $d_2$.

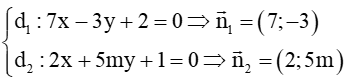
Áp dụng công thức góc giữa hai đường thẳng:

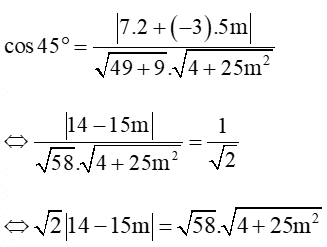
⇔ 2(196 – 420m + 225m²) = 58(4 + 25m²)

⇔ 392 – 840m + 450m² = 232 + 1450m²

⇔ 1000m² + 840m – 160 = 0

⇔ m = $\frac{4}{25}$ hoặc m = – 1

Vậy giá trị âm của m thỏa mãn điều kiện bài toán là m = – 1.v

Câu 8. Tính góc tạo bởi giữa hai đường thẳng:

$d_1:2x+2\sqrt{3}y+4=0$ và $d_2$: y – 4 = 0

A. ${30}^{\text{o}};$

B. ${45}^{\text{o}};$

C. ${60}^{\text{o}};$

D. ${90}^{\text{o}}.$

Đáp án đúng là: A

Ta có:

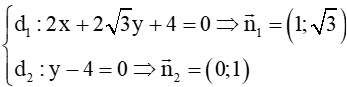 với ${\overrightarrow{n}}_1$; ${\overrightarrow{n}}_2$ lần lượt là vectơ pháp tuyến của đường thẳng $d_1$; $d_2$.

Áp dụng công thức góc giữa hai đường thẳng ta có:

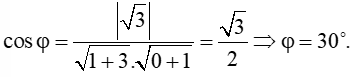
Câu 9. Tính góc tạo bởi giữa hai đường thẳng: $d_1:x+\sqrt{3}y+6=0$ và $d_2$: x + 1 = 0

A.${30}^{\text{o}};$

B. ${45}^{\text{o}};$

C. ${60}^{\text{o}};$

D. ${90}^{\text{o}}.$

Đáp án đúng là: C

Ta có:

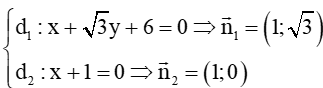 với ${\overrightarrow{n}}_1$; ${\overrightarrow{n}}_2$ lần lượt là vectơ pháp tuyến của đường thẳng $d_1$; $d_2$.

Áp dụng công thức góc giữa hai đường thẳng ta có:

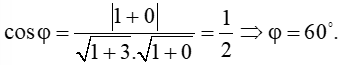
Câu 10. Góc tạo bởi hai đường thẳng nào dưới đây bằng 90°

A. $d_1$: 6x – 5y + 4 = 0 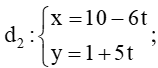và 

B.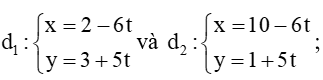 

C. d₁: x – 2y + 4 = 0 và d₂: y + 1 = 0;

D. 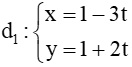 và d₂: 3x + 2y – 4 = 0.

Đáp án đúng là: A

+) Đường thẳng $d_1$: 6x – 5y + 4 = 0 có VTPT là $\overrightarrow{n_1}=\left(6;-5\right)$

Đường thẳng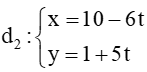 có VTCP là $\overrightarrow{u_2}=\left(-6;5\right)$ nên VTCP là $\overrightarrow{n_2}=\left(5;6\right)$

Ta có: $\overrightarrow{n_1}.\overrightarrow{n_2}=5.6+6.\left(-5\right)=0$. Do đó d₁ ⊥ d₂ hay góc giữa hai đường thẳng bằng 90°.

+) Đường thẳng 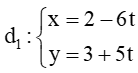có VTCP là $\overrightarrow{u_1}=\left(-6;5\right)$

Đường thẳng 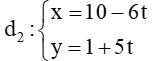 có VTCP là $\overrightarrow{u_2}=\left(-6;5\right)$

Ta có: $\frac{-6}{5}=\frac{-6}{5}$ nên $\overrightarrow{u_1}$ và $\overrightarrow{u_2}$ cùng phương. Do đó hai đường thẳng d₁ song song hoặc trùng d₂. Do đó góc giữa hai đường thẳng bằng 0°.

+) Đường thẳng d₁: x – 2y + 4 = 0 có VTPT là $\overrightarrow{n_1}=\left(1;-2\right)$

Đường thẳng d₂: y + 1 = 0 có VTPT là $\overrightarrow{n_2}=\left(0;1\right)$

Áp dụng công thức tính góc giữa hai đường thẳng ta được:

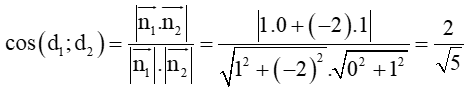
⇒ (d₁ ; d₂) ≈ 26°34’.

+) Đường thẳng 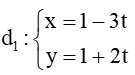có VTCP là $\overrightarrow{u_1}=\left(-3;2\right)$ nên VTCP là $\overrightarrow{n_1}=\left(2;3\right)$

Đường thẳng d₂: 3x + 2y – 4 = 0 có VTPT là $\overrightarrow{n_2}=\left(3;2\right)$

Áp dụng công thức tính góc giữa hai đường thẳng ta được:

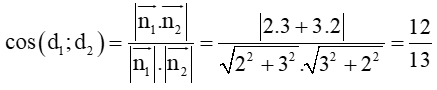
⇒ (d₁ ; d₂) ≈ 22°37’.