Với giải Câu hỏi trang 88 Toán 10 Tập 1 Kết nối tri thức trong Bài 14: Các số đặc trưng đo độ phân tán học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:
Toán 10 Kết nối tri thức trang 88 Bài 14: Các số đặc trưng đo độ phân tán
Bài 5.11 trang 88 Toán lớp 10 Tập 1: Mỗi khẳng định sau đúng hay sai?
(1) Nếu các giá trị của mẫu số liệu càng tập trung quanh giá trị trung bình thì độ lệch chuẩn càng lớn.
(2) Khoảng biến thiên chỉ sử dụng thông tin của giá trị lớn nhất và bé nhất , bỏ qua thông tin của các giá trị còn lại.
(3) Khoảng tứ phân vị có sử dụng thông tin của giá trị lớn nhất, giá trị bé nhất.
(4) Khoảng tứ phân vị chính là khoảng biến thiên của nửa dưới mẫu số liệu đã sắp xếp.
(5) Các số đo độ phân tán đều không âm.
Lời giải:
Nếu các giá trị của mẫu số liệu càng tập trung quanh giá trị trung bình thì độ phân tán nhỏ nên độ lệch chuẩn càng nhỏ. Do đó (1) sai.
Khoảng biến thiên chỉ sử dụng thông tin của giá trị lớn nhất và bé nhất , bỏ qua thông tin của các giá trị còn lại. Do đó (2) đúng.
Khoảng tứ phân vị là hiệu số giữa tứ phân vị thứ ba và tứ phân vị thứ nhất. Do đó (3) sai.
Về bản chất, khoảng tứ phân vị là khoảng biến thiên của 50% số liệu chính giữa của mẫu số liệu đã sắp xếp. Do đó (4) sai.
Các số đo độ phân tán gồm:
Khoảng biến thiên là hiệu của giá trị lớn nhất và giá trị nhỏ nhất nên không âm.
Khoảng tứ phân vị là hiệu của tứ phân vị thứ ba và tứ phân vị thứ nhất mà dãy số liệu được sắp xếp theo thứ tự không giảm nên không âm.
Phương sai và độ lệch chuẩn đều không âm.
Do đó (5) đúng.
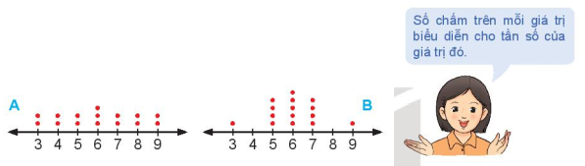
Không tính toán, hãy cho biết:
a) Hai mẫu số liệu này có cùng khoảng biến thiên và số trung bình không?
b) Mẫu số liệu nào có phương sai lớn hơn?
Lời giải:
a)
Mẫu số liệu thứ nhất và mẫu số liệu thứ hai có giá trị lớn nhất là 9 và giá trị nhỏ nhất là 3. Do đó hai mẫu số liệu này có cùng khoảng biến thiên.
Mẫu số liệu thứ nhất có xu hướng trung tâm là giá trị 6.
Mẫu số liệu thứ hai các giá trị tập trung nhiều xung quanh ba giá trị 5, 6, 7 nên số trung bình sẽ khoảng 6.
Do đó hai mẫu số liệu có cùng giá trị trung bình.
b)
Mẫu số liệu thứ nhất các giá trị rải đều từ 3 đến 9 nên độ phân tán nhỏ. Còn mẫu số liệu thứ hai có độ phân tán lớn hơn nên phương sai của mẫu số liệu thứ hai lớn hơn.
a) Nhân mỗi giá trị của mẫu số liệu với 2.
b) Cộng mỗi giá trị của mẫu số liệu với 2.
Lời giải:
a) Gọi các giá trị dương của mẫu số liệu ban đầu theo thứ tự từ bé đến lớn là: a; b; c; d; e; f; g; h; i; k.
Số trung bình cộng của mẫu số liệu là:
Phương sai:
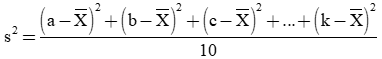
Độ lệch chuẩn:
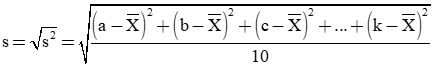
Giá trị lớn nhất là k, giá trị nhỏ nhất là a. Khi đó khoảng biến thiên: R = k – a.
Vì n = 10 nên trung vị là trung bình cộng hai giá trị chính giữa:
Nửa mẫu số liệu bên trái có tứ phân vị thứ nhất là
Nửa mẫu số liệu bên phải có tứ phân vị thứ ba là .
Khi đó khoảng tứ phân vị là:
Nhân mỗi giá trị của mẫu số liệu với 2 ta được dãy số liệu mới theo thứ tự từ bé đến lớn là: 2a; 2b; 2c; 2d; 2e; 2f; 2g; 2h; 2i; 2k.
Số trung bình cộng của mẫu số liệu là:
Phương sai:
Độ lệch chuẩn:
Giá trị lớn nhất là k, giá trị nhỏ nhất là a. Khi đó khoảng biến thiên: R’ = 2k – 2a = 2R.
Ta có: tứ phân vị thứ nhất là và tứ phân vị thứ ba là . Khi đó khoảng tứ phân vị là:
Vậy các khoảng biến thiên, độ lệch chuẩn, khoảng tứ phân vị của dãy số liệu mới bằng hai lần các khoảng biến thiên, độ lệch chuẩn, khoảng tứ phân vị ban đầu.
b)
Các giá trị dương của mẫu số liệu khi cộng thêm mẫu số liệu với 2 ta được: a + 2; b + 2; c + 2; d + 2; e + 2; f + 2; g + 2; h + 2; i + 2; k + 2.
Số trung bình cộng của mẫu số liệu là:
Phương sai:
Độ lệch chuẩn:
Giá trị lớn nhất là k, giá trị nhỏ nhất là a. Khi đó khoảng biến thiên: R’ = 2 + k – (2 + a) = k – a = R.
Ta có: tứ phân vị thứ nhất là
và tứ phân vị thứ ba là
.
Khi đó khoảng tứ phân vị là:
Vậy các khoảng biến thiên, độ lệch chuẩn, khoảng tứ phân vị của dãy số liệu mới bằng các khoảng biến thiên, độ lệch chuẩn, khoảng tứ phân vị ban đầu.
Giá trị nhỏ nhất bằng 2,5; Q1 = 36; Q2 = 60; Q3 = 100; giá trị lớn nhất bằng 205.
a) Tỉ lệ thành phố có thuế thuốc lá lớn hơn 36 là bao nhiêu?
b) Chỉ ra hai giá trị sao cho có 50% giá trị của mẫu số liệu nằm giữa hai giá trị này?
c) Tìm khoảng tứ phân vị của mẫu số liệu.
Lời giải:
a) Vì số các giá trị của số liệu n = 51 là số lẻ nên trung vị của số liệu là giá trị thứ 26.
Nửa bên trái số trung vị gồm 25 số liệu là số lẻ nên tứ phân vị thứ nhất là giá trị thứ 13 có giá trị là 36.
Do đó có 38 thành phố có thuế thuốc lá hơn 36.
Suy ra tỉ lệ các thành phố có thuế thuốc lá lớn hơn 36 là:
Vậy tỉ lệ các thành phố có thuế thuốc là lớn hơn 36 là: 74,51%.
b)
Tứ phân vị thứ nhất là giá trị thứ 13, tứ phân vị thứ ba là giá trị thứ 39.
Giữa hai giá trị là các giá trị thứ 13 đến giá trị thứ 39. Do đó có tất cả (39 – 13):1 + 1 = 27.
Mà
Vậy giữa hai giá trị Q1 = 36 và Q3 = 100 có 50% giá trị của mẫu số liệu nằm giữa hai giá trị này.
d) Khoảng tứ phân vị của mẫu số liệu này là: ∆Q = Q3 – Q1 = 100 – 36 = 64
2,977 3,155 3,920 3,412 4,236
2,593 3,270 3,813 4,042 3,387.
Hãy tìm khoảng biến thiên, khoảng tứ phân vị và độ lệch chuẩn cho mẫu số liệu này.
Lời giải:
Sắp xếp các giá trị của số liệu trên theo thứ tự từ bé đến lớn là:
2,593; 2,977; 3,155; 3,270; 3,387; 3,412; 3,813; 3,920; 4,042; 4,236. .
Ta có giá trị lớn nhất là 4,236 kg và giá trị nhỏ nhất là 2,593 kg.
Khi đó khoảng biến thiên là: R = 4,236 – 2,593 = 1,643.
Vì n = 10 là số chẵn nên trung vị là trung bình cộng của hai giá trị chính giữa: Q2 = (3,387 + 3,412):2 = 3,3995.
Nửa số liệu bên trái gồm 5 số liệu là một số lẻ nên tứ phân vị thứ nhất là: Q1 = 3,155.
Nửa số liệu bên phải gồm 5 số liệu là một số lẻ nên tứ phân vị thứ ba là: Q3 = 3,920.
Khoảng tứ phân vị là:
∆Q = Q3 – Q1 = 3,920 – 3,155 = 0,765.
Số trung bình cộng của mẫu số liệu là:
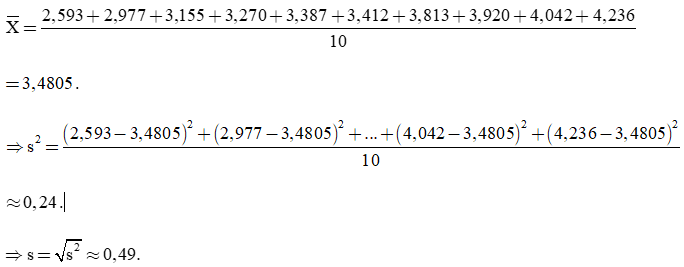
Vậy khoảng biến thiên R = 1,643, khoảng tứ phân vị ∆Q = 0,765; độ lệch chuẩn s ≈ 0,49.
7,8 3,2 7,7 8,7 8,6 8,4 7,2 3,6
5,0 4,4 6,7 7,0 4,5 6,0 5,4.
Hãy tìm các giá trị bất thường (nếu có) của mẫu số liệu trên.
Lời giải:
Sắp xếp dãy số liệu theo thứ tự không giảm, ta được:
3,2; 3,6; 4,4; 4,5; 5,0; 5,4; 6,0; 6,7; 7,0; 7,2; 7,7; 7,8; 8,4; 8,6; 8,7.
Vì n = 15 là số lẻ nên số trung vị là giá trị chính giữa Q2 = 6,7.
Nửa số liệu bên trái có 7 số liệu nên có tứ phân vị thứ nhất là Q1 = 4,5.
Nửa số liệu bên phải có 7 số liệu nên có tứ phân vị thứ hai là Q3 = 7,8.
Khoảng tứ phân vị là: ∆Q = Q3 – Q1 = 7,8 – 4,5 = 3,3.
Ta có: Q1 – 1,5ΔQ = 4,5 – 4,95 = -0,45 và Q3 + 1,5ΔQ = 7,8 + 4,95 = 12,75 nên trong mẫu số liệu đã cho không có giá trị nào bất thường.
Vậy mẫu số liệu đã cho không có giá trị nào bất thường.
Xem thêm các bài giải sách bài tập Toán lớp 10 Kết nối tri thức hay, chi tiết khác:
Câu hỏi mở đầu trang 84 Toán 10: Dưới đây là điểm trung bình môn học kì I của hai bạn An và Bình...
Luyện tập 1 trang 85 Toán 10: Mẫu số liệu sau cho biết chiều cao (đơn vị cm) của các bạn trong tổ...
Bài 5.11 trang 88 Toán lớp 10 Tập 1: Mỗi khẳng định sau đúng hay sai?...
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.