Mở đầu trang 6 Vật lí 11: Hằng ngày chúng ta thấy rất nhiều chuyển động, trong đó vật chuyển động qua lại quanh một vị trí cân bằng. Chuyển động của người chơi đu là một ví dụ như vậy (Hình 1.1).

Những chuyển động đó được gọi là dao động. Mô tả dao động như thế nào?

Lời giải:

Dao động là chuyển động mà vật chuyển động qua lại quanh một vị trí đặc biệt gọi là vị trí cân bằng.

Câu hỏi 1 trang 7 Vật lí 11: Dùng một lò xo, một quả cầu nhỏ bằng kim loại, sợi dây và giá thí nghiệm, thảo luận với bạn xây dựng phương án và thực hiện phương án tạo ra dao động của quả cầu treo ở một đầu lò xo.

Lời giải:

Xây dựng phương án: Treo quả cầu ở một đầu lò xo, đầu còn lại của lò xo treo lên giá thí nghiệm. Nối một sợi dây với quả cầu. Ban đầu, vật treo trên lò xo đứng yên, lò xo nằm trên trục thẳng đứng. Ta tác dụng một lực kéo nhỏ lên sợi dây theo phương thẳng đứng chiều từ trên xuống dưới.

Thực hiện phương án: Quan sát thấy lò xo dãn rồi co lần lượt, vật chuyển động qua lại quanh vị trí ban đầu (vị trí cân bằng). Như vậy, ta có được dao động của vật treo ở đầu lò xo.

Câu hỏi 2 trang 7 Vật lí 11: Nêu ví dụ về dao động mà bạn quan sát được trong thực tế

Lời giải:

Dây đàn ghita dao động sau khi gảy, màng trống dao động sau khi gõ vào, con lắc đồng hồ dao động, âm thoa dao động sau khi gõ vào, thuyền dao động (nhấp nhô lên xuống tại chỗ) trên mặt nước, …

Giải Vật lí 11 trang 8

Câu hỏi 1 trang 8 Vật lí 11: Với một cái thước mỏng đàn hồi, hãy đề xuất phương án tạo ra dao động tự do của thước và mô tả cách làm

Lời giải:

Giữ một đầu thước cố định, một đầu tự do (gắn/giữ một đầu thước trên mép bàn). Nhấn đầu thước tự do xuống một biên độ nhỏ quan sát được nhưng không làm thước bị biến dạng, không thể trở lại như ban đầu. Đầu thước sẽ chuyển động lên xuống quanh vị trí ban đầu (vị trí cân bằng), đó có thể xem là dao động tự do của đầu thước

Câu hỏi 2 trang 8 Vật lí 11: Nếu bỏ qua lực cản, chuyển động nào sau đây là dao động tự do:

A. Một con muỗi đang đập cánh

B. Tòa nhà rung chuyển trong trận động đất

C. Mặt trống rung động sau khi gõ

D. Bông hoa rung rinh trong gió nhẹ

Lời giải:

Đáp án C. Nếu không có lực cản, mặt trống sẽ chuyển động quanh vị trí cân bằng không ngừng sau tác động ban đầu là lực tác dụng khi gõ trống. Phương án a không đúng vì cánh của con muỗi chuyển động là nhờ lực mà cơ cánh tác dụng liên tục để đập cánh. Phương án b và phương án d không đúng vì các chuyển động này xảy ra trong quá trình chịu tác động liên tục không ngừng (trong trận động đất, khi gió thổi).

Câu hỏi trang 9 Vật lí 11: Từ đồ thị Hình 1.7, mô tả sự thay đổi li độ của xe theo thời gian

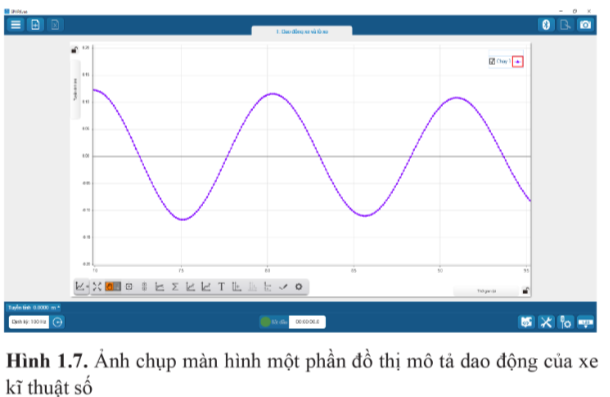
Lời giải:

Đồ thị là đồ thị hàm sin. Vật bắt đầu chuyển động tại vị trí có li độ lớn nhất, sau đó li độ giảm dần đến 0 rồi đến li độ nhỏ nhất. Li độ từ giá trị nhỏ nhất lại tăng dần đến 0 rồi đến giá trị lớn nhất. Sau đó, quá trình lặp lại, li độ từ giá trị lớn nhất giảm dần, … Sự thay đổi diễn ra tuần hoàn, theo chu kì.

Giải Vật lí 11 trang 10

Câu hỏi 1 trang 10 Vật lí 11: Tìm mối liên hệ giữa chu kì T và tần số f của dao động

Lời giải:

Chu kì của dao động là khoảng thời gian để vật thực hiện một dao động. Tần số của dao động là số dao động vật thực hiện được trong một giây.

Để tìm số dao động vật thực hiện được trong một giây, ta lấy thời gian 1s chia cho thời gian thực hiện mỗi dao động, nghĩa là $f=\frac{1}{T}$.

Câu hỏi 2 trang 10 Vật lí 11: Xác định biên độ, chu kì và tần số của dao động có đồ thị li độ thời gian được biểu diễn ở Hình 1.9

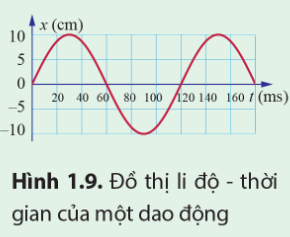
Lời giải:

Giá trị lớn nhất của li độ là 10 cm, do đó, biên độ dao động A = 10 cm.

Chu kì của dao động T = 120 ms = 0,12 s.

Tần số của dao động là: $f=\frac{1}{T}=\frac{1}{0,12}=\frac{25}{3}\approx 8,33$(Hz)

Giải Vật lí 11 trang 11

Câu hỏi 1 trang 11 Vật lí 11: Thế nào là dao động điều hòa?

Lời giải:

Dao động điều hòa là dao động trong đó li độ của vật là một hàm côsin (hay sin) của thời gian.

Câu hỏi 2 trang 11 Vật lí 11: Tần số góc và tần số của dao động điều hòa có liên hệ như thế nào

Lời giải:

Tần số góc ω (đơn vị rad/s) gấp (2π) lần so với tần số f (đơn vị Hz)

Câu hỏi trang 12 Vật lí 11: Dựa vào đồ thị Hình 1.12, xác định các đại lượng sau:

a. Tần số góc của dao động.

b. Biên độ của dao động.

c. Vận tốc cực đại của vật dao động.

d. Gia tốc cực đại của vật dao động.

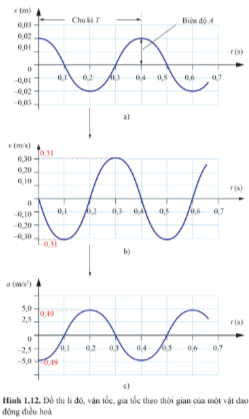
Lời giải:

a)     Chu kì của dao động là $T=0,4$ s.

Tần số góc của dao động là: $\omega =\frac{2\pi }{T}=\frac{2\pi }{0,4}=5\pi$ (rad/s).

b)    Biên độ của dao động là $A=0,02$ m.

c)     Vận tốc cực đại của vật là giá trị lớn nhất của vận tốc, $v_{max}=0,31$ m/s.

d)    Gia tốc cực đại của vật là giá trị lớn nhất của gia tốc, $a_{max}=0,49$ m/s².

Câu hỏi trang 13 Vật lí 11: Dựa vào độ dốc của đồ thị li độ - thời gian, ta có thể xác định vận tốc của xe kĩ thuật số tại mỗi thời điểm. Từ các số liệu này có thể vẽ được đồ thị hình sin biểu diễn sự liên hệ giữa vận tốc và thời gian (Hình 1.12b).

Ví dụ, trong Hình 1.12a, độ dốc của đồ thị li độ - thời gian bằng 0, vận tốc bằng 0. Khi t tăng từ 0 s đến 0,2 s, độ dốc âm, vận tốc có giá trị âm. Tại t = 0,2 s, độ dốc bằng 0 một lần nữa. Từ t = 0,2 s đến t = 0,4 s, độ dốc dương, vận tốc có giá trị dương. Độ dốc của đồ thị li độ - thời gian có độ lớn cực đại tại các thời điểm t = 0,1 s; 0,3 s; 0,5 s; …

Bằng cách tương tự, dựa vào độ dốc của đồ thị vận tốc – thời gian ở Hình 1.12b, ta có thể tìm được gia tốc của xe tại mỗi thời điểm và vẽ được đồ thị hình sin như Hình 1.12c.

Dựa vào các đồ thị ở Hình 1.12, tìm:

Các thời điểm gia tốc của xe bằng 0.

Các thời điểm gia tốc của xe cực đại.

Giải thích cách làm.

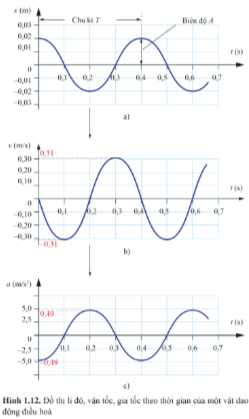
Lời giải:

Xác định độ dốc: Đặt mép thước tiếp xúc với đồ thị tại điểm cần xét, mép thước là tiếp tuyến của đồ thị tại điểm đó, độ dốc của đồ thị là độ dốc của đường thẳng tạo bởi mép thước.

Ta xác định được, độ dốc của đồ thị vận tốc – thời gian (Hình 1.12b) bằng 0 tại các thời điểm t = 0,1 s; 0,3 s; 0,5 s; … Do đó, tại các thời điểm này, gia tốc của vật bằng 0.

Độ dốc của đồ thị li độ - thời gian có độ lớn cực đại tại các thời điểm t = 0,2 s; 0,4 s; 0,6 s; … Do đó, tại các thời điểm này, gia tốc của vật đạt độ lớn cực đại.

Giải Vật lí 11 trang 14

Câu hỏi 1 trang 14 Vật lí 11: Xác định pha của dao động tại vị trí 3 và vị trí 4

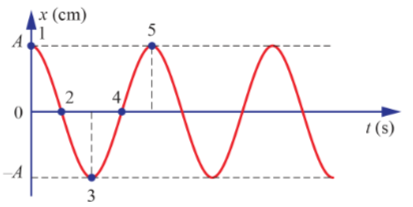
Lời giải:

Li độ $x=A\cos (\omega t+\phi )$

Tại thời điểm t = 0, li độ x = A sau đó li độ giảm dần, vật chuyển động theo chiều âm. Do đó, pha ban đầu của dao động là $\phi =0$.

Vật chuyển động trong thời gian T/2 đến vị trí 3, thực hiện nửa dao động tương ứng với góc $\pi$ rad.

Pha của dao động tại vị trí 3 là $\omega t+\phi =\pi +0=\pi$(rad).

Vật chuyển động trong thời gian $\frac{3T}{4}$ đến vị trí 3, thực hiện $\frac{3}{4}$ dao động tương ứng với góc $\frac{3\pi }{2}$ rad.

Pha của dao động tại vị trí 3 là $\omega t+\phi =\frac{3\pi }{2}+0=\frac{3\pi }{2}$ (rad).

Câu hỏi 2 trang 14 Vật lí 11: Một vật dao động điều hòa với phương trình li độ: $x=5\cos (10\pi t+\frac{\phi }{2})$(cm). Xác định pha của dao động tại thời điểm $\frac{1}{30}$s

Lời giải:

Pha của dao động tại thời điểm $t=\frac{1}{30}$ s là:

$10\pi t+\frac{\phi }{2}=10\pi .\frac{1}{30}+\frac{\phi }{2}=\frac{\pi }{3}+\frac{\phi }{2}$(rad).

Câu hỏi trang 15 Vật lí 11: Mô tả trạng thái của hai vật dao động ở thời điểm t3 và t4 trong đồ thị Hình 1.14

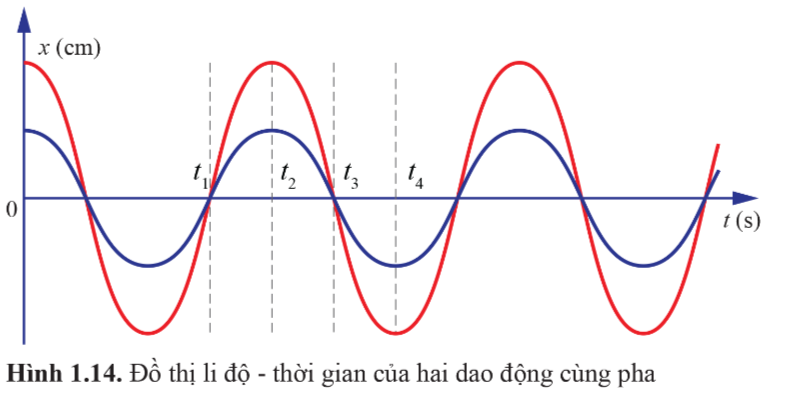
Lời giải:

Tại thời điểm t3, li độ của mỗi vật bằng 0, và đang giảm dần. Hai vật ở vị trí cân bằng, đạt tốc độ cực đại và đang chuyển động chậm dần theo chiều âm.

Tại thời điểm t4, li độ của mỗi vật có giá trị bằng – A (hai giá trị biên độ khác nhau), và đang tăng dần. Hai vật ở vị trí biên âm, vận tốc bằng không (đứng yên), sau đó chuyển động nhanh dần theo chiều dương.

Câu hỏi trang 16 Vật lí 11: Đồ thị Hình 1.18 biểu diễn hai dao động ngược pha. Dựa vào đồ thị, xác định độ lệch pha của hai dao động này

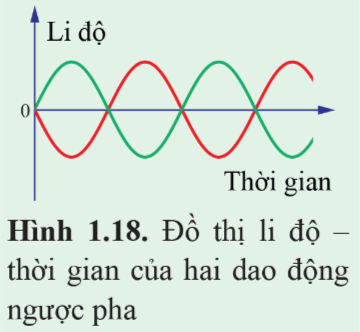
Lời giải:

Độ lệch thời gian khi hai vật cùng trạng thái là $\mathrm{\Delta }t=\frac{T}{2}$.

Độ lệch pha là: $\mathrm{\Delta }\phi =\frac{\mathrm{\Delta }t}{\mathrm{\Delta }T}=\frac{1}{2}$ dao động, tương ứng với πrad.

Vậy $\mathrm{\Delta }\phi =\pi$rad.