Toptailieu biên soạn và giới thiệu lời giải Toán 8 Bài 4 (Chân trời sáng tạo): Hình bình hành – Hình thoi hay, chi tiết sẽ giúp học sinh dễ dàng trả lời câu hỏi SGK Toán 8 Bài 4 từ đó học tốt môn Toán 8.

Toán 8 (Chân trời sáng tạo) Bài 4: Hình bình hành – Hình thoi

Giải Toán 8 trang 73 Tập 1

Khởi động trang 73 Toán 8 Tập 1: Quan sát hình chụp các mái nhà ở phố cổ Hội An, em thấy các cạnh đối của tứ giác ABCD có gì đặc biệt?

Lời giải:

Quan sát hình chụp các mái nhà ở phố cổ Hội An, ta thấy các cạnh đối của tứ giác ABCD vừa song song vừa bằng nhau (AB // DC, AB = DC và AD // BC, AD = BC).

1. Hình bình hành

Khám phá 1 trang 73 Toán 8 Tập 1: Hình 1a là hình ảnh của một thước vẽ truyền dùng để phóng to hay thu nhỏ một hình vẽ có sẵn. Dùng thước đo góc để đo số đo của các cặp góc ${\widehat{A}}_1$ và $D$, ${\widehat{C}}_1$ và $D$ của tứ giác ABCD (Hình 1b) rồi rút ra nhận xét về mối quan hệ giữa các cặp cạnh AB và CD; AD và BC.

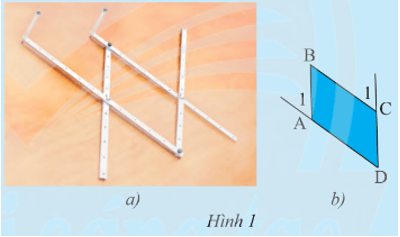
Lời giải:

Dùng thước đo góc ta xác định được ${\widehat{A}}_1=\widehat{D}$ và ${\widehat{C}}_1=\widehat{D}$.

Ta có ${\widehat{A}}_1=\widehat{D}$ và hai góc này ở vị trí đồng vị nên AB // CD.

${\widehat{C}}_1=\widehat{D}$ và hai góc này ở vị trí đồng vị nên AD // BC.

Giải Toán 8 trang 74 Tập 1

Khám phá 2 trang 74 Toán 8 Tập 1: Cho tứ giác ABCD có các cạnh đối song song. Gọi O là giao điểm của hai đường chéo. Hãy chứng tỏ:

‒ Tam giác ABC bằng tam giác CDA.

‒ Tam giác OAB bằng tam giác OCD.

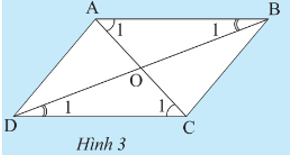
Lời giải:

• Tứ giác ABCD có AB // DC và AD // BC.

Từ AB // DC suy ra ${\widehat{A}}_1={\widehat{C}}_1$ (so le trong) và ${\widehat{B}}_1={\widehat{D}}_1$ (so le trong).

Từ AD // BC suy ra ${\widehat{A}}_2={\widehat{C}}_2$ (so le trong).

Xét DABC và DCDA có:

${\widehat{A}}_1={\widehat{C}}_1$; AC là cạnh chung; ${\widehat{A}}_2={\widehat{C}}_2$

Do đó DABC = DCDA (g.c.g).

• Do DABC = DCDA nên AB = CD (hai cạnh tương ứng).

Xét DOAB và DOCD có:

${\widehat{A}}_1={\widehat{C}}_1$; AB = CD; ${\widehat{B}}_1={\widehat{D}}_1$ (chứng minh trên)

Do đó DOAB = DOCD (g.c.g).

Thực hành 1 trang 74 Toán 8 Tập 1: Cho hình bình hành PQRS với I là giao điểm của hai đường chéo (Hình 4). Hãy chỉ ra các đoạn thẳng bằng nhau và các góc bằng nhau có trong hình.

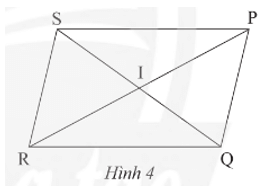
Lời giải:

Trong hình bình hành PQRS với I là giao điểm của hai đường chéo, ta có:

• Các đoạn thẳng bằng nhau: PQ = RS; PS = QR; IP = IR; IS = IQ.

• Các góc bằng nhau: $\widehat{PQR}=\widehat{PSR};\widehat{ SPQ}=\widehat{SRQ}; \widehat{RSQ}=\widehat{SQP}$;

$$\begin{gathered} \widehat{ PSQ}=\widehat{SQR};\widehat{ PRQ}=\widehat{RPS}; \widehat{PRS}=\widehat{RPQ}; \\ \widehat{ SIP}=\widehat{QIR}; \widehat{SIP}=\widehat{QIR};\widehat{ SIQ}=\widehat{PIR} \end{gathered}$$

Vận dụng 1 trang 74 Toán 8 Tập 1: Mắt lưới của một lưới bóng chuyền có dạng hình tứ giác có các cạnh đối song song. Cho biết độ dài hai cạnh của tứ giác này là 4 cm và 5 cm. Tìm độ dài hai cạnh còn lại.

Lời giải:

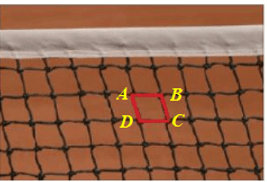
Giả sử mắt lưới của lưới bóng chuyền có dạng hình tứ giác ABCD có các cạnh đối song song và độ dài hai cạnh là 4 cm, 5 cm.

Tứ giác ABCD có các cạnh đối song song nên là hình bình hành. Giả sử AB = 4 cm, AD = 5 cm.

Do đó CD = AB = 4 cm; BC = AD = 5 cm.

Vận dụng 2 trang 74 Toán 8 Tập 1: Mặt trước của một công trình xây dựng được làm bằng kính có dạng hình bình hành EFGH với M là giao điểm của hai đường chéo (Hình 6). Cho biết EF = 40 m, EM = 36 m, HM = 16 m. Tính độ dài cạnh HG và độ dài hai đường chéo.

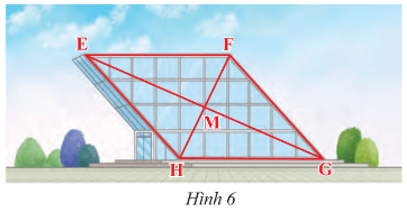
Lời giải:

EFGH là hình bình hành nên ta có:

• HG = EF = 40 m;

• M là trung điểm của EG nên EG = 2EM = 2.36 = 72 (m);

• M là trung điểm của FH nên FH = 2MH = 2.16 = 32 (m).

Vậy HG = 40 m và độ dài hai đường chéo lần lượt là EG = 72 m, FH = 32 m.

Khám phá 3 trang 75 Toán 8 Tập 1: Cho tứ giác ABCD có P là giao điểm của hai đường chéo. Giải thích tại sao AB // CD và AD // BC trong mỗi trường hợp sau:

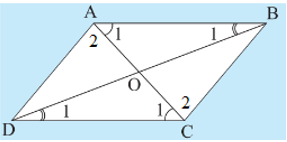
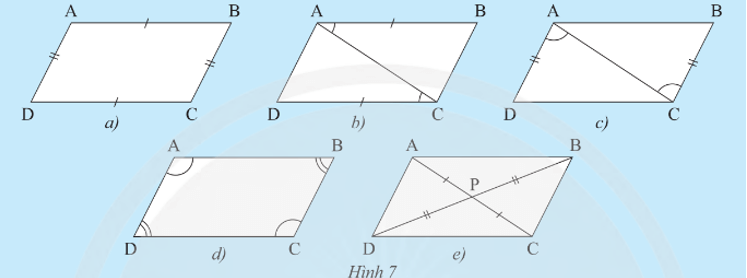
Trường hợp 1: AB = CD và AD = BC (Hình 7a).

Trường hợp 2: AB // CD và AB = CD (Hình 7b).

Trường hợp 3: AD // BC và AD = BC (Hình 7c).

Trường hợp 4: $\widehat{A}=\widehat{C},\widehat{B}=\widehat{D}$ (Hình 7d).

Trường hợp 5: PA = PC, PB = PD (Hình 7e).

Lời giải:

• Hình 7a):

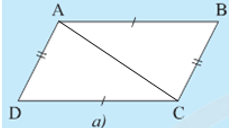
Xét DABC và DCDA có:

AB = CD; BC = DA; AC là cạnh chung

Do đó DABC = DCDA (c.c.c)

Suy ra $\widehat{BAC}=\widehat{DCA}$ và $\widehat{BCA}=\widehat{DAC}$ (các cặp góc tương ứng).

Vì $\widehat{BAC}=\widehat{DCA}$ và hai góc này ở vị trí so le trong nên AB // CD.

Vì $\widehat{BCA}=\widehat{DAC}$ và hai góc này ở vị trí so le trong nên AD // BC.

• Hình 7b):

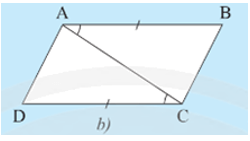
Ta có $\widehat{BAC}=\widehat{DCA}$ và hai góc này ở vị trí so le trong nên AB // CD.

Xét DABC và DCDA có:

AC là cạnh chung; $\widehat{BAC}=\widehat{DCA}$; AB = CD

Do đó DABC = DCDA (c.g.c)

Suy ra $\widehat{BCA}=\widehat{DAC}$ (hai góc tương ứng).

Mà hai góc này ở vị trí so le trong nên AD // BC.

• Hình 7c):

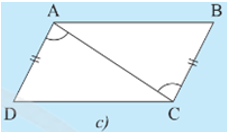
Ta có: $\widehat{BCA}=\widehat{DAC}$ và hai góc này ở vị trí so le trong nên AD // BC.

Xét DABC và DCDA có:

AC là cạnh chung; $\widehat{BCA}=\widehat{DAC}$; BC = AD

Do đó DABC = DCDA (c.g.c)

Suy ra $\widehat{BAC}=\widehat{DCA}$ (hai góc tương ứng).

Mà hai góc này ở vị trí so le trong nên AB // CD.

• Hình 7d):

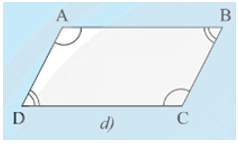
Xét tứ giác ABCD ta có $\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360°$ (định lí tổng các góc của một tứ giác)

Mà $\widehat{A}=\widehat{C},\widehat{B}=\widehat{D}$ nên ta có $\widehat{A}+\widehat{B}+\widehat{A}+\widehat{B}=360°$

Suy ra $\widehat{A}+\widehat{B}=\frac{360°}{2}=180°$ và $\widehat{A}+\widehat{D}=180°$

Do đó AD // BC và AB // CD.

• Hình 7e):

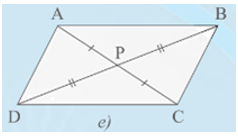
Xét DPAB và DPCD có:

PA = PC; $\widehat{APB}=\widehat{CPD}$ (đối đỉnh); PB = PD

Do đó DPAB = DPCD (c.g.c)

Suy ra $\widehat{BAP}=\widehat{DCP}$ (hai góc tương ứng)

Hay $\widehat{BAC}=\widehat{DCA}$, mà hai góc này ở vị trí so le trong nên AB // CD.

Tương tự ta cũng chứng minh được DPAD = DPCB (c.g.c)

Suy ra $\widehat{DAP}=\widehat{BCP}$ (hai góc tương ứng)

Hay $\widehat{DAC}=\widehat{BCA}$, mà hai góc này ở vị trí so le trong nên AD // BC.

Giải Toán 8 trang 76 Tập 1

Thực hành 2 trang 76 Toán 8 Tập 1: Trong các tứ giác ở Hình 9, tứ giác nào không là hình bình hành?

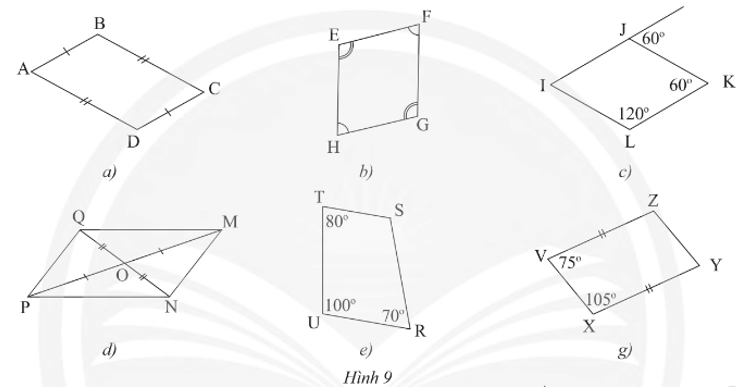
Lời giải:

• Hình 9a): Tứ giác ABCD có các cạnh đối bằng nhau nên là hình bình hành.

• Hình 9b): Tứ giác EFGH có các góc đối bằng nhau nên là hình bình hành.

• Hình 9c): Tứ giác IJKL có các cạnh đối song song nên là hình bình hành.

• Hình 9d): Tứ giác MNPQ có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên là hình bình hành.

• Hình 9e): Tứ giác RSTU có hai góc đối không bằng nhau nên không là hình bình hành.

• Hình 9g): Tứ giác VXYZ có hai cạnh đối VZ và XY vừa song song vừa bằng nhau nên là hình bình hành.

Vậy trong các tứ giác ở Hình 9, tứ giác RSTU không là hình bình hành.

Vận dụng 3 trang 76 Toán 8 Tập 1: Quan sát Hình 10, cho biết ABCD và AKCH đều là hình bình hành. Chứng minh ba đoạn thẳng AC, BD và HK có cùng trung điểm O.

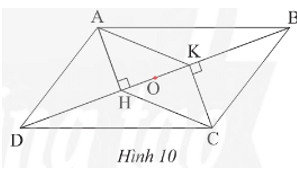
Lời giải:

Xét hình bình hành ABCD có hai đường chéo AC và BD cắt nhau tại trung điểm O của mỗi đường.

Xét hình bình hành AKCH có hai đường chéo AC và HK cắt nhau tại trung điểm O của mỗi đường.

Vậy ba đoạn thẳng AC, BD và HK có cùng trung điểm O.

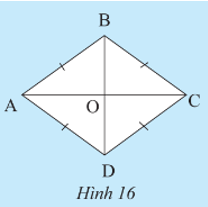
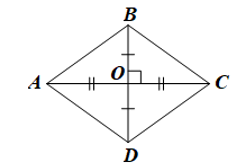
2. Hình thoi

Khám phá 4 trang 76 Toán 8 Tập 1: Hình 11a là hình chụp tấm lưới thép được đan thành nhiều mắt. Hình 11b là hình vẽ phóng to của một mắt lưới. Đo độ dài các cạnh của tứ giác ABCD và rút ra nhận xét.

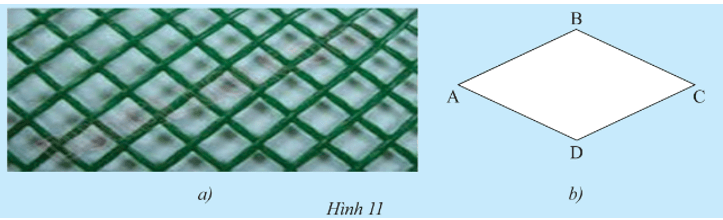
Lời giải:

Dùng thước đo độ dài ta xác định được AB = BC = CD = DA.

Khám phá 5 trang 77 Toán 8 Tập 1: a) Hình thoi có là hình bình hành không?

b) Cho hình thoi ABCD có O là giao điểm của hai đường chéo (Hình 13b). Các tam giác OAB, OCB, OCD, OAD có bằng nhau không?

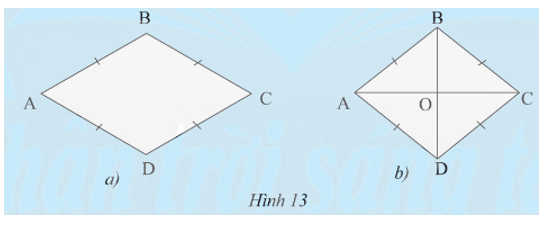
Lời giải:

a) Hình thoi có 4 cạnh bằng nhau AB = BC = CD = DA

Suy ra các cạnh đối cũng bằng nhau: AB = CD và AD = BC.

Do đó hình thoi cũng là hình bình hành.

b) Theo câu a, hình thoi ABCD cũng là hình bình hành.

Khi đó hai đường chéo AC và BD cắt nhau tại trung điểm của mỗi đường.

Hay OA = OC và OB = OD.

Xét DOAB và DOAD có:

OA là cạnh chung; OB = OD; AB = AD

Do đó DOAB = DOAD (c.c.c)    (1)

Chứng minh tương tự ta cũng có DOCB = DOCD (c.c.c)   (2)

Xét DOAB và DOCD có:

OA = OC; $\widehat{AOB}=\widehat{COD}$ (đối đỉnh); OB = OD

Do đó DOAB = DOCD (c.g.c)    (3)

Từ (1), (2) và (3) ta có: DOAB = DOAD = DOCD = DOCB.

Giải Toán 8 trang 78 Tập 1

Thực hành 3 trang 78 Toán 8 Tập 1: Cho hình thoi MNPQ có I là giao điểm của hai đường chéo.

a) Tính MP khi biết MN = 10 dm, IN = 6 dm.

b) Tính $\widehat{IMN}$ khi biết $\widehat{MNP}=128°$.   

Lời giải:

a)

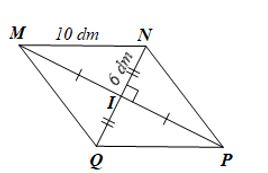
Do MNPQ là hình thoi nên hai đường chéo MP và NQ vuông góc với nhau tại trung điểm của mỗi đường.

Áp dụng định lí Pythagore vào DMNI vuông tại I, ta có:

MN² = MI² + NI²

Suy ra $MI=\sqrt{M{N}^2-N{I}^2}=\sqrt{{10}^2-6^2}=8$ (dm).

Do I là trung điểm của MP nên MP = 2MI = 2.8 = 16 (dm).

Vậy MP = 16 dm.

b)

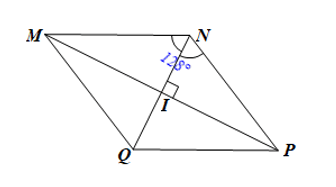
Vì MNPQ là hình thoi nên MQ // NP

Do đó $\widehat{MNP}+\widehat{NMQ}=180°$

Suy ra $\widehat{NMQ}=180°-\widehat{MNP}=180°-128°=52°$.

Do MNPQ là hình thoi nên MP và tia phân giác của góc NMQ.

Suy ra $\widehat{IMN}=\frac{1}{2}\widehat{NMQ}=\frac{1}{2}.52°=26°$.

Vậy $\widehat{IMN}=26°$.

Vận dụng 4 trang 78 Toán 8 Tập 1: Tính độ dài cạnh của các khuy áo hình thoi có độ dài hai đường chéo lần lượt là 3,2 cm và 2,4 cm.

Lời giải:

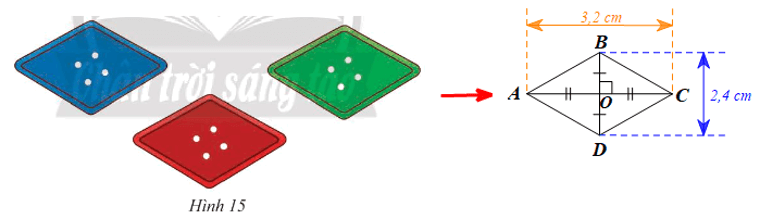
Hình ảnh chiếc khuy áo được vẽ lại bởi hình thoi ABCD như hình vẽ trên.

Gọi O là giao điểm của hai đường chéo AC và BD.

Khi đó hai đường chéo AC và BD vuông góc với nhau tại trung điểm O của mỗi đường.

Suy ra OA = $\frac{1}{2}$AC = 1,6 cm và OB = $\frac{1}{2}$BD = 1,2 cm.

Áp dụng định lí Pythagore vào DOAB vuông tại O, ta có:

AB² = OA² + OB²

Suy ra $AB=\sqrt{O{A}^2+O{B}^2}=\sqrt{1,6^2+1,2^2}=2$ (cm).

Vậy độ dài cạnh của khuy áo là 2 cm.

Khám phá 6 trang 78 Toán 8 Tập 1: Cho ABCD là một hình bình hành. Giải thích tại sao tứ giác ABCD có bốn cạnh bằng nhau trong mỗi trường hợp sau:

Trường hợp 1: AB = AD.

Trường hợp 2: AC vuông góc với BD.

Trường hợp 3: AC là phân giác góc BAD.

Trường hợp 4: BD là phân giác góc ABC.

Lời giải:

• Trường hợp 1: AB = AD.

Vì ABCD là hình bình hành nên AD = BC và AB = CD.

Lại có AB = AD (giả thiết)

Do đó AB = AD = BC = CD.

• Trường hợp 2: AC vuông góc với BD.

Vì ABCD là hình bình hành nên AD = BC, AB = CD và hai đường chéo AC, BD cắt nhau tại trung điểm O của mỗi đường.

Xét DOAB và DOCB có:

$\widehat{AOB}=\widehat{COB}=90°$; OB là cạnh chung; OA = OC

Do đó DOAB = DOCB (hai cạnh góc vuông)

Suy ra AB = CB (hai cạnh tương ứng).

Mà AD = BC và AB = CD nên AB = CD = CB = DA.

• Trường hợp 3: AC là phân giác góc BAD.

Vì ABCD là hình bình hành nên AB // CD

Do đó $\widehat{BAC}=\widehat{CDA}$ (so le trong).

Mà $\widehat{BAC}=\widehat{CAD}$ (do AC là tia phân giác của góc BAD)

Suy ra $\widehat{CAD}=\widehat{CDA}$.

Tam giác ACD có $\widehat{CAD}=\widehat{CDA}$ nên là tam giác cân tại D

Suy ra DA = DC.

Lại có AB = CD và AD = BC (chứng minh trên).

Do đó AB = BC = CD = DA.

• Trường hợp 4: BD là phân giác góc ABC.

Chứng minh tương tự như trường hợp 3 ta cũng có AB = BC = CD = DA.

Giải Toán 8 trang 79 Tập 1

Vận dụng 5 trang 79 Toán 8 Tập 1: Một hoa văn trang trí được ghép bởi ba hình tứ giác có độ dài mỗi cạnh đều bằng 2 cm (Hình 18). Gọi tên các tứ giác này và tính chu vi của hoa văn.

Lời giải:

Tứ giác có độ dài mỗi cạnh đều bằng 2 cm nên tứ giác này là hình thoi.

Chu vi của một hình thoi là: 4.2 = 8 (cm).

Chu vi của hoa văn là: 3.8 = 24 (cm).

Vận dụng 6 trang 79 Toán 8 Tập 1: Một tứ giác có chu vi là 52 cm và một đường chéo là 24 cm. Tìm độ dài của mỗi cạnh và đường chéo còn lại nếu biết hai đường chéo vuông góc tại trung điểm của mỗi đường.

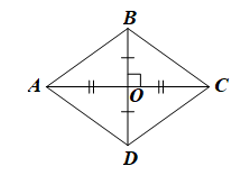
Lời giải:

Tứ giác ABCD có hai đường chéo vuông góc tại trung điểm của mỗi đường nên là hình thoi.

Độ dài cạnh của hình thoi ABCD là: 52 : 4 = 13 (cm).

Giả sử đường chéo AC = 24 cm và O là giao điểm hai đường chéo.

Ta có O là trung điểm của AC nên OA = $\frac{1}{2}$AC = 12 cm.

Áp dụng định lí Pythagore vào DOAB vuông tại O, ta có:

AB² = OA² + OB²

Suy ra $OB=\sqrt{A{B}^2-O{A}^2}=\sqrt{{13}^2-{12}^2}=5$ (cm).

Do O là trung điểm của BD nên BD = 2OB = 2.5 = 10 (cm).

Vậy hình thoi có độ dài cạnh là 13 cm và độ dài đường chéo còn lại là 10 cm.

Bài tập

Giải Toán 8 trang 80 Tập 1

Bài 1 trang 80 Toán 8 Tập 1: Cần thêm một điều kiện gì để mỗi tứ giác trong Hình 19 trở thành hình bình hành?

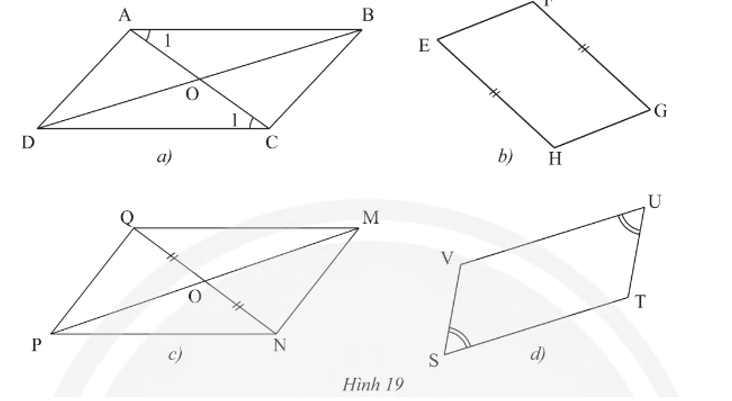
Lời giải:

• Hình 19a):

Ta có ${\widehat{A}}_1={\widehat{C}}_1$ và hai góc này ở vị trí so le trong nên AB // CD.

Để tứ giác ABCD là hình bình hành thì có hai trường hợp sau:

+) Trường hợp 1: Tứ giác ABCD có hai cặp cạnh đối song song. Do đó cần thêm điều kiện AD // BC.

+) Trường hợp 2: Tứ giác ABCD có cặp cạnh đối vừa song song, vừa bằng nhau. Do đó cần thêm điều kiện AB = CD.

• Hình 19b): Tứ giác EFGH đã có một cặp cạnh đối bằng nhau (EH = GF).

Để tứ giác EFGH là hình bình hành thì có hai trường hợp sau:

+) Trường hợp 1: Tứ giác EFGH có hai cặp cạnh đối bằng nhau. Do đó cần thêm điều kiện EF = GH.

+) Trường hợp 2: Tứ giác EFGH có cặp cạnh đối vừa song song, vừa bằng nhau. Do đó cần thêm điều kiện EH // GF.

• Hình 19c):

Ta có OQ = ON nên O là trung điểm của NQ.

Để tứ giác MNPQ là hình bình hành thì tứ giác MNPQ có hai đường chéo cắt nhau tại trung điểm của mỗi đường. Do đó cần thêm điều kiện O là trung điểm của MP.

• Hình 19d): Tứ giác STUV đã có một cặp góc đối bằng nhau $\left(\widehat{S}=\widehat{U}\right)$.

Để tứ giác STUV là hình bình hành thì tứ giác STUV có cac cặp góc đối bằng nhau. Do đó cần thêm điều kiện $\left(\widehat{T}=\widehat{V}\right)$.

Bài 2 trang 80 Toán 8 Tập 1: Cho hình bình hành ABCD, kẻ AH vuông góc với BD tại H và CK vuông góc với BD tại K (Hình 20).

a) Chứng minh tứ giác AHCK là hình bình hành.

b) Gọi I là trung điểm của HK. Chứng minh IB = ID.

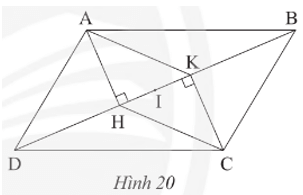
Lời giải:

a) Do ABCD là hình bình hành nên AD // BC và AD = BC.

Do AD // BC nên $\widehat{ADB}=\widehat{CBD}$ (so le trong)

Xét DADH và DCBK có:

$\widehat{AHD}=\widehat{CKB}=90°$;

AD = BC (chứng minh trên);

$\widehat{ADH}=\widehat{CBK}$ (do $\widehat{ADB}=\widehat{CBD}$).

Do đó DADH = DCBK (cạnh huyền – góc nhọn).

Suy ra AH = CK (hai cạnh tương ứng).

Ta có AH ⊥ DB và CK  ⊥ DB nên AH // CK.

Tứ giác AHCK có AH // CK và AH = CK nên AHCK là hình bình hành (dấu hiệu nhận biết).

b) Do AHCK là hình bình hành (câu a) nên hai đường chéo AC và HK cắt nhau tại trung điểm của mỗi đường.

Mà I là trung điểm của HK (giả thiết) nên I là trung điểm của AC.

Do ABCD là hình bình hành nên hai đường chéo AC và BD cắt nhau tại trung điểm của mỗi đường.

Mà I là trung điểm của AC nên I là trung điểm của BD, hay IB = ID.

Bài 3 trang 80 Toán 8 Tập 1: Cho hình bình hành ABCD. Gọi E là trung điểm của AD, F là trung điểm của BC.

a) Chứng minh rằng tứ giác EBFD là hình bình hành.

b) Gọi O là giao điểm của hai đường chéo của hình bình hành ABCD. Chứng minh rằng ba điểm E, O, F thẳng hàng.

Lời giải:

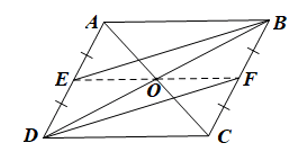
a) ABCD là hình bình hành nên AD = BC và AD // BC.

Mà E là trung điểm của AD nên AE = ED;

       F là trung điểm của BC nên BF = FC.

Suy ra DE = BF.

Xét tứ giác EBFD có DE // BF (do AD // BC) và DE = BF nên là hình bình hành (dấu hiệu nhận biết).

b) Ta có O là giao điểm của hai đường chéo của hình bình hành ABCD nên O là trung điểm của BD.

Do EBFD là hình bình hành nên hai đường chéo BD và EF cắt nhau tại trung điểm của mỗi đường.

Mà O là trung điểm của BD nên O là trung điểm của EF.

Vậy ba điểm E, O, F thẳng hàng.

Bài 4 trang 80 Toán 8 Tập 1: Cho hình bình hành ABCD (AB > BC). Tia phân giác của góc D cắt AB tại E, tia phân giác của góc B cắt CD tại F.

a) Chứng minh DE // BF.

b) Tứ giác DEBF là hình gì?

Lời giải:

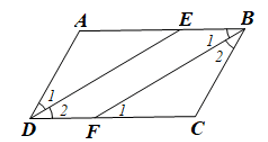
a) Do ABCD là hình bình hành nên AB // CD và .

Vì DE là tia phân giác của góc D nên ${\widehat{D}}_1={\widehat{D}}_2=\frac{1}{2}\widehat{D}$.

Vì BF là tia phân giác của góc B nên ${\widehat{B}}_1={\widehat{B}}_2=\frac{1}{2}\widehat{B}$.

Do đó ${\widehat{B}}_1={\widehat{D}}_2$.

Do AB // CD nên ${\widehat{B}}_1={\widehat{F}}_1$ (so le trong).

Suy ra ${\widehat{D}}_2={\widehat{F}}_1$

Mà hai góc này ở vị trí so le trong nên DE // BF.

b) Tứ giác DEBF có EB // FD (do AB // CD) và DE // BF nên là hình bình hành (dấu hiệu nhận biết).

Bài 5 trang 80 Toán 8 Tập 1: Cho hình bình hành ABCD. Gọi I và K lần lượt là trung điểm của các cạnh AB và CD; E và F lần lượt là giao điểm của AK và CI với BD.

a) Chứng minh tứ giác AEFI là hình thang.

b) Chứng minh DE = EF = FB.

Lời giải:

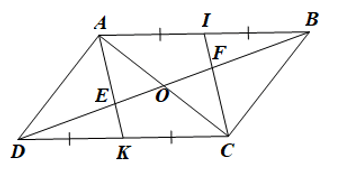
a) Do ABCD là hình bình hành nên AB = CD và AB // CD.

Vì I là trung điểm của AB nên $AI=IB=\frac{1}{2}AB$.

Vì K là trung điểm của CD nên $CK=DK=\frac{1}{2}CD$.

Do đó AI = CK.

Tứ giác AICK có AI // CK (do AB // CD) và AI = CK nên là hình bình hành (dấu hiệu nhận biết).

Suy ra AK // CI hay AE // IF.

Tứ giác AEFI có AE // IF nên là hình thang.

b) Gọi O là giao điểm của hai đường chéo hình bình hành ABCD.

Do đó O là trung điểm của AC và BD.

Xét DABC có BO, CI là hai đường trung tuyến của tam giác và BO, CI cắt nhau tại F nên F là trọng tâm của DABC.

Suy ra $BF=\frac{2}{3}BO$ và $FO=\frac{1}{3}BO$.

Chứng minh tương tự đối với DACD ta cũng có E là trọng tâm của DACD.

Suy ra $DE=\frac{2}{3}DO$ và $EO=\frac{1}{3}DO$.

Lại có O là trung điểm BD nên BO = DO.

Do đó $BF=DE=\frac{2}{3}BO$ và $FO=EO=\frac{1}{3}BO$

Mặt khác $EF=EO+FO=\frac{1}{3}BO+\frac{1}{3}BO=\frac{2}{3}BO$.

Suy ra $DE=EF=FB=\frac{2}{3}BO$.

Vậy DE = EF = FB.

Giải Toán 8 trang 81 Tập 1

Bài 6 trang 81 Toán 8 Tập 1: Quan sát Hình 21. Chứng minh rằng tứ giác EFGH là hình thoi.

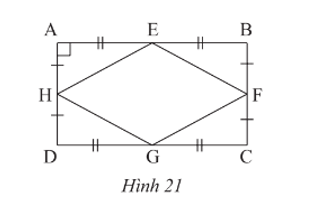
Lời giải:

Ta có AE = EB nên AB = 2AE.

         DG = GC nên DC = 2DG.

Mà AE = DG nên AB = DC.

Chứng minh tương tự ta cũng có: AD = BC.

Tứ giác ABCD có AB = DC và AD = BC nên là hình bình hành (dấu hiệu nhận biết).

Suy ra AB // CD và AD // BC.

Lại có AD ⊥ AB nên AD ⊥ CD; AB ⊥ BC; BC ⊥ CD.

Xét DAEH và DBEF có:

$\widehat{EAH}=\widehat{EBF}=90°$; AE = BE; AH = BF.

Do đó DAEH = DBEF (hai cạnh góc vuông).

Suy ra HE = FE (hai cạnh tương ứng).

Chứng minh tương tự ta cũng có: HE = HG; HE = FG.

Do đó HE = EF = FG = GH.

Tứ giác EFGH có HE = EF = FG = GH nên là hình thoi.

Bài 7 trang 81 Toán 8 Tập 1: Cho hình thoi ABCD, hai đường chéo AC và BD cắt nhau tại O. Biết AC = 6 cm, BD = 8 cm. Tính độ dài cạnh của hình thoi ABCD.

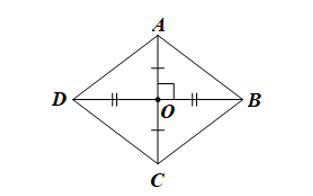
Lời giải:

Do ABCD là hình thoi nên hai đường chéo AC và BD cắt nhau tại trung điểm O của mỗi đường.

Do đó $OA=\frac{1}{2}AC=3\left(cm\right)$ và $OB=\frac{1}{2}BD=4\left(cm\right)$.

Áp dụng định lí Pythagore vào DOAB vuông tại O, ta có:

AB² = OA² + OB²

Suy ra $AB=\sqrt{O{A}^2+O{B}^2}=\sqrt{3^2+4^2}=5\left(cm\right)$.

Bài 8 trang 81 Toán 8 Tập 1: Cho tam giác ABC cân tại A, gọi M là trung điểm của BC. Lấy điểm D đối xứng với điểm A qua BC.

a) Chứng minh tứ giác ABDC là hình thoi.

b) Gọi E, F lần lượt là trung điểm của AB và AC, lấy điểm O sao cho E là trung điểm của OM. Chứng minh hai tam giác AOB và MBO vuông và bằng nhau.

c) Chứng minh tứ giác AEMF là hình thoi.

Lời giải:

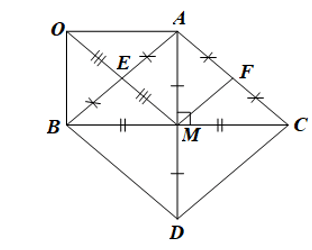
a) Ta có D đối xứng với A qua BC nên M là trung điểm của AD và AD ⊥ BC.

Tứ giác ABDC có hai đường chéo AD và BD cắt nhau tại trung điểm của mỗi đường nên là hình bình hành.

Lại có hai đường chéo AD ⊥ BC nên hình bình hành ABDC là hình thoi.

b) Ta có E là trung điểm của AB và OM nên hai đường chéo của tứ giác OAMB cắt nhau tại trung điểm của mỗi đường.

Do đó tứ giác OAMB là hình bình hành.

Suy ra OA // BM và OB // AM.

Ta có OB // AM và AM ⊥ BM nên OB ⊥ BM, do đó DMBO vuông tại B.

Ta có OA // BM và OB ⊥ BM nên OA ⊥ OB, do đó DAOB vuông tại O.

Do OAMB là hình bình hành nên OA = BM và OB = AM.

Xét DMBO vuông tại B và DAOB vuông tại O có:

OB = AM; BM = OA

Do đó DMBO = DAOB (hai cạnh góc vuông).

Bài 9 trang 81 Toán 8 Tập 1: Tìm các hình bình hành và hình thang có trong Hình 22.

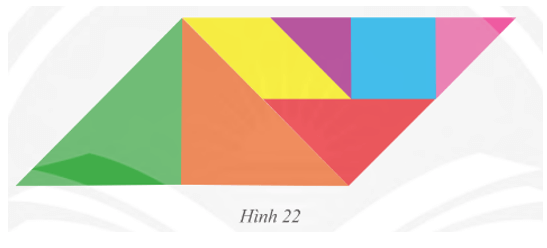
Lời giải:

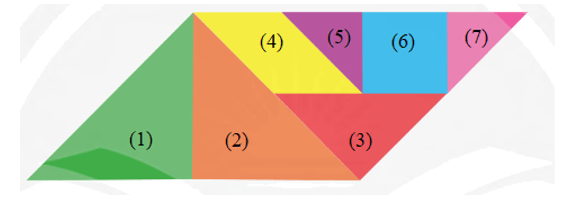
Giả sử Hình 22 được ghép bởi các hình (1), (2), (3), (4), (5), (6) và (7) như hình vẽ trên.

‒ Trong Hình 22 có các hình bình hành:

• Hình (4);

• Hình (6);

• Hình ghép bởi các hình (1), (2), (3), (4), (5), (6) và (7).

‒ Trong Hình 22 có các hình thang:

• Bao gồm các hình bình hành kể trên;

• Hình ghép bởi các hình (2), (3), (4), (5), (6) và (7);

• Hình ghép bởi các hình (4), (5), (6) và (7);

• Hình ghép bởi các hình (4), (5) và (6);

• Hình ghép bởi các hình (5), (6) và (7);

• Hình ghép bởi các hình (4) và (5);

• Hình ghép bởi các hình (5) và (6);

• Hình ghép bởi các hình (6) và (7).

Xem thêm các bài giải SGK Toán lớp 8 Chân trời sáng tạo hay, chi tiết khác:

Bài 2: Tứ giác

Bài 3: Hình thang – Hình thang cân

Bài 5: Hình chữ nhật – Hình vuông

Bài tập cuối chương 3