Với giải SGK Toán 8 Chân trời sáng tạo trang 25 chi tiết trong Bài 4: Phân tích đa thức thành nhân tử giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 8. Mời các bạn đón xem:

Giải Toán 8 trang 25 Tập 1 (Chân trời sáng tạo)

Thực hành 3 trang 25 Toán 8 Tập 1: Phân tích các đa thức sau thành nhân tử:

a) a³ – a²b + a – b;

b) x² – y² + 2y – 1.

Lời giải:

a) a³ – a²b + a – b

= (a³ – a²b) + (a – b)

= a²(a – b) + (a – b)

= (a – b)(a² + 1).

b) x² – y² + 2y – 1

= x² – (y² – 2y + 1)

= x² – (y – 1)²

= (x + y – 1).[x – (y – 1)]

= (x + y – 1)(x – y + 1).

Vận dụng 3 trang 25 Toán 8 Tập 1: Có thể ghép bốn tấm pin mặt trời với kích thước như Hình 2 thành một hình chữ nhật không? Nếu có, tính độ dài các cạnh và diện tích hình chữ nhật đó. Biết a = 0,8; b = 2 (các kích thước tính theo mét).

Lời giải:

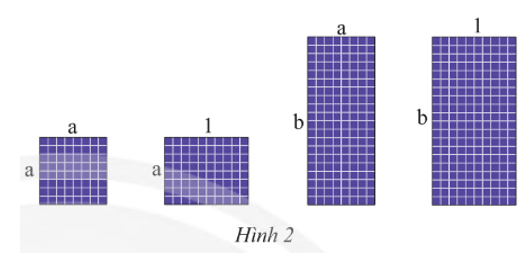
Diện tích tấm pin hình vuông có cạnh bằng a là: a² (m²).

Diện tích tấm pin hình chữ nhật có chiều dài bằng 1 và chiều rộng bằng a là: a.1 = a (m²).

Diện tích tấm pin hình chữ nhật có chiều dài bằng b và chiều rộng bằng a là: ab (m²).

Diện tích tấm pin hình chữ nhật có chiều dài bằng b và chiều rộng bằng 1 là: b.1 = b (m²).

Tổng diện tích bốn tấm pin mặt trời là:

S = a² + a + ab + b = (a² + a) + (ab + b)

                               = a(a + 1) + b(a + 1)

                               = (a + 1)(a + b) (m²).

Vậy có thể ghép bốn tấm pin mặt trời với kích thước như Hình 2 thành một hình chữ nhật có chiều rộng là a + 1 (m) và chiều dài là a + b (m).

Với a = 0,8 (m) và b = 2 (m) ta có:

• Chiều rộng hình chữ nhật đó là 0,8 + 1 = 1,8 (m).

• Chiều dài hình chữ nhật đó là 0,8 + 2 = 2,8 (m).

• Diện tích hình chữ nhật đó là: 1,8 . 2,8 = 5,04 (m²).

Bài tập

Bài 1 trang 25 Toán 8 Tập 1: Phân tích các đa thức sau thành nhân tử:

a) x³ + 4x;

b) 6ab – 9ab²;

c) 2a(x – 1) + 3b(1 – x);

d) (x – y)² – x(y – x).

Lời giải:

a) x³ + 4x = x.x² + x.4 = x(x² + 4).

b) 6ab – 9ab² = 3ab.2 – 3ab.3b = 3ab(2 – 3b).

c) 2a(x – 1) + 3b(1 – x)

= 2a(x – 1) + 3b[– (x – 1)]

= 2a(x – 1) – 3b(x – 1)

= (x – 1)(2a – 3b).

d) (x – y)² – x(y – x)

= (x – y)² + x(x – y)

= (x – y)(x – y + x)

= (x – y)(2x – y).

Bài 2 trang 25 Toán 8 Tập 1: Phân tích các đa thức sau thành nhân tử:

a) 4x² – 1;

b) (x + 2)² – 9;

c) (a + b)² – (a – 2b)².

Lời giải:

a) 4x² – 1 = (2x)² – 1² = (2x + 1)(2x –1).

b) (x + 2)² – 9 = (x + 2)² – 3²

                       = (x + 2 + 3)(x + 2 – 3)

                       = (x + 5)(x – 1).

c) (a + b)² – (a – 2b)²

= [(a + b) + (a – 2b)] . [(a + b) – (a – 2b)]

= [a + b + a – 2b] . [a + b – a + 2b]

= (2a – b).3b.

Bài 3 trang 25 Toán 8 Tập 1: Phân tích các đa thức sau thành nhân tử:

a) 4a² + 4a + 1;

b) –3x² + 6xy – 3y²;

c) (x + y)² – 2(x + y)z + z².

Lời giải:

a) 4a² + 4a + 1

= (2a)² + 2.2a.1 + 1²

= (2a + 1)².

b) –3x² + 6xy – 3y²

= –3(x² – 2xy + y²)

= –3(x – y)².

c) (x + y)² – 2(x + y)z + z²

= [(x + y) – z]²

= (x + y – z)².

Bài 4 trang 25 Toán 8 Tập 1: Phân tích các đa thức sau thành nhân tử:

a) 8x³ – 1;

b) x³ + 27y³;

c) x³ – y⁶.

Lời giải:

a) 8x³ – 1

= (2x)³ – 1³

= (2x – 1)[(2x)² + 2x.1 + 1²]

= (2x – 1)(4x² + 2x + 1).

b) x³ + 27y³

= x³ + (3y)³

= (x + 3y)[x² – x.3y + (3y)²]

= (x + 3y)(x² – 3xy + 9y²).

c) x³ – y⁶

= x³ – (y²)³

= (x – y²)[x² + x.y² + (y²)²]

= (x – y²)(x² + xy² + y⁴).

Bài 5 trang 25 Toán 8 Tập 1: Phân tích các đa thức sau thành nhân tử:

a) 4x³ – 16x;

b) x⁴ – y⁴;

c) xy² + x²y + $\frac{1}{4}$y³;

d) x² + 2x – y² + 1.

Lời giải:

a) 4x³ – 16x

= 4x(x² – 4)

= 4x(x² – 2²)

= 4x(x + 2)(x – 2).

b) x⁴ – y⁴

= (x²)² – (y²)²

= (x² + y²)(x² – y²)

= (x² + y²)(x + y)(x – y).

c) xy² + x²y + $\frac{1}{4}$y³

= y(xy + x² + $\frac{1}{4}$y²)

$=y\left[x^2+2.x.\frac{1}{2}y+{\left(\frac{1}{2}y\right)}^2\right]$

$=y{\left(x+\frac{1}{2}y\right)}^2$.

d) x² + 2x – y² + 1

= (x² + 2x + 1) – y²

= (x + 1)² – y²

= (x + 1 + y)(x + 1 – y).

Bài 6 trang 25 Toán 8 Tập 1: Phân tích các đa thức sau thành nhân tử:

a) x² – xy + x – y;

b) x² + 2xy – 4x – 8y;

c) x³ – x² – x + 1.

Lời giải:

a) x² – xy + x – y

= (x² – xy) + (x – y)

= x(x – y) + (x – y)

= (x – y)(x + 1).

b) x² + 2xy – 4x – 8y

= (x² + 2xy) – (4x + 8y)

= x(x +  2y) – 4(x + 2y)

= (x +  2y)(x – 4).

c) x³ – x² – x + 1

= (x³ – x²) – (x – 1)

= x²(x – 1) – (x – 1)

= (x – 1)(x² – 1)

= (x – 1)(x + 1)(x – 1)

= (x – 1)²(x + 1).

Bài 7 trang 25 Toán 8 Tập 1: Cho y > 0. Tìm độ dài cạnh của hình vuông có diện tích bằng 49y² + 28y + 4.

Lời giải:

Giả sử hình vuông có độ dài cạnh bằng a (a > 0), khi đó diện tích của hình vuông là a².

Tức là 49y² + 28y + 4 = a².

Ta phân tích đa thức 49y² + 28y + 4 thành nhân tử có dạng a².

49y² + 28y + 4

= (7y)² + 2.7y.2 + 2²

= (7y + 2)²

Vậy độ dài cạnh của hình vuông có diện tích bằng 49y² + 28y + 4 là 7y + 2.