Với giải SGK Toán 8 Chân trời sáng tạo trang 87 chi tiết trong Bài 5: Hình chữ nhật – Hình vuông giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 8. Mời các bạn đón xem:

Giải Toán 8 trang 87 Tập 1 (Chân trời sáng tạo)

Bài tập

Bài 1 trang 87 Toán 8 Tập 1: Cho Hình 14. Tìm x.

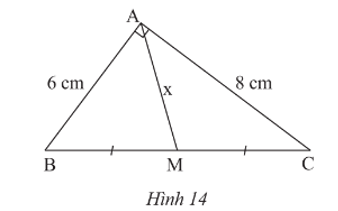
Lời giải:

Áp dụng định lí Pythagore vào DABC vuông tại A, ta có:

BC² = AB² + AC² = 6² + 8² = 100 = 10²

Suy ra BC = 10 (cm).

Xét DABC vuông tại A có AM là đường trung tuyến ứng với cạnh huyền nên AM bằng nửa cạnh huyền BC.

Do đó $x=AM=\frac{1}{2}BC=\frac{1}{2}.10=5\left(cm\right)$.

Vậy x = 5 cm.

Bài 2 trang 87 Toán 8 Tập 1: Cho Hình 15. Vẽ thêm điểm P để tứ giác MNPQ là hình chữ nhật.

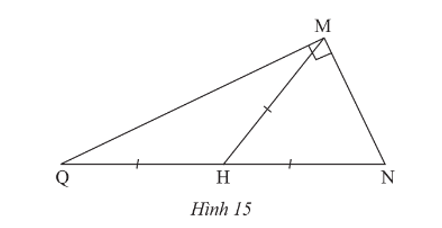
Lời giải:

Lấy điểm P sao cho H là trung điểm của MP (hình vẽ).

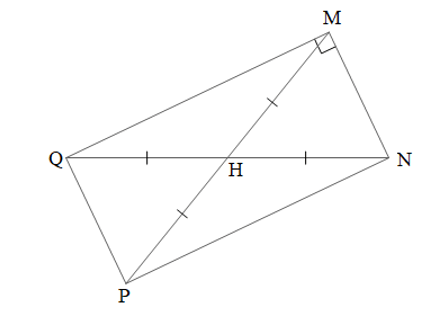
Giải thích cách vẽ:

Tứ giác MNPQ có H là trung điểm của hai đường chéo MP và NQ nên là hình bình hành.

Lại có $\widehat{NMQ}=90°$ nên hình bình hành MNPQ là hình chữ nhật.

Bài 3 trang 87 Toán 8 Tập 1: Cho tam giác ABC có đường cao AH. Gọi I là trung điểm của AC, E là điểm đối xứng với H qua I. Gọi M, N lần lượt là trung điểm của HC, CE. Các đường thẳng AM, AN cắt HE tại G và K.

a) Chứng minh tứ giác AHCE là hình chữ nhật.

b) Chứng minh HG = GK = KE.

Lời giải:

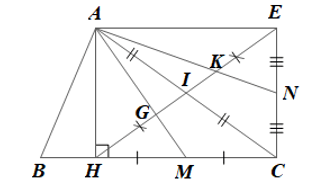
a) Do E là điểm đối xứng với H qua I nên I là trung điểm của HE.

Tứ giác AHCE có hai đường chéo AC và HE cắt nhau tại trung điểm I của mỗi đường nên là hình bình hành.

Lại có $\widehat{AHC}=90°$ nên hình bình hành AHCE là hình chữ nhật.

b) Xét DAHC có AM, HI là hai đường trung tuyến cắt nhau tại G nên G là trọng tâm của DAHC.

Suy ra $HG=\frac{2}{3}HI$ và $IG=\frac{1}{2}HG$.

Chứng minh tương tự đối với DAEC có K là trọng tâm của  DAEC.

Suy ra $EK=\frac{2}{3}EI$ và $IK=\frac{1}{2}EK$.

Ta có: $HG=\frac{2}{3}HI$, $EK=\frac{2}{3}EI$ và HI = EI nên $HG=EK\left(=\frac{2}{3}EI\right)$.

Lại có: $IG=\frac{1}{2}HG$ và $IK=\frac{1}{2}EK$ nên $IG=IK=\frac{1}{2}HG$

Mặt khác $GK=IG+IK=\frac{1}{2}HG+\frac{1}{2}HG=HG$.

Vậy HG = GK = KE.

Bài 4 trang 87 Toán 8 Tập 1: Cho tam giác ABC vuông tại A (AB < AC). Gọi D là trung điểm của BC. Vẽ DE // AB, vẽ DF // AC (E ∈ AC, F ∈ AB). Chứng minh rằng:

a) Tứ giác AEDF là hình chữ nhật.

b) Tứ giác BFED là hình bình hành.

Lời giải:

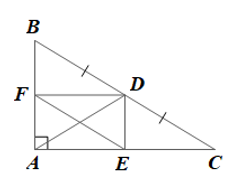
a) Tam giác ABC vuông tại A nên $\widehat{BAC}=90°$ hay AB ⊥ AC.

Do DE // AB và AB ⊥ AC nên DE ⊥ AC hay $\widehat{DEA}=90°$.

Do DF // AC và AB ⊥ AC nên DF ⊥ AB hay $\widehat{DFA}=90$

Tứ giác AEDF có $\widehat{BAC}=90°$, $\widehat{DEA}=90°$ và $\widehat{DFA}=90$ nên là hình chữ nhật.

b) Do AEDF là hình chữ nhật nên AF = ED và AD = EF (tính chất hình chữ nhật).

Xét DABC có AD là đường trung tuyến ứng với cạnh huyền BC nên bằng nửa cạnh huyền BC, do đó $AD=DB=DC=\frac{1}{2}BC$.

Từ đó suy ra $AD=EF=DB=DC=\frac{1}{2}BC$

Xét DBDF và DEFD có:

$\widehat{BFD}=\widehat{EDF}=90°$;

BD = EF (chứng minh trên);

DF là cạnh chung.

Do đó DBDF = DEFD (cạnh huyền – cạnh góc vuông).

Suy ra FB = DE (hai cạnh tương ứng).

Xét tứ giác BFED có FB = DE và FB // DE (do AB // DE) nên là hình bình hành.

Bài 5 trang 87 Toán 8 Tập 1: Lấy một tờ giấy, gấp làm tư để có một góc vuông như trong Hình 16, dùng kéo cắt theo đường MN sao cho OM = ON. Mở phần giấy cắt được ra ta được một tứ giác.

Tứ giác đó là hình gì? Giải thích kết luận của em.

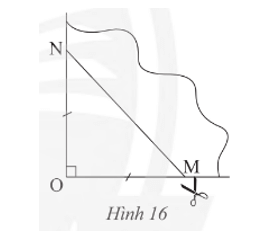
Lời giải:

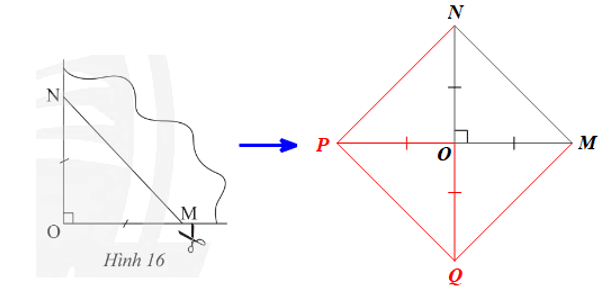
Mở phần giấy cắt được ra ta được một tứ giác MNPQ như hình vẽ trên.

Ta có OM = ON = OP = OQ nên:

• O là trung điểm của MP và NQ;

• MP = OM + OP = 2OM và NQ = ON + OQ = 2ON

Suy ra MP = NQ.

Xét tứ giác MNPQ có hai đường chéo MP và NQ cắt nhau tại trung điểm O của mỗi đường nên là hình bình hành.

Lại có hai đường chéo bằng nhau MP = NQ nên là hình chữ nhật.

Mặt khác MP ⊥ NQ nên hình chữ nhật MNPQ có hai đường chéo vuông góc với nhau.

Do đó MNPQ là hình vuông.