Toptailieu.vn biên soạn và giới thiệu Chuyên đề Giá trị lớn nhất và giá trị nhỏ nhất của hàm số gồm đầy đủ các phần: Lý thuyết, phương pháp giải, bài tập minh họa có lời giải chi tiết giúp học sinh làm tốt bài tập Toán 12 từ đó học tốt môn Toán. Mời các bạn đón xem:

Giá trị lớn nhất và giá trị nhỏ nhất của hàm số: Lý thuyết, cách giải và bài tập hay, chi tiết

A. Lý thuyết

I. Định nghĩa

Cho hàm số y = f(x) xác định trên tập D.

a) Số M được gọi là giá trị lớn nhất của hàm số y = f(x) trên tập D nếu $f\left(x\right)\le M$ với mọi x thuộc D và tồn tại x₀$\in$D sao cho f(x₀) = M.

Kí hiệu: $M=\underset{D}{max}f\left(x\right)$

b) Số m được gọi là giá trị nhỏ nhất của hàm số y = f(x) trên tập D nếu $f\left(x\right)\ge m$ với mọi x thuộc D và tồn tại x₀$\in$D sao cho f(x₀) = m.

Kí hiệu: $m=\underset{D}{\min }f\left(x\right)$.

- Ví dụ 1. Cho hàm số y = f(x) có bảng biến thiên như sau:

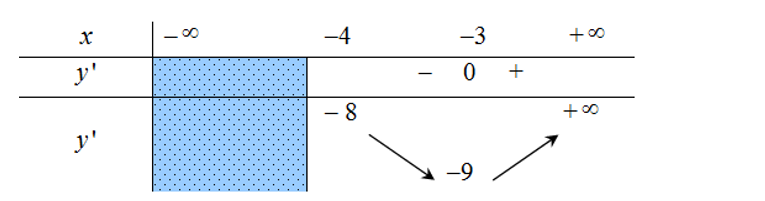
Dựa vào bảng biến thiên ta thấy, hàm số không có giá trị lớn nhất.

Giá trị nhỏ nhất của hàm số là – 9 tại x = – 3.

II. Cách tính giá trị  lớn nhất và giá trị nhỏ nhất của hàm số trên một đoạn

1. Định lí.

Mọi hàm số liên tục trên một đoạn đều có giá trị lớn nhất và giá trị nhỏ nhất trên đoạn đó.

2. Quy tắc tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một đoạn.

- Nhận xét:

Nếu đạo hàm f’(x) giữ nguyên dấu trên đoạn [a; b] thì hàm số đồng biến hoặc nghịch biến trên cả đoạn. Do đó, f(x) đạt được giá trị lớn nhất và giá trị nhỏ nhất tại các đầu mút của đoạn.

Nếu chỉ có một số hữu hạn các điểm x_i (x_i < x_{i+ 1}) mà tại đó f’(x) bằng 0 hoặc không xác định thì hàm số y = f(x) đơn điệu trên mỗi khoảng (x_i;  x_i+1). Rõ ràng, giá trị lớn nhất (giá trị nhỏ nhất) của hàm số trên đoạn [a; b] là số lớn nhất (số nhỏ nhất) trong các giá trị của hàm số tại hai đầu mút a; b và tại các điểm x_i nói trên.

- Quy tắc:

1. Tìm các điểm x₁; x₂; …; x_n trên khoảng (a; b), tại đó f’(x) bằng 0 hoặc f’(x) không xác định.

2. Tính f(a); f(x₁); f(x₂); ….; f(x_n); f(b).

3. Tìm số lớn nhất M và số nhỏ nhất m trong các số trên. Ta có:

$M=\underset{\text{[}a;b\text{]}}{\max }f\left(x\right);$$\hspace{0.17em}m=\underset{\text{[}a;b\text{]}}{\min }f\left(x\right)$

- Chú ý: Hàm số liên tục trên một khoảng có thể không có giá trị lớn nhất và giá trị nhỏ nhất trên khoảng đó. Chẳng hạn hàm số $f\left(x\right)=\frac{1}{x}$ không có giá trị lớn nhất, giá trị nhỏ nhất trên khoảng (0; 1).

Tuy nhiên, cũng có những hàm số có giá trị lớn nhất hoặc giá trị nhỏ nhất trên một khoảng như ví dụ sau:

Ví dụ 2. Tìm giá trị lón nhất, nhỏ nhất của hàm số $y=\sqrt{2x-x^2}$ trên khoảng $\left(0;\frac{3}{2}\right)$.

Lời giải:

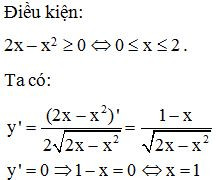
Bảng biến thiên:

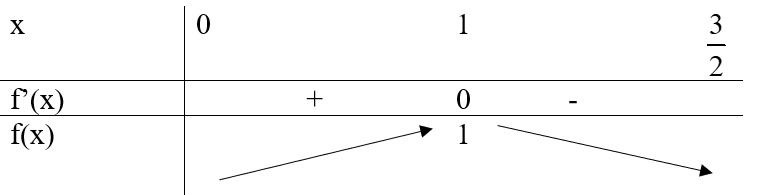
Từ bảng biến thiên trên ta thấy, trên khoảng $\left(0;\frac{3}{2}\right)$ hàm số có 1 điểm cực trị duy nhất là điểm cực đại x = 1 và tại đó hàm số đạt giá trị lớn nhất $\underset{\left(0;\frac{3}{2}\right)}{Max}f\left(x\right)=f\left(1\right)=1$.

B. Bài tập

I. Bài tập trắc nghiệm

Bài 1 Giá trị nhỏ nhất của hàm số $f\left(x\right)=x^4-10x^2-2$ trên đoạn $\left[0;9\right]$ bằng:

A. -2

B. -11

C. -26

D. -27

Lời giải

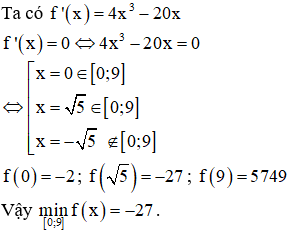
Chọn D.

Bài 2 Trên đoạn $[-2;1]$, hàm số $y=x^3-3x^2-1$ đạt giá trị lớn nhất tại điểm:

A. $x=-2$

B. $x=0$

C. $x=-1$

D. $x=1$ .

Lời giải

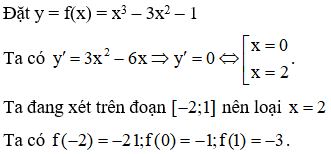
Do đó giá trị lớn nhất của hàm số trên đoạn $[-2;1]$ là -1, tại  x =0.

Chọn B.

Bài 3 Tìm giá trị lớn nhất  của hàm số $f\left(x\right)=\sqrt{x-1}+\sqrt{3-x}-2\sqrt{-x^2+4x-3}$

A. $M=0.$

B. $M=-\sqrt{2}.$

C. $M=\sqrt{2}.$

D. $M=\frac{9}{4}.$

Lời giải

TXĐ: Đặt  $\text{D}=\left[1;3\right].$

Chọn C.

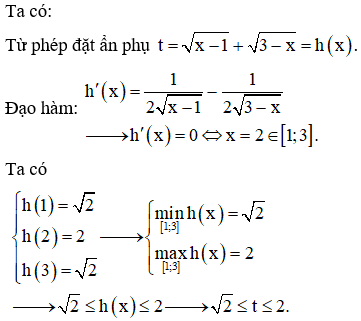
Bài 4 Tìm giá trị lớn nhất M của hàm số $f\left(x\right)=\left|-x^2-4x+5\right|$ trên đoạn $\left[-6;6\right]$.

A. $M=0.$

B. $M=9$

C. $M=55$

D. $M=110.$

Lời giải

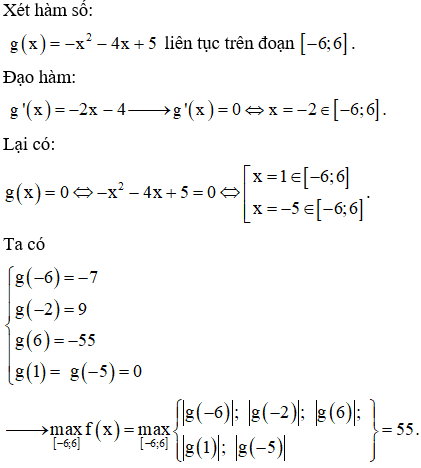
Chọn C.

Lưu ý: Hàm trị tuyệt đối không âm.

Bài 5 Tìm giá trị nhỏ nhất m của hàm số $f\left(x\right)=2{\cos }^{3}x-\frac{9}{2}{\cos }^{2}x+3\cos x+\frac{1}{2}$

A. $m=-24.$

B. $m=-12$

C. $m=-9.$

D. $m=-1$

Lời giải

Đặt $t=\cos x\left(-1\le t\le 1\right).$

Khi đó, bài toán trở thành Tìm giá trị nhỏ nhất của hàm số $g\left(t\right)=2t^3-\frac{9}{2}{t}^2+3t+\frac{1}{2}$ trên đoạn $\left[-1;1\right]\text{'}\text{'}$.

Đạo hàm:

$$\begin{gathered} g\text{'}\left(t\right)=6t^2-9t+3\stackrel{}{\to }g\text{'}\left(t\right)=0 \\ \iff \left[\begin{array}{l}t=1\in \left[-1;1\right]\\ t=\frac{1}{2}\in \left[-1;1\right]\end{array}\right.. \end{gathered}$$

Ta có :

$$\begin{gathered} \left\{\begin{array}{l}g\left(-1\right)=-9\\ g\left(\frac{1}{2}\right)=\frac{9}{8}\\ g\left(1\right)=1\end{array}\right.\stackrel{}{\to }\underset{\left[-1;1\right]}{\min }g\left(t\right) \\ =g\left(-1\right)=-9\stackrel{}{\to }\underset{x\in ℝ}{\min }f\left(x\right)=-9. \end{gathered}$$

Chọn C.

Bài 6 Giá trị lớn nhất của hàm số $f\left(x\right)=\frac{x-m^2}{x+1}$ trên đoạn $\left[0;1\right]$ bằng:

A. $\frac{1+m^2}{2}$

B. $-m^2$

C. $\frac{1-m^2}{2}$

D. $m^2$

Lời giải:

Đạo hàm :

$f\text{'}\left(x\right)=\frac{1+m^2}{{\left(x+1\right)}^2}>0,\forall x\in \left[0;1\right]$

Suy ra hàm số $f\left(x\right)$ đồng biến trên [ 0;1]

$\left[0;1\right]\stackrel{}{\to }\underset{\left[0;1\right]}{\max }f\left(x\right)=f\left(1\right)=\frac{1-m^2}{2}.$

Chọn C.

Bài 7 Tìm giá trị lớn nhất của hàm số $f\left(x\right)=x^3-2x^2-4x+1$  trên đoạn $\left[1;3\right].$

A. $\underset{\left[1;3\right]}{\max }f\left(x\right)=\frac{67}{27}.$

B. $\underset{\left[1;3\right]}{\max }f\left(x\right)=-2.$

C. $\underset{\left[1;3\right]}{\max }f\left(x\right)=-7.$

D. $\underset{\left[1;3\right]}{\max }f\left(x\right)=-4.$

Đáp án: B

Lời giải:

 $f\text{'}\left(x\right)=3x^2-4X-4$$\to f\text{'}\left(x\right)=0$

$\iff \left[\begin{array}{l}x=2\in \left[1;3\right]\\ x=-\frac{2}{3}\notin \left[1;3\right]\end{array}\right.$

Ta có $\left\{\begin{array}{l}\begin{array}{c}f\left(1\right)=-4\\ f\left(2\right)=-7\\ f\left(3\right)=-2\end{array}\\ \end{array}\right.$

$\to \underset{\left[1:3\right]}{max} f\left(x\right)=-2$

Cách 2. Sử dụng chức năng MODE 7 và nhập hàm $f\left(X\right)=X^3-2X^2-4X+1$ với thiết lập Start 1, End 3 Step 0.2.

Quan sát bảng giá trị F ( X ) ta thấy giá trị lớn nhất F ( X ) bằng - 2  khi X = 3

Bài 8  Gọi $M,m$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $f\left(x\right)=2x^3+3x^2-1$ trên đoạn $\left[-2;-\frac{1}{2}\right]$. Tính P = M - m.

A. $P=-5$.

B. $P=1$.

C. $P=4$.

D. $P=5$.

Bài 9 Biết rằng hàm số $f\left(x\right)=x^3-3x^2-9x+28$ đạt giá trị nhỏ nhất trên đoạn $\left[0;4\right]$ tại $x_0$ . Tính  $P=x_0+2018.$

A. $P=3.$

B. $P=2019.$

C. $P=2021.$

D. $P=2018.$

Đáp án: C

Lời giải:

Đạo hàm $f\text{'}\left(x\right)=3x^2-6x-9$

$\to f\text{'}\left(x\right)=0$

$\iff \left[\begin{array}{l}x=-1\notin \left[0;4\right]\\ x=3\in \left[0;4\right]\end{array}\right.$

Ta có  $\left\{\begin{array}{c}f\left(0\right)=28\\ f\left(3\right)=1\\ f\left(4\right)=8\end{array}\right.$

$\to \underset{\left[0;4\right]}{min} f\left(x\right)=1$khi x = 3 = $x_0$

$\to P=2021$

Bài 10. Xét hàm số $f\left(x\right)=-\frac{4}{3}{x}^3-2x^2-x-3$  trên $\left[-1;1\right]$. Mệnh đề nào sau đây là đúng?

A. Hàm số có giá trị nhỏ nhất tại $x=-1$  và giá trị lớn nhất tại $x=1$.

B. Hàm số có giá trị nhỏ nhất tại $x=1$ và giá trị lớn nhất tại $x=-1$.

C. Hàm số có giá trị nhỏ nhất tại $x=-1$ nhưng không có giá trị lớn nhất.

D. Hàm số không có giá trị nhỏ nhất nhưng có giá trị lớn nhất tại $x=1$.

Đáp án: B

Lời giải:

Đạo hàm $f\text{'}\left(x\right)=-4x^2-4x-1$

$=-{(2x-1)}^2\le 0\forall x\in R$

Suy ra hàm số f ( x ) nghịch biến trên đoạn $\left[-1 , 1\right]$ nên có giá trị nhỏ nhất tại  x = 1  và giá trị lớn nhất tại  x = - 1.

Bài 11 (ĐỀ MINH HỌA 2016 – 2017) Tìm giá trị nhỏ nhất của hàm số $f\left(x\right)=\frac{x^2+3}{x-1}$ trên đoạn.

A.$\underset{\left[2;4\right]}{\min }f\left(x\right)=6$.

B.$\underset{\left[2;4\right]}{\min }f\left(x\right)=-2\left[2;4\right]$.

C.$\underset{\left[2;4\right]}{\min }f\left(x\right)=-3$.

D.$\underset{\left[2;4\right]}{\min }f\left(x\right)=\frac{19}{3}$.

Đáp án: A

Giải thích:

Đạo hàm 

 $f\text{'}\left(x\right)=\frac{x^2-2x-3}{{\left(x-1\right)}^2}$

$\stackrel{}{\to }f\text{'}\left(x\right)=0$

$\iff [\begin{array}{l}x=-1\notin [2;4]\\ x=3\in [2;4]\end{array}$

Ta có  $\left\{\begin{array}{l}f\left(2\right)=7\\ f\left(3\right)=6\\ f\left(4\right)=\frac{19}{3}\end{array}\right.$

$\stackrel{}{\to }\underset{[2;4]}{\min }f\left(x\right)=6.$

Cách 2: Sử dụng công cụ TABLE (MODE 7).

Bước 1: Bấm tổ hợp phím MODE 7.

Bước 2: Nhập  $f\left(X\right)=\frac{X^2+3}{X-1}.$

Sau đó ấn phím = (nếu có g(X) thì ấn tiếp phím =) sau đó nhập  $\left\{\begin{array}{l}\text{Start}=2\\ \text{End}=4\\ \text{Step}=0.2\end{array}\right..$

(Chú ý: Thường ta chọn  $\text{Step}=\frac{\text{End}-\text{Start}}{10}$)

Dựa vào bảng giá trị ở trên, ta thấy $\underset{\left[2;4\right]}{\min }f\left(x\right)=f\left(3\right)=6.$

II. Bài tập tự luận có lời giải

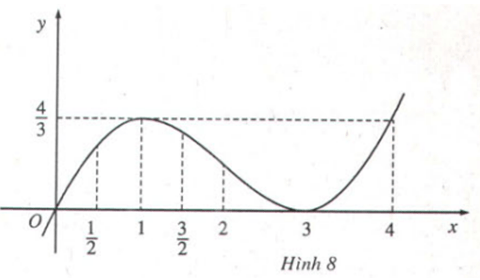
Bài 1 Dựa vào đồ thị (H.7, H.8), hãy chỉ ra các điểm tại đó mỗi hàm số sau có giá trị lớn nhất (nhỏ nhất):

a) y = -x² + 1 trong khoảng (-∞; +∞);

b) y = $\frac{x}{3}$(x+ 3)² trong các khoảng ($\frac{1}{2}; \frac{3}{2}$) và ($\frac{3}{2}$; 4).

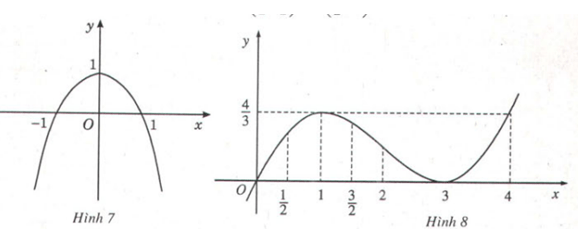
Lời giải:

a) Tại x = 0 hàm số có giá trị lớn nhất bằng 1.

Xét dấu đạo hàm:

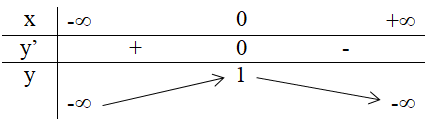
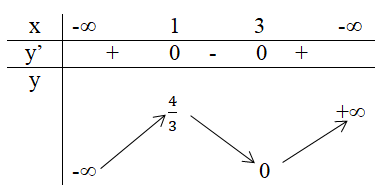
b) Tại x = 1 hàm số có giá trị lớn nhất bằng $\frac{4}{3}$.

Tại x = 3 hàm số có giá trị nhỏ nhất bằng 0.

Xét dấu đạo hàm:

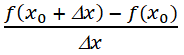Bài 2 Giả sử f(x) đạt cực đại tại x_o. Hãy chứng minh khẳng định 3 trong chú ý trên bằng cách xét giới hạn tỉ số  khi Δ$\overrightarrow{x}$ 0 trong hai trường hợp Δx > 0 và Δx < 0.

Bài 3

a) Sử dụng đồ thị, hãy xem xét các hàm số sau đây có cực trị hay không.

• y = -2x + 1;

• y = $\frac{x}{3}$(x-3)² (H.8).

b) Nêu mối quan hệ giữa sự tồn tại cực trị và dấu của đạo hàm.

Lời giải:

a,Hàm số y = -2x + 1 không có cực trị.

Hàm số y = $\frac{x}{3}$ (x-3)² đạt cực đại tại x = 1 và đạt cực tiểu tại x = 3.

b, Nếu hàm số có cực trị thì dấu của đạo hàm bên trái và bên phải điểm cực trị sẽ khác nhau.

Bài 4 Chứng minh hàm số y = |x| không có đạo hàm tại x = 0. Hàm số có đạt cực trị tại điểm đó không ?

Lời giải:

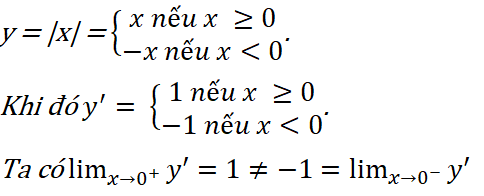
Vậy không tồn tại đạo hàm của hàm số tại x = 0.

Nhưng dựa vào đồ thị của hàm số y = |x|. Ta có hàm số đạt cực trị tại x = 0.

Bài 5 Áp dụng quy tắc I, hãy tìm các điểm cực trị của hàm s f(x) = x(x² – 3).

Lời giải:

1. TXĐ: D = R

2. f’(x) = 3x² – 3. Cho f’(x) = 0 ⇔ x = 1 hoặc x = -1.

3. Ta có bảng biến thiên:

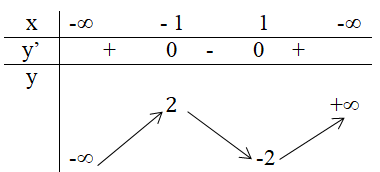
Hàm số đạt cực đại tại x = -1 và giá trị cực đại là 2

Hàm số đạt cực tiểu tại x = 1 và giá trị cực tiểu là -2.

Bài 6 Áp dụng Quy tắc 1, hãy tìm các điểm cực trị của các hàm số sau:

a) y = 2x³ + 3x² - 36x - 10

b) y = x⁴ + 2x² - 3;

c) y = x + $\frac{1}{x}$

d) y = x³(1 - x)²;

Lời giải:

a) TXĐ: D = R

y' = 6x² + 6x - 36

y' = 0 ⇔ x = -3 hoặc x = 2

Bảng biến thiên:

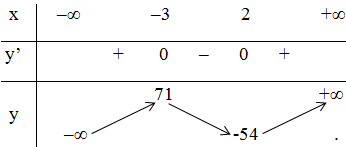
Kết luận :

Hàm số đạt cực đại tại x = -3 ; y_CĐ = 71

Hàm số đạt cực tiểu tại x = 2; y_CT = -54.

b) TXĐ: D = R

y'= 4x³ + 4x = 4x(x² + 1) = 0;

y' = 0 ⇔ x = 0

Bảng biến thiên:

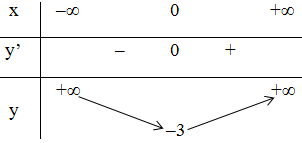
Vậy hàm số đạt cực tiểu tại x = 0; y_CT = -3

       hàm số không có điểm cực đại.

c) TXĐ: D = R \ {0}

y' = 1.  $\frac{1}{x^2}$

y' = 0 ⇔ x = ±1

Bảng biến thiên:

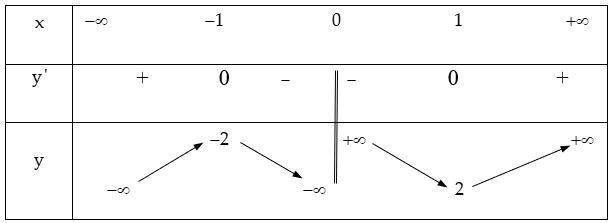
Vậy hàm số đạt cực đại tại x = -1; y_CĐ = -2;

       hàm số đạt cực tiểu tại x = 1; y_CT = 2.

d) TXĐ: D = R

y'= (x³)’.(1 – x)² + x³.[(1 – x)²]’

= 3x².(1 – x)² + x³.2(1 – x).(1 – x)’

= 3x²(1 – x)² - 2x³(1 – x)

= x².(1 – x)(3 – 5x)

y' = 0 ⇔ x = 0; x = 1 hoặc x = $\frac{3}{5}$

Bảng biến thiên:

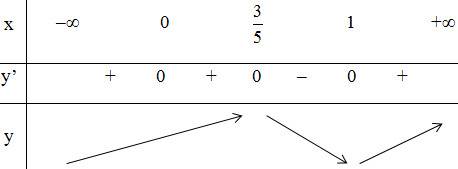
Vậy hàm số đạt cực đại tại x = $\frac{3}{5}$

       hàm số đạt cực tiểu tại x_CT = 1.

(Lưu ý: x = 0 không phải là cực trị vì tại điểm đó đạo hàm bằng 0 nhưng đạo hàm không đổi dấu khi đi qua x = 0.)

e) Tập xác định: D = R.

y' = 0 ⇔ x = $\frac{1}{2}$

Bảng biến thiên:

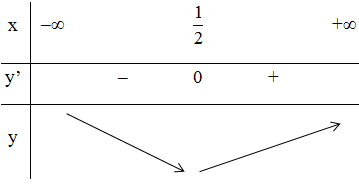
Vậy hàm số đạt cực tiểu tại x = $\frac{1}{2}$

Bài 7 Áp dụng Quy tắc 2, hãy tìm các điểm cực trị của hàm số sau:

a) y = x⁴ - 2x² + 1 ;

b) y = sin2x – x

c) y = sinx + cosx ;

d) y = x⁵ - x³ - 2x + 1

Lời giải:

a) TXĐ: D = R.

+ y' = 4x³ - 4x

y' = 0 ⇔ 4x(x² – 1) = 0 ⇔ x = 0 hoặc x = ±1.

+ y" = 12x² - 4

y"(0) = -4 < 0 ⇒ x = 0 là điểm cực đại của hàm số.

y"(1) = 8 > 0 ⇒ x = 1 là điểm cực tiểu của hàm số.

y"(-1) = 8 > 0 ⇒ x = -1 là điểm cực tiểu của hàm số.

b) TXĐ: D = R

+ y' = 2cos2x – 1;

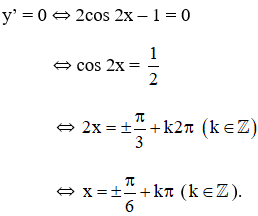
+ y" = -4.sin2x

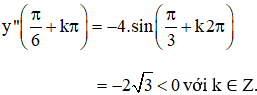
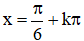⇒  (k ∈ Z) là các điểm cực đại của hàm số.

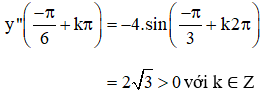
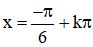⇒  (k ∈ Z) là các điểm cực tiểu của hàm số.

c) TXĐ: D = R

+ y’ = cos x – sin x.

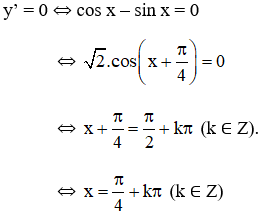
+ y’’ = -sin x – cos x =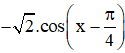 

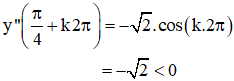
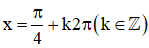⇒  là các điểm cực đại của hàm số.

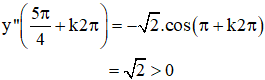
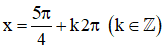⇒  là các điểm cực tiểu của hàm số.

d) TXĐ: D = R

+ y'= 5x⁴ - 3x² - 2

y' = 0 ⇔ 5x⁴ – 3x² – 2 = 0

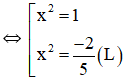
⇔ x = ±1.

+ y" = 20x³ - 6x

y"(-1) = -20 + 6 = -14 < 0

⇒ x = -1 là điểm cực đại của hàm số.

y"(1) = 20 – 6 = 14 > 0

⇒ x = 1 là điểm cực tiểu của hàm số.

Bài 8 Hàm số nào sau đây không có giá trị nhỏ nhất và giá trị lớn nhất trên đoạn [-2;2]?

Lời giải:

TXĐ: $\text{D}=\left[-\sqrt{2};\sqrt{2}\right].$ Đạo hàm $f^{\text{'}}\left(x\right)=1-\frac{x}{\sqrt{2-x^2}}$

$\stackrel{}{\to }{f}^{\text{'}}\left(x\right)=0$

$\iff \frac{x}{\sqrt{2-x^2}}=1$

$\iff \sqrt{2-x^2}=x$

 $\iff \{\begin{array}{l}x\ge 0\\ 2-x^2=x^2\end{array}$

$\iff x=1\in [-\sqrt{2};\sqrt{2}].$

Ta có  $\left\{\begin{array}{l}f\left(-\sqrt{2}\right)=-\sqrt{2}\\ f\left(1\right)=2\\ f\left(\sqrt{2}\right)=\sqrt{2}\end{array}\right.$

$\stackrel{}{\to }m=-\sqrt{2}.$

Bài 9 Tìm tất cả các giá trị của tham số m để hàm số y = x³ - 2x² +mx + 1 đạt cực đại tại x = 1.

Lời giải:

Ta có y' = 3x² - 4x + m

Hàm số đạt cực trị tại x = 1 thì y'(1) = 0 ⇒ 3.1² - 4.1 + m = 0 ⇒ m = 1

Với m = 1 thì hàm số đã cho trở thành y = x³ - 2x² + x + 1

Ta có y' = 3x² - 4x + 1, y'' = 6x - 4 Vì y''(1) = 2 > 0 nên hàm số đạt cực tiểu tại x = 1.

Do vậy không có m thỏa mãn.

Bài 10 Tìm điểm cực đại của hàm số y = sin²x + $\sqrt{3}$cosx + 1 với x ∈ (0; π)

Lời giải:

III. Bài tập vận dụng

Bài 1 Cho hàm số y = x⁴ - 2(m - 1)x² + m². Tìm m để hàm số có 3 điểm cực trị là 3 đỉnh của 1 tam giác vuông

Bài 2 Cho hàm số f có đạo hàm là f'(x) = x(x+1)²(x-2)⁴ với mọi x ∈ R. Số điểm cực trị của hàm số f là?

Bài 3 Điểm cực đại của hàm số y = -x³ - 3x² + 1 là?

Bài 4 Điểm cực tiểu của hàm số y = x⁴ + 4x² + 2 là?

Bài 5 Tìm a, b, c sao cho hàm số y = x³ + ax² + bx + c có giá trị bằng 0 khi x = 1 và đạt cực trị khi bằng 0 khi x = -1 .

Bài 6 Giá trị của m để hàm số y = x³ - 3mx² + (m² - 1)x + 2 đạt cực đại tại x = 2 là?

Bài 7 Với giá trị nào của m, hàm số y = (x - m)³ - 3x đạt cực tiểu tại điểm có hoành độ x = 0?

Bài 8 Với giá trị nào của m, hàm số y = x³ + 2(m - 1)x² + (m² - 4m + 1)x + 2(m² + 1) có hai điểm cực trị x₁,x₂ thỏa mãn

Bài 9 Với giá trị nào của m, đồ thị hàm số y = x³ - mx² + 3(m² - 1)x - m ³ + m có điểm cực đại B, điểm cực tiểu C thỏa mãn OC = 3OB, với O là gốc tọa độ?

Bài 10 Với giá trị nào của m, đồ thị hàm số y = x³ - 3mx² + m có hai điểm cực trị B, C thẳng hàng với điểm A(-1;3)?