Toptailieu.vn biên soạn và giới thiệu Chuyên đề Ôn tập chương 3 gồm đầy đủ các phần: Lý thuyết, phương pháp giải, bài tập minh họa có lời giải chi tiết giúp học sinh làm tốt bài tập Toán 12 từ đó học tốt môn Toán. Mời các bạn đón xem:

Ôn tập chương 3: Lý thuyết, cách giải và bài tập hay, chi tiết

A. Lý thuyết

1. Nguyên hàm và tính chất

1.1 Nguyên hàm.

- Định nghĩa

Cho hàm số f(x) xác định trên K (K là khoảng, đoạn hay nửa khoảng của R). 

Hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên K nếu F’(x) = f(x) với mọi $x\in K$.

Ví dụ.

- Hàm số F(x) = sinx + 6 là một nguyên hàm của hàm số f(x) = cosx trên khoảng $\left(-\infty ;+\infty \right)$ vì F’(x) = (sinx + 6)’ = cosx với $\forall x\in \left(-\infty ;+\infty \right)$.

- Hàm số $F\left(x\right)=\frac{x+\text{\hspace{0.17em}}2}{x-3}$ là một nguyên hàm của hàm số $f\left(x\right)=\frac{-5}{{(x-3)}^2}$ trên khoảng $(-\infty ;3)\cup (3;+\text{\hspace{0.17em}}\infty )$

Vì $F\text{'}\left(x\right)={\left(\frac{x+\text{\hspace{0.17em}}2}{x-3}\right)}^{\text{'}}$$=\frac{-5}{{(x-3)}^2}=f\left(x\right)$ với $\forall x\in (-\infty ;3)\cup (3;+\infty )$

- Định lí 1.

 Nếu F(x) là một nguyên hàm của f(x) trên K thì với mỗi hằng số C, hàm số G(x) = F(x) + C cũng là một nguyên hàm của f(x) trên K.

- Định lí 2.

Nếu F(x) là một nguyên hàm của hàm số f(x) trên K thì mọi nguyên hàm của f(x) trên K đều có dạng F(x) + C, với C là một hằng số.

Do đó $F\left(x\right)+C;C\in ℝ$ là họ tất cả các nguyên hàm của f(x) trên K.

Kí hiệu: $\underset{}{\overset{}{\int }}f\left(x\right)\text{}dx=F\left(x\right)+C$

- Chú ý: Biểu thức f(x)dx chính là vi phân của nguyên hàm F(x) của f(x), vì dF(x) = F’(x)dx = f(x)dx.

Ví dụ.

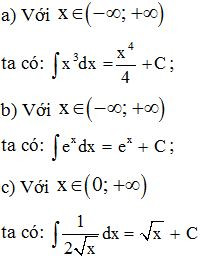
1.2 Tính chất của nguyên hàm

Ví dụ. Tìm nguyên hàm của hàm số $f\left(x\right)=3x^2+\text{\hspace{0.17em}\hspace{0.17em}}2\sin x$ trên khoảng $\left(-\infty ;+\infty \right)$.

Lời giải:

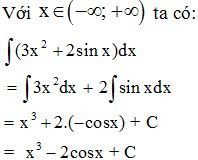
1.3 Sự tồn tại nguyên hàm

Định lí:

Mọi hàm số f(x) liên tục trên K đều có nguyên hàm trên K.

Ví dụ.

a) Hàm số $y=\sqrt{x}$ có nguyên hàm trên khoảng $\left(0;+\infty \right)$.

$\int \sqrt{x}dx=\int x^{\frac{1}{2}}dx$$=\frac{2}{3}{x}^{\frac{3}{2}}+C=\frac{2}{3}x\sqrt{x}+C$

b) Hàm số y = $\frac{1}{x}$ có nguyên hàm trên khoảng $\left(-\infty ;0\right)\cup \left(0;+\infty \right)$

$\int \frac{1}{x}dx=\ln \left|x\right|+\text{\hspace{0.17em}\hspace{0.17em}}C$

1.4 Bảng nguyên hàm của một số hàm số thường gặp

Ví dụ. Tính:

a) $\int \left(3x^4+\text{\hspace{0.17em}\hspace{0.17em}}\sqrt[3]{x}\right)dx$

b) $\int (5e^x-4^{x+\text{\hspace{0.17em}}2})dx$

Lời giải:

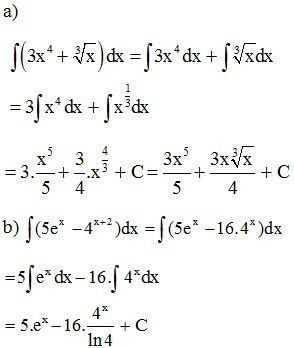
- Chú ý: Từ đây, yêu cầu tìm nguyên hàm của một hàm số được hiểu là tìm nguyên hàm trên từng khoảng xác định của nó.

2. Phương pháp tính nguyên hàm.

2.1 Phương pháp đổi biến số

- Định lí 1.

Nếu $\int f\left(u\right)du=F\left(u\right)+\text{\hspace{0.17em}\hspace{0.17em}}C$ và u = u(x) là hàm số có đạo hàm liên tục thì:

$\int f\left(u\right(x\left)\right).u\text{'}\left(x\right)dx$$=F\left(u\right(x\left)\right)+C$

Hệ quả: Nếu u = ax + b (a ≠ 0), ta có:

$\int f(ax+\text{\hspace{0.17em}}b)dx$$\hspace{0.17em}=\frac{1}{a}F(ax+\text{\hspace{0.17em}}b)+\text{\hspace{0.17em}}C$

Ví dụ. Tính $\int {(3x+\text{\hspace{0.17em}}2)}^{3}dx$.

Lời giải:

Ta có: $\int u^{3}du=\frac{u^4}{4}+\text{\hspace{0.17em}}C$ nên theo hệ quả ta có:

$\int {(3x+\text{\hspace{0.17em}}2)}^{3}dx$$\hspace{0.17em}=\frac{{(3x+2)}^4}{4}+\text{\hspace{0.17em}\hspace{0.17em}}C$

Chú ý:

Nếu tính nguyên hàm theo biến mới u (u = u(x)) thì sau khi tính nguyên hàm, ta phải trở lại biến x ban đầu bằng cách thay u bởi u(x).

Ví dụ. Tính $\int \sin x.c{\text{os}}^{2}xdx$.

Lời giải:

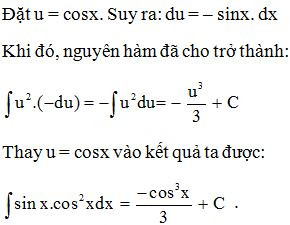
2.2 Phương pháp tính nguyên hàm từng phần.

- Định lí 2.

Nếu hai hàm số u = u(x) và v = v(x) có đạo hàm liên tục trên K thì:

$\int u\left(x\right).v\text{'}\left(x\right).dx$$=u\left(x\right).v\left(x\right)-\int u\text{'}\left(x\right).v\left(x\right)dx$

- Chú ý.

Vì u’(x) dx = du; v’(x) dx = dv. Nên đẳng thức trên còn được viết ở dạng:

$\int udv=uv-\int vdu$

Đó là công thức nguyên hàm từng phần.

Ví dụ. Tính

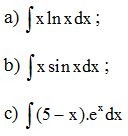
Lời giải:

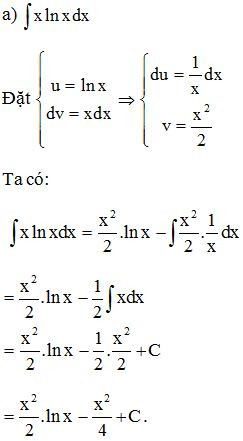
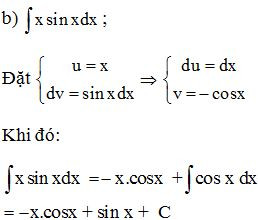
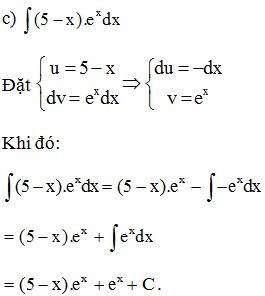
3. Khái niệm tích phân

3.1 Diện tích hình thang cong

- Cho hàm số y = f(x) liên tục, không đổi dấu trên đoạn [a; b]. Hình phẳng giới hạn bởi đồ thị của hàm số y = f(x), trục hoành và hai đường thẳng x = a; x = b được gọi là hình thang cong.

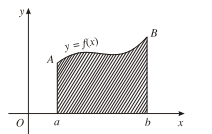
- Ta xét bài toán tìm diện tích hình thang cong bất kì:

Cho hình thang cong giới hạn bởi các đường thẳng x = a;  x = b (a < b); trục hoành và đường cong y = f(x), trong đó f(x) là hàm số liên tục, không âm trên đoạn [a; b].

Với mỗi $x\in \left[a;b\right]$, kí hiệu S(x) là diện tích của phần hình thang cong đó nằm giữa hai đường thẳng vuông góc với Ox lần lượt tại a và b.

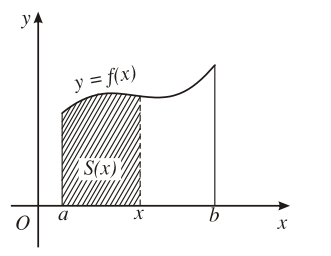
Ta chứng minh được S(x) là một nguyên hàm của f(x) trên đoạn [a; b].

Giả sử F(x) cũng là một nguyên hàm của f(x) thì có một hằng số C sao cho S(x) = F(x) +  C.

Vì S(a) = 0 nên F(a) +  C = 0  hay C =  –  F(a).

Vậy S(x) = F(x) – F(a).

Thay x = b vào đẳng thức trên, ta có diện tích của hình thang cần tìm là:

S(b) = F(b) – F(a).

3.2 Định nghĩa tích phân

Cho f(x) là hàm số liên tục trên đoạn [a; b]. Giả sử F(x) là một nguyên hàm của f(x) trên đoạn [a; b].

Hiệu số F(b) – F(a) được gọi là tích phân từ a đến b (hay tích phân xác định trên đoạn [a; b]) của hàm số f(x), kí hiệu $\underset{a}{\overset{b}{\int }}f\left(x\right)dx$.

Ta còn dùng kí hiệu  để chỉ hiệu số F(b) – F(a).

Vậy $\underset{a}{\overset{b}{\int }}f\left(x\right)dx$$=F{\left(x\right)}_a^b=F\left(b\right)-F\left(a\right)$

Ta gọi $\underset{a}{\overset{b}{\int }}$ là dấu tích phân, a là cận dưới, b là cận trên, f(x)dx là biểu thức dưới dấu tích phân và f(x) là hàm số dưới dấu tích phân.

- Chú ý.

Trong trường hợp a = b hoặc a > b, ta quy ước:

$\underset{a}{\overset{a}{\int }}f\left(x\right)dx=0;$$\underset{a}{\overset{b}{\int }}f\left(x\right)\text{}dx=-\underset{b}{\overset{a}{\int }}f\left(x\right)\text{}dx$

Ví dụ.

a) $\underset{0}{\overset{2}{\int }}(x+\text{}2)dx$

$$\begin{gathered} ={\left.\left(\frac{x^2}{2}+2x\right)\right|}_0^2 \\ =6-0=6 \end{gathered}$$

b) $\underset{0}{\overset{\frac{\pi }{2}}{\int }}(2+\text{\hspace{0.17em}}\cos x)dx$

$$\begin{gathered} ={\left.\left(2x+\text{\hspace{0.17em}\hspace{0.17em}}\sin x\right)\right|}_0^{\frac{\pi }{2}} \\ =(\pi +1)-0 \\ =\mathrm{\pi }+1 \end{gathered}$$

- Nhận xét.

a) Tích phân của hàm số f từ a đến b có thể kí hiệu là $\underset{a}{\overset{b}{\int }}f\left(x\right)dx$ hay $\underset{a}{\overset{b}{\int }}f\left(t\right)dt$. Tích phân đó chỉ phụ thuộc vào f và các cận a, b mà không phụ thuộc vào biến x hay t.

b) Ý nghĩa hình học của tích phân.

Nếu hàm số f(x) liên tục và không âm trên đoạn [a; b] thì tích phân $\underset{a}{\overset{b}{\int }}f\left(x\right)dx$ là diện tích S của hình thang cong giới hạn bởi đồ thị của f(x), trục Ox và hai đường thẳng x = a; x = b. Vậy $S\text{\hspace{0.17em}}=\underset{a}{\overset{b}{\int }}f\left(x\right)dx$.

4. Tính chất của tích phân.

Ví dụ. Tính: $\underset{0}{\overset{\pi }{\int }}(3x-4\sin x)dx$.

Lời giải:

Ta có:

$\begin{array}{l}\underset{0}{\overset{\pi }{\int }}(3x-4\sin x)dx\\ =3\underset{0}{\overset{\pi }{\int }}xdx-4\underset{0}{\overset{\pi }{\int }}\sin xdx\\ =3{\left..\frac{x^2}{2}\right|}_0^{\pi }+\text{}{\left.4c\text{os x}\right|}_0^{\pi }\\ =\frac{3{\pi }^2}{2}+\text{\hspace{0.17em}}(-4-4)=\frac{3{\pi }^2}{2}-8\end{array}$

- Tính chất 3.

$\underset{a}{\overset{b}{\int }}f\left(x\right)dx$$=\underset{a}{\overset{c}{\int }}f\left(x\right)dx+\underset{c}{\overset{b}{\int }}f\left(x\right)dx$ (a < c < b).

Ví dụ. Tính $\underset{-2}{\overset{2}{\int }}\left|x\right|dx$.

Lời giải:

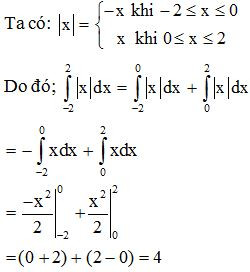
5. Phương pháp tính tích phân

5.1 Phương pháp đổi biến số

- Định lí:

Cho hàm số f(x) liên tục trên đoạn [a; b]. Giả sử hàm số $x=\phi \left(t\right)$ có đạo hàm liên tục trên đoạn $\left[\alpha ;\beta \right]$ sao cho $\phi \left(\alpha \right)=a;\phi \left(\beta \right)=b$ và $a\le \phi \left(t\right)\le b\forall t\in \left[\alpha ;\beta \right]$.

Khi đó: $\underset{a}{\overset{b}{\int }}f\left(x\right)\text{}dx$$\hspace{0.17em}=\underset{\alpha }{\overset{\beta }{\int }}f\left(\phi \left(t\right)\right).\phi \text{'}\left(t\right)dt$

Ví dụ.  Tính $\underset{0}{\overset{1}{\int }}\sqrt{1-x^2}dx$.

Lời giải:

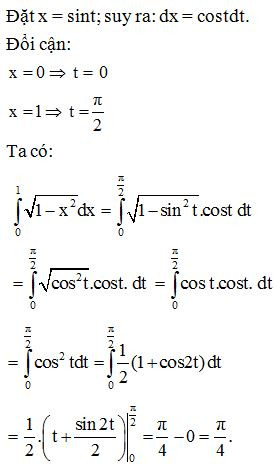
- Chú ý:

Trong nhiều trường hợp ta còn sử dụng phép đổi biến số ở dạng sau:

Cho hàm số f(x) liên tục trên đoạn [a; b]. Để tính $\underset{a}{\overset{b}{\int }}f\left(x\right)dx$, đôi khi ta chọn hàm số u = u(x) làm biến số mới, trong đó trên đoạn [a; b], u(x) có đạo hàm liên tục và $u\left(x\right)\in \left[\alpha ;\beta \right]$.

Giả sử có thể viết: f(x) = g(u(x)). u’(x) với $x\in \left[a;b\right]$ với g(u) liên tục trên đoạn $\left[\alpha ;\beta \right]$

Khi đó, ta có: $\underset{a}{\overset{b}{\int }}f\left(x\right)dx$$=\underset{u\left(a\right)}{\overset{u\left(b\right)}{\int }}g\left(u\right)du$

Ví dụ. Tính $\underset{0}{\overset{\sqrt{\pi }}{\int }}x.\sin x^{2}dx$.

Lời giải:

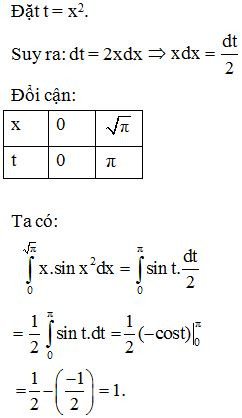
5.2 Phương pháp tính tích phân từng phần

- Định lí.

Nếu u = u(x) và v = v(x) là hai hàm số có đạo hàm liên tục trên đoạn [a; b] thì:

$\underset{a}{\overset{b}{\int }}u\left(x\right).v\text{'}\left(x\right)dx$$\hspace{0.17em}={\left[u\left(x\right).v\left(x\right)\right]}_a^b$$-\underset{a}{\overset{b}{\int }}v\left(x\right).u\text{'}\left(x\right)dx$

Hay $\underset{a}{\overset{b}{\int }}udv={\left.uv\right|}_a^b-\underset{a}{\overset{b}{\int }}vdu$

Ví dụ. Tính $I=\underset{0}{\overset{\frac{\pi }{2}}{\int }}x\sin xdx.$

Lời giải:

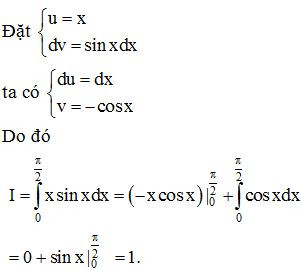
Ví dụ. Tính $I=\underset{0}{\overset{e-1}{\int }}x\ln (x+1)dx$.

Lời giải:

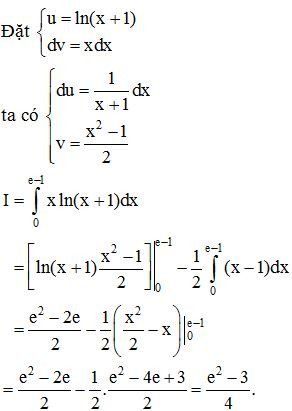
6. Tính diện tích hình phẳng

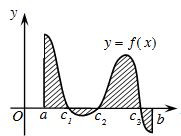
6.1 Hình phẳng giới hạn bởi một đường cong và trục hoành

Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x) liên tục trên đoạn [a; b], trục hoành và hai đường thẳng x = a; x = b được xác định: $S\text{\hspace{0.17em}\hspace{0.17em}}=\underset{a}{\overset{b}{\int }}\left|f\left(x\right)\right|dx$.

Ví dụ. Tính diện tích hình phẳng được giới hạn bởi y = 5x⁴ + 3x², trục hoành và hai đường thẳng x = 0; x = 1.

Lời giải:

Diện tích hình phẳng cần tính là:

$\begin{array}{l}S=\underset{0}{\overset{1}{\int }}\left|5x^4+3x^2\right|dx\\ =\underset{0}{\overset{1}{\int }}\left(5x^4+3x^2\right)dx\\ ={\left.\left(x^5+\text{\hspace{0.17em}}{x}^3\right)\right|}_0^1=2\end{array}$

6.2 Hình phẳng được giới hạn bởi 2 đường cong

Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x); y = g(x) liên tục trên đoạn [a; b] và hai đường thẳng x = a; x = b được xác định:

$S\text{\hspace{0.17em}\hspace{0.17em}}=\underset{a}{\overset{b}{\int }}\left|f\left(x\right)-g\left(x\right)\right|dx$(*).

- Chú ý.

Khi áp dụng công thức (*), cần khử dấu giá trị tuyệt đối của hàm số dưới dấu tích phân. Muốn vậy ta giải phương trình: f(x) – g(x) = 0 trên đoạn [a; b].

Giả sử phương trình có hai nghiệm c; d (c < d). Khi đó, f(x) – g(x) không đổi dấu trên các đoạn [a; c]; [c; d]; [d; b]. Trên mỗi đoạn đó, chẳng hạn trên [a; c] ta có:

$\underset{a}{\overset{c}{\int }}\left|f\left(x\right)-g\left(x\right)\right|dx$$\hspace{0.17em}=\left|\underset{a}{\overset{c}{\int }}\left[f\left(x\right)-g\left(x\right)\right]dx\right|$

Ví dụ. Tính diện tích hình phẳng được giới hạn bởi các đường thẳng x = 0; x = 2 và các đồ thị của hai hàm số y = x – 1 và y = x² – 1.

Lời giải:

Phương trình hoành độ giao điểm của hai đường cong:

7. Tính thể tích

7.1 Thể tích của vật thể

Cắt một vật thể (H) bởi hai mặt phẳng (P) và (Q) vuông góc với trục Ox lần lượt tại x = a; x = b (a < b) . Một mặt phẳng tùy ý vuông góc với Ox tại điểm x $(a\le x\le b)$ cắt (H) theo thiết diện có diện tích là S(x). Giả sử S(x) liên tục trên đoạn [a; b].

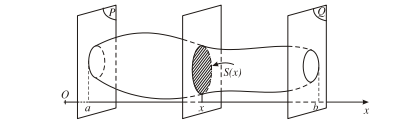
Khi đó, thể tích V của phần vật thể giới hạn bởi hai mặt phẳng (P) và (Q) được xác định bởi công thức: $V=\underset{a}{\overset{b}{\int }}S\left(x\right)dx$.

7.2 Thể tích khối chóp và khối chóp cụt.

a) Cho khối chóp có diện tích đáy là B, chiều cao h.

Khi đó, thể tích của khối chóp là $V=\frac{1}{3}B.h$.

b) Cho khối chóp cụt tạo bởi khối chóp đỉnh S có diện tích hai đáy lần lượt là B; B’ và chiều cao là h.

Thể tích của khối chóp cụt là:

$V=\frac{h}{3}\left(B+\sqrt{B.B\text{'}}+B\text{'}\right)$

8. Thể tích khối tròn xoay

 - Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường cong  y = f(x), trục hoành và hai đường thẳng x = a;  x = b quanh trục Ox:

$V=\pi \underset{a}{\overset{b}{\int }}{f}^2\left(x\right)dx$

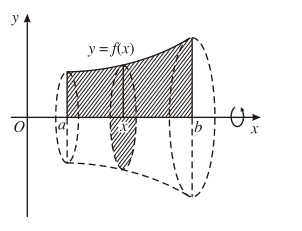
Ví dụ. Cho hình phẳng giới hạn bởi đường cong , trục hoành và hai đường thẳng x = 0; x = 2. Tính thể tích khối tròn xoay thu được khi quay hình này quanh trục Ox.

Lời giải:

Thể tích khối tròn xoay cần tính là:

$V=\pi \underset{0}{\overset{2}{\int }}{x}^{4}dx$$=\pi {\left.\frac{x^5}{5}\right|}_0^2=\frac{32\pi }{5}$

B. Bài tập

I. Bài tập trắc nghiệm

Câu 1: Họ nguyên hàm của hàm số

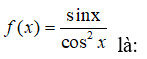
Lời giải:

Câu 2: Trong những phát biểu sau, phát biểu nào là sai?

Lời giải:

Câu 3: Tìm nguyên hàm của hàm số

Lời giải:

Câu 4:

A. I = x².sinx + x.cosx - 2sinx + C    

B. I = x².sinx + 2x.cosx - 2sinx + C

C. I = x.sinx + 2x.cosx + C    

D. I = 2x.cosx + sinx + C

Lời giải:

Câu 5:

A. I = ln3x - 2ln²x + 2lnx + C    

B. I = -ln3x - 2ln²x + 2lnx + C

C. I = ln3x + 2ln²x + 2lnx + C    

D. I = ln3x - 2ln²x - 2lnx + C

Lời giải:

Câu 6:

Lời giải:

Câu 7:

Lời giải:

Câu 8: Tích phân

với α ∈ [0; π] là:

A. αcosα - sinα    

B. αcosα + sinα

C. -αcosα + sinα    

D. -αcosα - sinα

Lời giải:

Câu 9: Cho tích phân

Phát biểu nào sau đây là sai:

Lời giải:

Câu 10: Diện tích hình phẳng giới hạn bởi đồ thị các hàm số y = x² và y = 2x là:

Lời giải:

Câu 1: Diện tích hình phẳng giới hạn bởi y = (e + 1)x và y = (1 + e^x)x là:

Lời giải:

Câu 2: Diện tích hình phẳng giới hạn bởi y = (x - 6)² và y = 6x - x² là:

Lời giải:

Câu 3: Diện tích hình phẳng giới hạn bởi đường cong: y = x² + 1 , tiếp tuyến với đường cong này tại M(2;5) và trục Oy là:

Lời giải:

Câu 4: Thể tích vật thể tròn xoay sinh ra bởi phép quay quanh trục Ox của hình phẳng giới hạn bởi trục Ox và y = $\sqrt{x}$sinx với (0 ≤ x ≤ π) là:

Lời giải:

Câu 5: Tính thể tích vật thể tròn xoay quanh trục Ox sinh bởi hình phẳng giới hạn bởi các đường

Lời giải:

Câu 6: Tính thể tích vật thể tròn xoay quanh trục Oy sinh bởi hình phẳng giới hạn bởi các đường y = 2, y = 4 , y = $\frac{x^2}{2}$ .

Lời giải:

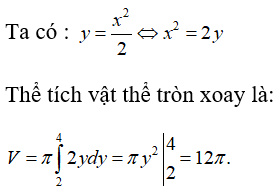
Câu 7: Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các đường y = tanx, y = 0, x = 0, x = $\frac{\mathrm{\pi }}{3}$ quanh Ox là:

Lời giải:

Câu 8: Diện tích hình phẳng giới hạn bởi ay = x² và ax = y² là:

Lời giải:

Câu 9: Một vật chuyển động với vận tốc

Quãng đường vật đi được sau 4s xấp xỉ bằng:

Lời giải:

Quãng đường vật di chuyển sau thời gian 4 giây bằng :

III. Bài tập vận dụng

Bài 1 Diện tích hình phẳng giới hạn bởi y = (e + 1)x và y = (1 + e^x)x là?

Bài 2 Diện tích hình phẳng giới hạn bởi y = (x - 6)² và y = 6x - x² là?

Bài 3 Diện tích hình phẳng giới hạn bởi đường cong: y = x² + 1 , tiếp tuyến với đường cong này tại M(2;5) và trục Oy là?

Bài 4 Thể tích vật thể tròn xoay sinh ra bởi phép quay quanh trục Ox của hình phẳng giới hạn bởi trục Ox và y = $\sqrt{x}$sinx với (0 ≤ x ≤ π) là?

Bài 5 Tính thể tích vật thể tròn xoay quanh trục Oy sinh bởi hình phẳng giới hạn bởi các đường y = 2, y = 4 , y = $\frac{x^2}{2}$ 

Bài 6 Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các đường y = tanx, y = 0, x = 0, x = $\frac{\mathrm{\pi }}{3}$ quanh Ox là?

Bài 7 Diện tích hình phẳng giới hạn bởi ay = x² và ax = y² là?

Bài 8 Một vật chuyển động với vận tốc

Bài 9 Quãng đường vật đi được sau 4s xấp xỉ bằng?

Bài 10 Diện tích hình phẳng giới hạn bởi đồ thị các hàm số y = x² và y = 2x là?