Toptailieu.vn biên soạn và giới thiệu Chuyên đề Phương trình bậc hai với hệ số thực gồm đầy đủ các phần: Lý thuyết, phương pháp giải, bài tập minh họa có lời giải chi tiết giúp học sinh làm tốt bài tập Toán 12 từ đó học tốt môn Toán. Mời các bạn đón xem:
Phép chia số phức: Lý thuyết, cách giải và bài tập hay, chi tiết
A. Lý thuyết
1. Tổng và tích của hai số phức liên hợp
Cho số phức z = a + bi, ta có:
= (a + bi) + (a – bi) = 2a;
= (a + bi). (a – bi) = a2 – (bi)2 = a2 + b2 =
Do đó:
+ Tổng của một số phức với số phức liên hợp của nó bằng hai lần phần thực của số phức đó.
+ Tích của một số phức với số phức liên hợp của nó bằng bình phương môđun của số phức đó.
Vậy tổng và tích của hai số phức liên hợp là một số thực.
2. Phép chia hai số phức
Chia số phức c + di cho số phức a + bi khác 0 là tìm số phức z sao cho
c + di = (a + bi).z. Số phức z được gọi là thương trong phép chia c + di cho a + bi và kí hiệu là: .
Ví dụ 1. Thực hiện phép chia 4 – 6i cho 1 + i.
Lời giải:
QUẢNG CÁO
Giả sử
Theo định nghĩa ta có: (1 + i).z = 4 – 6i.
Nhân cả hai vế với số phức liên hợp của 1 + i ta được:
(1 – i) .(1 + i).z = (1 – i).(4 – 6i)
Suy ra: 2z = – 2 – 10i
Do đó, z = –1 – 5i
Vậy .
– Tổng quát:
Giả sử . Theo định nghĩa phép chia số phức, ta có:
(a + bi).z = c + di
Nhân cả hai vế với số phức liên hợp của a + bi, ta được:
(a – bi)(a + bi).z = (a – bi)(c + di)
Hay (a2 + b2).z = (ac + bd) + (ad – bc).i
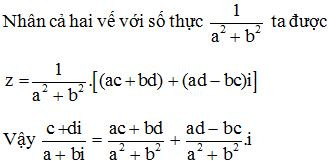
– Chú ý. Trong thực hành để tính thương , ta nhân cả tử và mẫu với số phức liên hợp của a + bi.
Ví dụ 2. Thực hiện phép chia 2 – 4i cho 2 + i.
Lời giải:
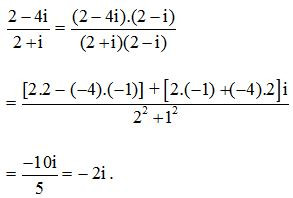
B. Bài tập
I. Bài tập trắc nghiệm
Bài 1: Các số thực x, y thỏa mãn
Khi đó, tổng T = x + y bằng
A. 4
B.5
C. 6
D. 7.
Lời giải:
Ta có
Vậy T = -2 + 8 = 6
Bài 2: Cho số phức z thỏa mãn (3 + 2i)z + (2 - i)2 = 4 + i. Môđun của số phức w = (z + 1)z− là
A. 2
B. 4
C. 10
D.
Lời giải:
Ta có:
Bài 3: Cho số phức z thỏa mãn 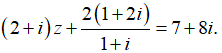
A. 3
B. 4
C. 5
D. 6.
Lời giải:
Bài 4: Nghịch đảo của số phức z = 1 - 2i là
Lời giải:
Ta có
Chọn đáp án D.
Bài 5: Số phức
A. -1+i
B.1-i
C. -1-i
D. 1+5i.
Ta có
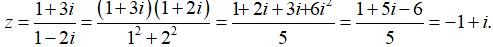
Chọn đáp án A.
Bài 6: Số phức z thỏa mãn z(1 + 2i) + 1 - i = 2i là
A. -1+i
B. 1-i
C. 1+i
D. -1-i.
Lời giải:
Ta có:z(1 + 2i) + 1 - i = 2i là <=> z(1 + 2i) = -1 + 3i
Do đó:
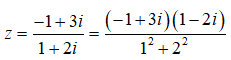
Chọn đáp án C.
Bài 7: Nghịch đảo của số phức z = 1 + i là
Lời giải:
Nghịch đảo của số phức z = 1 + i là
Bài 8: Phần thực và phần ảo của số phức
A. 0 và 1
B. 0 và i
C. 0 và -1
D. 0 và – i.
Lời giải:
Ta có
Vậy phần thực và phần ảo của z là 0 và -1
Bài 9: Cho số phức
Phần thực và phần ảo của số phức w = (z + 1)(z + 2) là
A. 2 và 1
B. 1 và 3
C. 2 và i
D. 1 và 3i.
Lời giải:
Ta có
Suy ra w = (z + 1)(z + 2) = (i + 1)(i + 2) = -1 + 2i + i + 2 = 1 + 3i
Vậy phần thực và phần ảo của w là 1 và 3
Bài 10: Số phức
Lời giải:
Ta có
II. Bài tập tự luận có lời giải
Bài 1: Cho số phức z thỏa mãn (2 + 3i)z = 1 Khi đó, + 2z bằng
Lời giải:
Ta có: (2 + 3i)z = 1 - 5i. Do đó
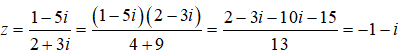
⇒ z− = -1 + i
Bài 2: Nghịch đảo của số phức z = 1 - 2i là?
Lời giải:
Ta có
Bài 3: Số phức
Lời giải:
Ta có
Câu 4: Số phức z thỏa mãn z(1 + 2i) + 1 - i = 2i là
Lời giải:
Ta có:z(1 + 2i) + 1 - i = 2i là <=> z(1 + 2i) = -1 + 3i
Do đó:
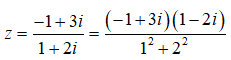
Câu 5: Nghịch đảo của số phức z = 1 + i là?
Lời giải:
Nghịch đảo của số phức z = 1 + i là
Câu 6: Phần thực và phần ảo của số phức
Lời giải:
Ta có
Vậy phần thực và phần ảo của z là 0 và -1
Câu 7: Cho số phức
Phần thực và phần ảo của số phức w = (z + 1)(z + 2) là
Lời giải:
Ta có
Suy ra w = (z + 1)(z + 2) = (i + 1)(i + 2) = -1 + 2i + i + 2 = 1 + 3i
Vậy phần thực và phần ảo của w là 1 và 3
Câu 8: Số phức
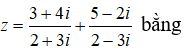
Lời giải:
Ta có
Câu 9: Cho số phức z thỏa mãn (2 + 3i)z = 1 Khi đó, z− + 2z bằng
Lời giải:
Ta có: (2 + 3i)z = 1 - 5i. Do đó
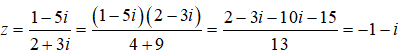
⇒ z− = -1 + i
Câu 10: Các số thực x, y thỏa mãn
Khi đó, tổng T = x + y bằng?
Lời giải:
Ta có
Vậy T = -2 + 8 = 6
III. Bài tập vận dụng
Bài 1 Cho số phức z thỏa mãn 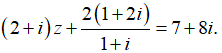
Bài 2 Cho số phức z thỏa mãn (3 + 2i)z + (2 - i)2 = 4 + i. Môđun của số phức w = (z + 1) là?
Bài 3 Cho số phức z thỏa mãn (2 + 3i)z = 1 Khi đó, + 2z bằng?
Bài 4 Cho z = 2 + 3i. Hãy tính z + và z.. Nêu nhận xét.
Bài 5 Thực hiện các phép chia sau:
Bài 5 Thực hiện các phép chia sau:
Bài 6 Tìm nghịch đảo của z là:
a) z = 1 + 2i
b) z = - 3i
c) z = i
d) z = 5 + i
Bài 7 Thực hiện các phép tính sau:
Bài 8 Giải các phương trình sau:
Bài 9 Số phức 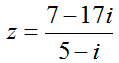
Bài 10 Nghịch đảo của số phức z = 1 + i là?
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.