Toptailieu.vn biên soạn và giới thiệu Chuyên đề Mặt cầu gồm đầy đủ các phần: Lý thuyết, phương pháp giải, bài tập minh họa có lời giải chi tiết giúp học sinh làm tốt bài tập Toán 12 từ đó học tốt môn Toán. Mời các bạn đón xem:
Mặt cầu: Lý thuyết, cách giải và bài tập hay, chi tiết
A. Lý thuyết.
I. cầu và các khái niệm liên quan đến mặt cầu.
1. Mặt cầu
- Tập hợp những điểm M trong không gian cách điểm O cố định một khoảng không đổi bằng r (r > 0) được gọi là mặt cầu tâm O, bán kính r.
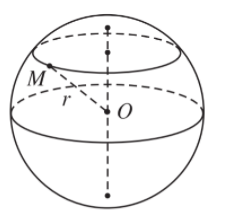
Ta kí hiệu mặt cầu tâm O, bán kính r là S(O; r) hay viết tắt là (S). Như vậy ta có mặt cầu S(O; r) = {M| OM = r}.
- Nếu hai điểm C; D nằm trên mặt cầu S(O; r) thì đoạn thẳng CD được gọi là dây cung của mặt cầu đó.
- Dây cung AB đi qua tâm O được gọi là một đường kính của mặt cầu. Khi đó, độ dài đường kính bằng 2r.
- Một mặt cầu được xác định nếu biết tâm và bán kính của nó hoặc biết một đường kính của mặt cầu đó.
Ví dụ 1. Cho tứ diện ABCD có O là trung điểm của đoạn thẳng nối trung điểm của hai cạnh đối diện. Tìm tập hợp các điểm M trong không gian thỏa mãn hệ thức (với a > 0 không đổi).
Lời giải:
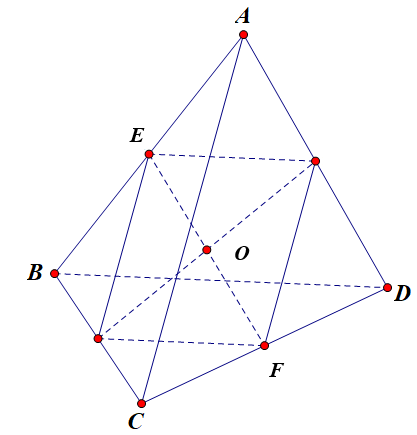
Gọi E; F lần lượt là trung điểm của các cạnh AB và CD.
Suy ra O là trung điểm của EF.
Ta có:
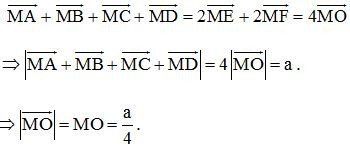
Vậy tập hợp các điểm M cần tìm trong không gian là mặt cầu tâm O bán kính .
2. Điểm nằm trong và nằm ngoài mặt cầu. Khối cầu.
Cho mặt cầu tâm O bán kính r và A là một điểm bất kì trong không gian.
- Nếu OA = r thì ta nói điểm A nằm trên mặt cầu S(O; r).
- Nếu OA < r thì ta nói điểm A nằm trong mặt cầu S(O; r).
- Nếu OA > r thì ta nói điểm A nằm ngoài mặt cầu S(O; r).
Tập hợp các điểm thuộc mặt cầu S(O; r) cùng với các điểm nằm trong mặt cầu đó được gọi là khối cầu hoặc hình cầu tâm O, bán kính r.
3. Biểu diễn mặt cầu.
- Ta thường dùng phép chiếu vuông góc lên mặt phẳng để biểu diễn mặt cầu. Khi đó, hình biểu diễn của mặt cầu là một hình tròn.
- Muốn cho hình biểu diễn của mặt cầu được trực quan ta thường vẽ thêm hình biểu diễn của một số đường tròn nằm trên mặt cầu đó.
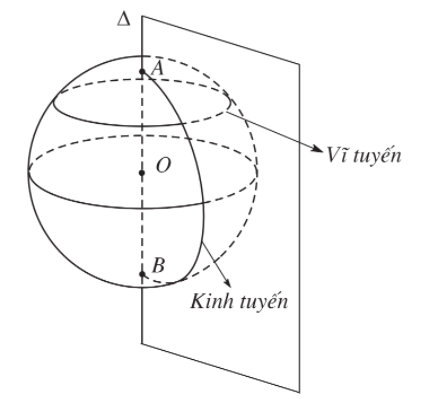
4. Đường kinh tuyến và vĩ tuyến của mặt cầu.
Ta có thể xem mặt cầu như là mặt tròn xoay được tạo nên bởi một nửa đường tròn quay quanh trục chứa đường kính của nửa đường tròn đó. Khi đó, giao tuyến của mặt cầu với các nửa mặt phẳng có bờ là trục của mặt cầu được gọi là kinh tuyến của mặt cầu, giao tuyến (nếu có) của mặt cầu với các mặt phẳng vuông góc với trục được gọi là vĩ tuyến của mặt cầu. Hai giao điểm của mặt cầu với trục được gọi là hai cực của mặt cầu.
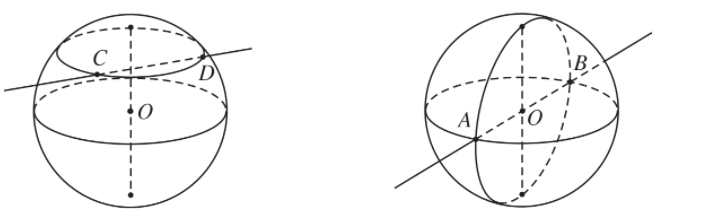
II. Giao của mặt cầu và mặt phẳng
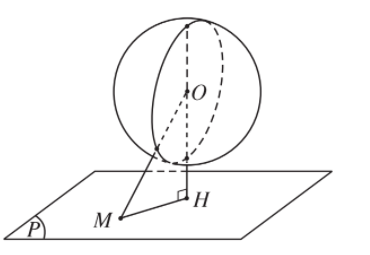
Cho mặt cầu S(O; r) và mặt phẳng (P). Gọi H là hình chiếu vuông góc của O lên mặt phẳng (P). Khi đó h = OH là khoảng cách từ O tới mặt phẳng (P). Ta có ba trường hợp sau:
1. Trường hợp h > r.
Nếu M là một điểm bất kì trên mặt phẳng (P) thì OM ≥ OH. Từ đó suy ra OM > r.
Vậy mọi điểm M thuộc mặt phẳng (P) đều nằm ngoài mặt cầu.
Do đó, mặt phẳng (P) không có điểm chung với mặt cầu.
2. Trường hợp h = r.
- Trong trường hợp này điểm H thuộc mặt cầu S (O; r). Khi đí, với mọi điểm M thuộc mp(P) nhưng khác với H ta luôn có:
OM > OH = r nên OM > r.
Như vậy, H là điểm chung duy nhất của mặt cầu S(O; r) và mặt phẳng (P). Khi đó ta nói mặt phẳng (P) tiếp xúc với mặt cầu S(O; r) tại H.
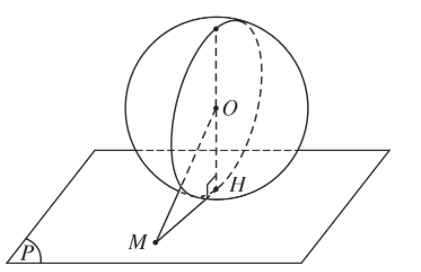
- Điểm H gọi là tiếp điểm của mặt cầu S(O; r) và mặt phẳng (P), mp(P) gọi là mặt phẳng tiếp xúc hay tiếp diện của mặt cầu. Vậy ta có:
- Điều kiện cần và đủ để mặt phẳng (P) tiếp xúc với mặt cầu S(O; r) tại điểm H là (P) vuông góc với bán kính OH tại điểm H đó.
3. Trường hợp h < r.
- Trong trường hợp này mặt phẳng cắt mặt cầu theo đường tròn tâm H; bán kính .
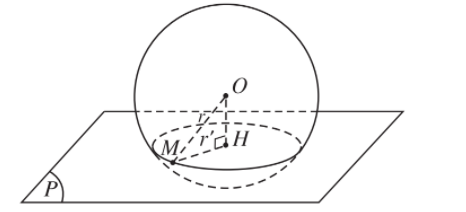
- Đặc biệt khi h = 0 thì tâm O của mặt cầu thuộc mặt phẳng (P). Ta có giao tuyến của mặt phẳng (P) và mặt cầu S(O; r) là đường tròn tâm O bán kính r. Đường tròn này gọi là đường tròn lớn.
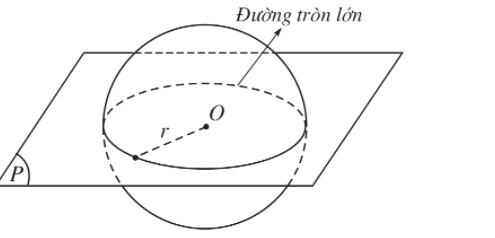
Mặt phẳng đi qua tâm O của mặt cầu được gọi là mặt phẳng kính của mặt cầu đó.
III. Giao của mặt cầu với đường thẳng.Tiếp tuyến của mặt cầu.
Cho mặt cầu S(O; r) và đường thẳng ∆.
Gọi H là hình chiếu vuông góc của tâm O trên ∆ và d = OH là khoảng cách từ O đến ∆.
1. Nếu d > r thì ∆ không cắt mặt cầu S(O; r), vì với mọi điểm M thuộc ∆ ta đều có OM > r và như vậy mọi điểm M thuộc ∆ đều nằm ngoài mặt cầu.
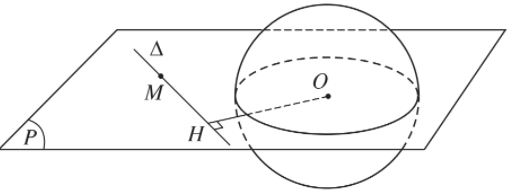
2. Nếu d = r thì mọi điểm H thuộc mặt cầu S(O; r). Khi đó, với mọi điểm M thuộc ∆ nhưng khác H ta luôn có: OM > OH = r nên OM > r.
- Như vậy H là điểm chung duy nhất của mặt cầu S(O; r) và đường thẳng ∆. Khi đó, ta nói đường thẳng ∆ tiếp xúc với mặt cầu S(O; r) tại H.
Điểm H gọi là tiếp điểm của ∆ và mặt cầu. Đường thẳng ∆ gọi là tiếp tuyến của mặt cầu.
- Vậy: Điều kiện cần và đủ để đường thẳng ∆ tiếp xúc với mặt cầu S(O; r) tại điểm H là ∆ vuông góc với bán kính OH tại điểm H.
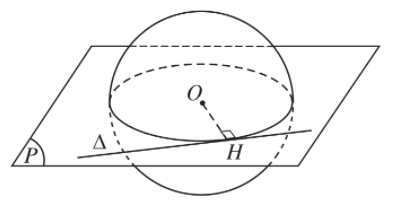
3. Nếu d < r thì đường thẳng ∆ cắt mặt cầu S(O; r) tại hai điểm M; N phân biệt. Hai điểm đó chính là giao điểm của đường thẳng ∆ với đường tròn giao tuyến của mặt cầu S(O; r) và mặt phẳng (O; ∆).
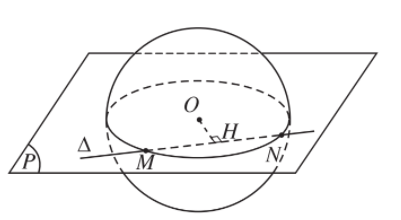
- Đặc biệt, khi d = 0 thì đường thẳng ∆ đi qua tâm O và căt mặt cầu tại hai điểm A; B. Khi đó, AB là đường kính của mặt cầu.
- Nhận xét:
a) Qua một điểm A nằm ngoài mặt cầu S(O; r) có vô số tiếp tuyến của mặt cầu đó. Tất cả các tiếp tuyến này đều vuông góc với bán kính OA của mặt cầu tại A và đều nằm trên mặt phẳng tiếp xúc với mặt cầu tại điểm A.
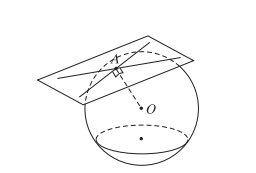
b) Qua một điểm A nằm ngoài mặt cầu S(O; r) có vô số tiếp tuyến với mặt cầu đã cho. Các tiếp tuyến này tạo thành một mặt nón đỉnh A. Khi đó độ dài các đoạn thẳng kẻ từ A đến các tiếp điểm đều bằng nhau.
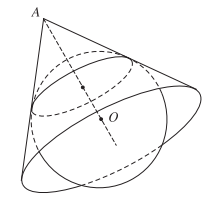
- Chú ý: Người ta nói mặt cầu nội tiếp hình đa diện nếu mặt cầu đó tiếp xúc với tất cả các mặt của hình đa diện, còn nói mặt cầu ngoại tiếp hình đa diện nếu tất cả các đỉnh của hình đa diện đều nằm trên mặt cầu.
Khi mặt cầu nội tiếp (ngoại tiếp) hình đa diện, người ta cũng nói hình đa diện ngoại tiếp (nội tiếp) mặt cầu.
IV. Công thức tính diện tích mặt cầu và thể tích khối cầu.
- Mặt cầu bán kính r có diện tích là: .
- Khối cầu bán kính r có thể tích là: .
- Chú ý:
a) Diện tích S của mặt cầu bán kính r bằng bốn lần diện tích hình tròn lớn của mặt cầu đó.
b) Thể tích V của khối cầu bán kính r bằng thể tích khối chóp có diện tích đáy bằng diện tích mặt cầu và có chiều cao bằng bán kính của khối cầu đó.
- Ví dụ 2. Cho hình tròn đường kính 4a quay quanh đường kính của nó. Khi đó thể tích khối tròn xoay sinh ra bằng bao nhiêu?
Lời giải:
Cho hình tròn đường kính 4a quay quanh đường kính của nó ta được khối cầu có đường kính 4a hay bán kính R = 2a.
Thể tích khối cầu là:
B. Bài tập
I. Bài tập trắc nghiệm
Câu 1: Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Bán kính mặt cầu ngoại tiếp hình lập phương là:
Lời giải:
Ta có:
Ta nhận thấy tâm I của mặt cầu ngoại tiếp hình lập phương chính là tâm của hình lập phương đó. Do đó I chính là trung điểm của AC’ và mặt cầu ngoại tiếp hình lập phương có bán kính là
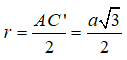
Đáp án đúng là C.
Câu 2: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 1, mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích V của khối cầu ngoại tiếp hình chóp đã cho.
Lời giải:
Câu 3: Tính bán kính của mặt cầu ngoại tiếp hình chóp tam giác đều S,ABC , biết các cạnh đáy có độ dài bằng a , cạnh bên SA = a .
Lời giải:
Câu 4: Một hình lăng trụ tam giác đều có cạnh đáy bằng a, cạnh bên bằng 2a. Tính bán kính mặt cầu ngoại tiếp hình lăng trụ đó.
Lời giải:
Cho lăng trụ tam giác đều ABC.A'B'C' .
Gọi G, G; lần lượt là tâm của hai đáy ABC và A'B'C' .
Ta có GG' chính là trục của các tam giác ABC và A'B'C' .
Gọi O là trung điểm của GG' thì O cách đều 6 đỉnh của hình lăng trụ
nên là tâm của mặt cầu ngoại tiếp hình lăng trụ. Bán kính mặt cầu là R = OA .
Xét tam giác OAG vuông tại G , ta có:
Câu 5: Cho mặt cầu tâm O bán kính R và điểm A bất kì trong không gian. Điểm A không nằm ngoài mặt cầu khi và chỉ khi:
A. OA = R
B. OA ≤ R
C. OA < R
D. OA > R
Lời giải:
Đáp án đúng là B.
Câu 6: Cho hình chóp S.ABC có đáy là tam giác vuôg cân đỉnh B và BC = a, SA ⊥ (ABC), SA = 2a. Khẳng định nào sau đây là đúng?
A. Điểm S nằm trong mặt cầu tâm A bán kính a
B. Điểm S nằm ngoài mặt cầu tâm A bán kính 2a
C. Điểm C nằm trong mặt cầu tâm A bán kính 2a
D. Cả ba điểm S, B, C cùng nằm trong mặt cầu tâm A bán kính 2a.
Lời giải:
Từ giả thiết ta có: SA = 2a; AB = a và AC = a .
Đáp án đúng là C.
Câu 7: Cho mặt cầu (S) tâm O bán kính R và một mặt phẳng (P). Kí hiệu h là khoảng cách từ O đến mặt phẳng (P). Mặt phẳng (P) có nhiều hơn một điểm chung với mặt cầu (S) nếu :
A. h ≤ R
B. h ≥ R
C. h > R
D. h < R
Lời giải:
Từ vị trí tương đối của một mặt phẳng với mặt cầu ta có đáp án đúng là D.
Câu 8: Cho mặt cầu (S) tâm O bán kính R và một đường thẳng d. Kí hiệu h là khoảng cách từ O đến đường thẳng d. Đường thẳng d có điểm chung với mặt cầu (S) nếu và chỉ nếu:
A. h ≤ R
B. h = R
C. h > R
D. h < R
Lời giải:
Từ vị trí tương đối của một đường thẳng và mặt cầu ta có đường thẳng d có điểm chung với mặt cầu (S) khi và chỉ khi đường thẳng d tiếp xúc hoặc cắt mặt cầu (S).
Đáp án đúng là A.
Câu 9: Cho hình chóp S.ABCD có đáy ABCD là hình vuông có cạnh bằng 2a, SA vuông góc với đáy và SA = a. Bán kính mặt cầu tâm A tiếp xúc với mặt phẳng (SBC) theo a là:
A. 2a
B. a
C.
D.
Lời giải:
Ta có mặt cầu S(A;r) tiếp xúc với mặt phẳng (SBC) khi và chỉ khi r = d(A; (SBC)) .
Hạ AH ⊥ SB tại H. Do BC ⊥ AB và BC ⊥ SA nên BC ⊥ (SAB) , suy ra BC ⊥ AH .
Mặt khác AH ⊥ SB nên AH ⊥ (SBC) hay d(A; (SBC)) = AH Xét tam giác vuông SAB ta có:
Đáp án đúng là D.
Câu 10: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = 2AD = 2a. SA vuông góc với đáy, góc giữa cạnh bên SB và đáy là 45o . Bán kính mặt cầu tâm A cắt mặt phẳng (SBD) theo một đường tròn có bán kính bằng a là:
Lời giải:
Ta có mặt cầu S(A;r) cắt mặt phẳng (SBD) theo một đường tròn có bán kính bằng a khi và chỉ khi ta có
Ta có:
Hạ AK ⊥ BD tại K, hạ AH ⊥ SK tại H. Do BD ⊥ AK và BD ⊥ SA nên BD ⊥ (SAK) , suy ra BD ⊥ AH. Mặt khác AH ⊥ SK nên ta có AH ⊥ (SBDB) hay d(A; (SBD)) = AH. Xét tam giác vuông SAK và tam giác vuông ABD ta có:
Khi đó ta có:
Đáp án đúng là C.
II. Bài tập tự luận có lời giải
Câu 1: Cho hình chóp S.ABCD có đáy ABCD là hình vuông có cạnh bằng a, SA vuông góc với đáy và SA = 2a. Bán kính mặt cầu tâm A tiếp xúc với SC theo a là :
Lời giải:
Ta có mặt cầu S(A ;r) tiếp xúc với đường thẳng SC khi và chỉ khi ta có r = d(A; SC).
Xét tam giác vuông ABC ta có AC = a . Hạ AH ⊥ SC tại H. Xét tam giác vuông SAC ta có :
Câu 2: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA = AB = 2AD = 2a. Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với đáy. Bán kính mặt cầu tâm B cắt SC theo một dây có độ dài 2a là?
Lời giải:
Do (SAB) ⊥ (ABCD) và (SAD) ⊥ (ABCD) ta có SA ⊥ (ABCD). Theo định lí ba đường vuông góc ta có BC ⊥ SB .
Hạ BH ⊥ SC tại H. Xét tam giác vuông SBC ta có:
Ta có mặt cầu S(B;r) cắt đường thẳng SC theo một dây cung có độ dài 2a khi và chỉ khi ta có
Câu 3: Cho hai quả cầu cùng bán kính là 5cm. Để đựng hai quả cầu Nam phải làm một hình hộp chữ nhật từ bìa carton. Hỏi trong các đáp án dưới đây, Nam cần ít nhất bao nhiêu xen-ti-mét vuông bìa carton để làm được chiếc hộp đó?
Lời giải:
Hình hộp chữ nhật đựng được hai quả cầu bán kính 5cm thì độ dài các cạnh ít nhất là 10cm, 10cm, 20cm. Khi đó ta có: Stp = 2 x 102 + 4 x 10 x 20 = 1000(cm2) .
Câu 4: Trong các mệnh đề sau, mệnh đề nào sai?
-Hình chóp có mặt cầu ngoại tiếp khi và chỉ khi hình chóp có đáy là một tứ giác nội tiếp được đường tròn.
-Hình chóp có mặt cầu ngoại tiếp nếu nó là hình chóp tam giác
-Hình chóp có mặt cầu ngoại tiếp nếu nó có các cạnh bên bằng nhau.
-Hình chóp có mặt cầu ngoại tiếp nếu có cạnh bên vuông góc với đáy.
Lời giải:
Hình chóp có mặt cầu ngoại tiếp khi và chỉ khi hình chóp đó có đáy là một đa giác nội tiếp được đường tròn nên mệnh đề A và B đúng. Hình chps có các cạnh bên bằng nhau có hình chiếu vuông góc của đỉnh lên mặt đáy là tâm đường tròn ngoại tiếp đáy nên hình chóp đó có đáy nội tiếp được đường tròn
Câu 5: Trong các mệnh đề sau, mệnh đề nào đúng?
- Hình lăng trụ có mặtc ầu ngoại tiếp nếu đáy của nó là hình vuông
-Hình lăng trụ có mặt cầu ngoại tiếp nếu nó là lăng trụ đứng
- Hình lăng trụ có mặt cầu ngoại tiếp nếu nó có đáy là đa giác nội tiếp được đường tròn
- Hình lăng trụ có mặt cầu ngoại tiếp nếu nó là lăng trụ đứng tam giác.
Lời giải:
Đáp án đúng là 4
Câu 6: Cho hình chóp S.ABCD có đáy ABCD là hình vuông có cạnh bằng a, SA vuông góc với đáy và SA = a. Bán kính mặt cầu ngoại tiếp hình chóp là:
Lời giải:
Theo định lí ba đường vuông góc ta có tam giác SBC, SDC lần lượt vuông tại B, D. Gọi I là trung điểm của SC. Từ các tam giác SAC, SBC, SDC vuông ta có:
Vậy I là tâm mặt cầu ngoại tiếp hình chóp S.ABCD và bán kính mặt cầu là
Câu 7: Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông cân tại A, BC = a và góc giữa A’B và mặt phẳng (ABC) là 60o . Bán kính của mặt cầu ngoại tiếp lăng trụ là :
Lời giải:
Trong tam giác vuông ABC ta có
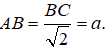
=> AA' = AB.tan60o = a
Gọi I là tâm của hình chữ nhật BCC’B’ và M là trung điểm của BC. Do tam giác ABC vuông tại A nên M là tâm đường tròn ngoại tiếp tam giác ABC và do đó IM là trục của đường tròn ngoại tiếp đáy ABC và I cách đều B, B’ nên I là tâm của mặt cầu ngoại tiếp lăng trụ. Khi đó ta có :
Câu 8: Tính bán kính của mặt cầu ngoại tiếp hình chóp tứ giác đều có cạnh đáy bằng a, cạnh bên bằng 2a.
Lời giải:
Cho hình chóp tứ giác đều S.ABCD.
Gọi H là tâm đáy
thì SH là trục của hình vuông .
Gọi M là trung điểm của ABCD .
Trong mp (SDH) kẻ trung trực của đoạn SD cắt SH tại O
Thì OS = OA = OC = OD
Nên O chính là tâm của mặt cầu ngoại tiếp hình chóp S.ABCD .
Bán kính mặt cầu là R = SO .
Ta có :
Câu 9: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân đỉnh A và AB = SB = a , SB vuông góc với mặt phẳng (ABC). Bán kính nhỏ nhất của mặt cầu tiếp xúc với đường thẳng SC và AB là?
Lời giải:
Mặt cầu S(I,r) tiếp xúc với AB, SC lần lượt tại T, K. Khi đó ta có:
2r = IT + IK ≥ d(AB; SC) => r ≥
Dựng hình bình hành ABDC, khi đó ta có ABDC là hình vuông cạnh a. Hạ BH vuông góc với SD tại H. Khi đó ta có BH ⊥ (SCD).
Suy ra: d(SC; AB) = d(AB, (SCD)) = d(B; (SCD))
Câu 10: Cho đường thẳng a và điểm A cách đường thẳng a một khoảng bằng 4cm. Trong các mặt cầu đi qua A và tiếp xúc với đường thẳng a, mặt cầu (S) có diện tích nhỏ nhất thì diện tích đó bằng?
Lời giải:
Gọi S(I ;r) là mặt cầu đi qua A và tiếp xúc với a.
Ta có diện tích của mặt cầu là : S = 4πr3 nên S đạt giá trị nhỏ nhất khi và chỉ khi r đạt giá trị nhỏ nhất.
Gọi tiếp điểm của đường thẳng a và mặt cầu là H và hình chiếu vuông góc hạ từ A lên đường thẳng A là A’. Khi đó ta có :
2r = IA + IH ≥ AH ≥ AA' => r ≥ = 2(cm)
Vậy r đạt giá trị nhỏ nhất bằng 2cm khi I là trung điểm của AA’.
Khi đó mặt cầu (S) có diện tích nhỏ nhất là S = 4π22 = 16π(cm2).
III. Bài tập vận dụng
Bài 1 Cho mặt cầu (S) tâm O bán kính R và một mặt phẳng (P). Kí hiệu h là khoảng cách từ O đến mặt phẳng (P). Mặt phẳng (P) và mặt cầu (S) có điểm chung nếu và chỉ nếu?
Bài 2 Trong không gian cho đường thẳng Δ và điểm O cách Δ một khoảng bằng 20cm. Mặt cầu (S) tâm O cắt đường thẳng Δ theo một dây có độ dài 30cm có bán kính r bằng?
Bài 3 Cho hình chóp tam giác đều S.ABC có SA tạo với đáy một góc bằng 30o và SA=2a. Trong các điểm S, B, C điểm nào nằm trong mặt cầu tâm A bán kính 3a.
Bài 4 Cho hình chóp S.ABCD có đáy ABCD là hình vuông có cạnh bằng 2a, SAB là tam giác đều. Bán kính mặt cầu tâm A cắt SB theo một dây có độ dài a là?
Bài 5 Cho đường tròn (C) ngoại tiếp một tam giác đều ABC có cạnh bằng a, chiều cao AH. Quay đường tròn (C) xung quanh trục AH , ta được một mặt cầu. Thể tích của khối cầu tương ứng là?
Bài 6 Cho tam giác ABC vuông tại A có BC = 2a và ^ = 30° . Quay tam giác vuông này quanh trục AB , ta được một hình nón đỉnh B . Gọi S1 là diện tích toàn phần của hình nón
Bài 7 đó và S2 là diện tích mặt cầu có đường kính AB . Khi đó, tỉ số 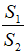
Bài 8 Tính bán kính của mặt cầu ngoại tiếp hình tứ diện đều cạnh a.
Bài 9 Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có AB = 2AD = 2a, SA vuông góc với đáy, SA = a. Bán kính mặt cầu ngoại tiếp hình chóp là?
Bài 10 Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt đáy và SA = a.Tính diện tích mặt cầu ngoại tiếp hình chóp S.ABC .
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.