Toptailieu.vn biên soạn và giới thiệu Công thức giải bất phương trình lôgarit hay, chi tiết, từ cơ bản đến nâng cao giúp học sinh nắm vững kiến thức về Công thức giải bất phương trình lôgarit, từ đó học tốt môn Toán.

Công thức giải bất phương trình lôgarit chi tiết

1. Bất phương trình lôgarit cơ bản

- Bất phương trình lôgarit cơ bản có dạng logax>b (hoặc logax≥b, logax<b, logax≤b) với a>0, a≠1.

2. Tập nghiệm của bất phương trình lôgarit cơ bản.

a. Nghiệm của bất phương trình logax>b, (a>0, a≠1)

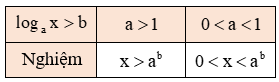
b. Tập nghiệm của bất phương trình ${\log }_{a}x\ge b,\left(a>0,a\ne 1\right)$

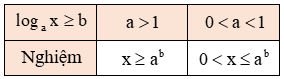
c. Tập nghiệm của bất phương trình ${\log }_{a}x<b,\left(a>0,a\ne 1\right)$

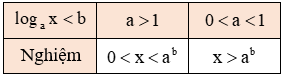
d. Tập nghiệm của bất phương trình ${\log }_{a}x\le b,\left(a>0,a\ne 1\right)$

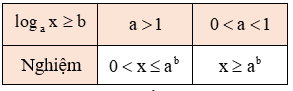
- Chú ý: Khi giải bất phương trình lôgarit ta cần tìm điều kiện của x.

3. Một số bất phương trình lôgarit đơn giản

VD1. Giải các bất phương trình sau:

a. ${\log }_{0,5}\left(5x+10\right)<{\log }_{0,5}\left(x^2+6x+8\right)$

b. ${\log }_{\frac{1}{2}}\left(x^2+2x-8\right)\ge -4$

c. ${\log }_3\left[{\log }_{\frac{1}{2}}\left(x^2-1\right)\right]<1$

Lời giải:

a. ${\log }_{0,5}\left(5x+10\right)<{\log }_{0,5}\left(x^2+6x+8\right)$

Điều kiện:

$\left\{\begin{array}{l}5x+10>0\\ x^2+6x+8>0\end{array}\right.\iff x>-2$

Bất phương trình $\iff 5x+10>x^2+6x+8$

(Vì $0,5<1$)

$\iff x^2+x-2<0\iff -2<x<1$

Kết hợp với điều kiện ta được $-2<x<1$

Vậy bất phương trình có tập nghiệm là $S=\left(-2;1\right)$

b.

${\log }_{\frac{1}{2}}\left(x^2+2x-8\right)\ge -4$

Điều kiện:

$x^2+2x-8>0\iff \left[\begin{array}{l}x>2\\ x<-4\end{array}\right.$

Bất phương trình:

$$\begin{gathered} \iff x^2+2x-8\le {\left(\frac{1}{2}\right)}^{-4} \\ \iff x^2+2x-8\le 16 \end{gathered}$$

$$\begin{gathered} \iff x^2+2x-24\le 0 \\ \iff -6\le x\le 4 \end{gathered}$$

Kết hợp với điều kiện ta được tập nghiệm là $S=\left[-6;-4\right)\cup \left(2;4\right]$

c. 

${\log }_3\left[{\log }_{\frac{1}{2}}\left(x^2-1\right)\right]<1$

Điều kiện:

$$\begin{gathered} {\log }_{\frac{1}{2}}\left(x^2-1\right)>0\iff x^2-1<1 \\ \iff -\sqrt{2}<x<\sqrt{2} \end{gathered}$$

Bất phương trình:

$\iff {\log }_{\frac{1}{2}}\left(x^2-1\right)<3$

$$\begin{gathered} \iff x^2-1>\frac{1}{8}\iff x^2>\frac{9}{8} \\ \iff \left[\begin{array}{l}x>\frac{3\sqrt{2}}{4}\\ x<-\frac{3\sqrt{2}}{4}\end{array}\right. \end{gathered}$$

Kết hợp với điều kiện ta được tập nghiệm là:

$S=\left(-\sqrt{2};-\frac{3\sqrt{2}}{4}\right)\cup \left(\frac{3\sqrt{2}}{4};\sqrt{2}\right)$

VD2. Giải các bất phương trình sau:

a. ${\log }_2\left(x-3\right)+{\log }_2\left(x-2\right)>1$

b. ${\log }_{\sqrt{3}}\left(x-3\right)-{\log }_3\left(x^2-2x+3\right)\le 1$

c. ${\log }_{0,2}x-{\log }_5\left(x-2\right)<{\log }_{0,2}3$

Lời giải:

a.

b.

c.

VD3. Giải các bất phương trình sau:

a. ${\log }_3^{2}x-5{\log }_{3}x+6\le 0$

b. $\frac{1}{5-\log x}+\frac{2}{1+\log x}<1$

c. $4{\log }_{4}x-33{\log }_{x}4\le 1$

Lời giải:

a.

b.

Bảng xét dấu:

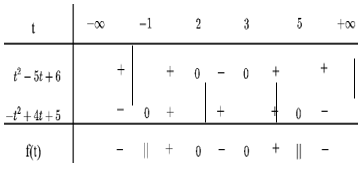
Dựa vào bảng xét dấu ta thấy:

VD4. Giải bất phương trình: ${\log }_{\frac{1}{3}}x>3x$                                 

Lời giải:

${\log }_{\frac{1}{3}}x>3x$

Điều kiện: x >0

Xét hàm số $f\left(x\right)={\log }_{\frac{1}{3}}x-3x$

Ta có:

$f\text{'}\left(x\right)=\frac{1}{x.\ln \frac{1}{3}}-3<0\forall x>0$

$\Rightarrow f\left(x\right)$ nghịch biến

Do vậy với $x<\frac{1}{3}\Rightarrow f\left(x\right)>f\left(\frac{1}{3}\right)=0$

Vậy bất phương trình có tập nghiệm là $S=\left(-\infty ;\frac{1}{3}\right)$

4. Luyện tập

Bài 1. Giải các bất phương trình sau:

a. ${\log }_8\left(4-2x\right)\ge 2$

b. ${\log }_{\frac{1}{3}}\left(3x+2\right)<{\log }_{\frac{1}{3}}\left(x-2\right)$

c. ${\log }_2\left(x^2-2x\right)>3$

Bài 2. Giải các bất phương trình sau:

a. ${\log }_2\left(2-x-\sqrt{x^2-1}\right)<1$

b. ${\log }_{\sqrt{5}}\left(6^{x+1}-{36}^x\right)\le 2$

Bài 3. Giải các bất phương trình sau:

a. ${\log }_{0,2}^{2}x-5{\log }_{0,2}x<-6$

b. $\frac{1}{3-{\log }_{2}x}+\frac{3}{1+{\log }_{2}x}>2$

c. ${\log }_{\frac{1}{5}}\left(x^2-6x+18\right)+2{\log }_5\left(x-4\right)<0$

Bài 4. Giải các bất phương trình sau:

a. ${\log }_{\frac{1}{3}}\left[{\log }_2{x}^2\right]>0$

b. ${\log }_{2}x\le 6-x$