Toptailieu.vn biên soạn và giới thiệu Công thức nguyên hàm hữu tỉ hay, chi tiết, từ cơ bản đến nâng cao giúp học sinh nắm vững kiến thức về Công thức nguyên hàm hữu tỉ, từ đó học tốt môn Toán.
Công thức nguyên hàm hữu tỉ đầy đủ, chi tiết
1. Lý thuyết
Bài toán tổng quát: Tính nguyên hàm với P(x) và Q(x) là các đa thức.
Phương pháp giải:
Nếu bậc của tử số P(x) lớn hơn hoặc bằng bậc của mẫu số Q(x) thì chia đa thức.
Nếu bậc của tử số P(x) nhỏ hơn bậc của mẫu số Q(x) thì xem xét mẫu số và khi đó:
- Nếu mẫu số phân tích được thành tích số, ta sẽ sử dụng đồng nhất thức để đưa về dạng tổng của các phân số.
Một số trường hợp đồng nhất thức thường gặp:
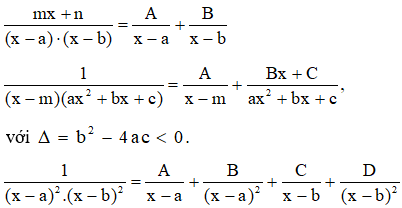
Nếu mẫu số không phân tích được thành tích số (biến đổi và đưa về dạng lượng giác).
2. Ví dụ minh họa
Ví dụ 1: Tính các nguyên hàm sau:
a)
b)
c)
Lời giải
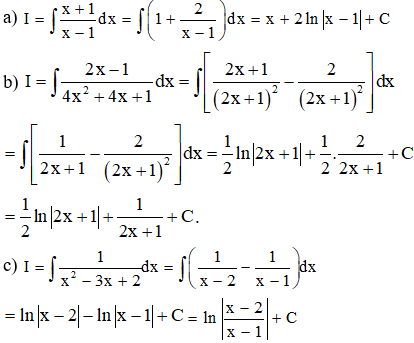
Ví dụ 2: Tính các nguyên hàm sau:
a)
b)
Lời giải
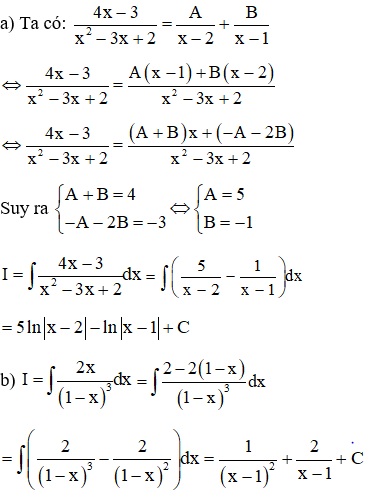
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.