Toptailieu.vn biên soạn và giới thiệu Công thức nguyên hàm hàm logarit hay, chi tiết, từ cơ bản đến nâng cao giúp học sinh nắm vững kiến thức về Công thức nguyên hàm hàm logarit , từ đó học tốt môn Toán.
Công thức nguyên hàm hàm logarit đầy đủ, chi tiết
1. Lý thuyết
Nguyên hàm chứa lnf(x), ta thường làm theo phương pháp đổi biến số hoặc phương pháp nguyên hàm từng phần.
a) Một số dạng hàm số chứa ln sử dụng phương pháp đổi biến số thường gặp:
b) Các dạng chứa lnf(x) mà không chứa , ta sử dụng nguyên hàm từng phần
Công thức nguyên hàm từng phần:
Phương pháp giải:
Bước 1: Đặt u là biểu thức chứa lnf(x), dv là phần còn lại
Bước 2: Tính du và v
Bước 3: Áp dụng công thức nguyên hàm từng phần.
2. Ví dụ minh họa
Ví dụ 1: Tính các nguyên hàm sau:
a)
b)
Lời giải
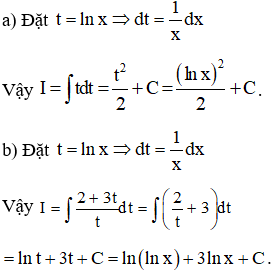
Ví dụ 2: Tính các nguyên hàm sau:
a)
b)
Lời giải
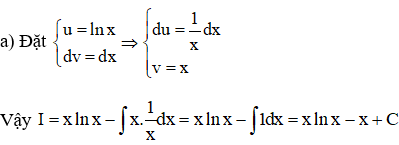
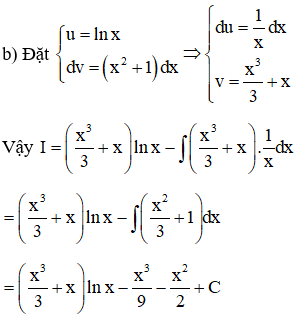
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.
