Toptailieu.vn biên soạn và giới thiệu Công thứcvề tỉ số thể tích khối đa diện hay, chi tiết, từ cơ bản đến nâng cao giúp học sinh nắm vững kiến thức về Công thứcvề tỉ số thể tích khối đa diện, từ đó học tốt môn Toán.

Công thức về tỉ số thể tích khối đa diện đầy đủ, chi tiết

1. Tỉ số thể tích khối lăng trụ tam giác

Bài toán: Cho khối lăng trụ tam giác ABC.A’B’C’. Trên các cạnh AA’, BB’, CC’ lần lượt lấy các điểm M, N, P. Tính thể tích hình đa diện ABC.MNP

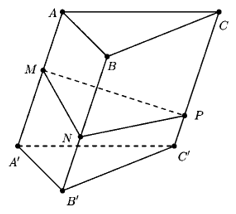
Ta đặt các tỉ số:

$\frac{AM}{AA\text{'}}=a$; $\frac{BN}{BB\text{'}}=b$;$\frac{CP}{CC\text{'}}=c$

Khi đó ta có tỉ số thể tích:

$\frac{V_{ABC.MNP}}{V_{ABC.A\text{'}B\text{'}C\text{'}}}=\frac{a+b+c}{3}$

VD1. Cho lăng trụ ABC.A’B’C’ có thể tích bằng 27. Gọi M, N lần lượt là trung điểm của AA’ và BB’. Tính thể tích của khối đa diện CNMA’B’C’.

Lời giải:

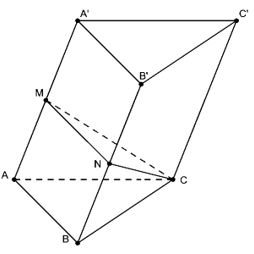
Ta tính các tỉ số: $\frac{A\text{'}M}{A\text{'}A}=\frac{B\text{'}N}{B\text{'}B}=\frac{1}{2}$

Sử dụng công thức tỉ số thể tích ta có:

$$\begin{gathered} \frac{V_{A\text{'}B\text{'}C\text{'}.MNC}}{V_{A\text{'}B\text{'}C\text{'}.ABC}}=\frac{\frac{1}{2}+\frac{1}{2}+1}{3}=\frac{2}{3} \\ \Rightarrow V_{A\text{'}B\text{'}C\text{'}.MNC}=\frac{2}{3}.27=18 \end{gathered}$$

VD2. Cho khối lăng trụ ABC.A’B’C’ có thể tích V. Các điểm M, N lần lượt thuộc các cạnh BB’, CC’ sao cho $\frac{MB}{BB\text{'}}=\frac{1}{2}$ và $\frac{NC}{CC\text{'}}=\frac{1}{4}$. Thể tích của khối chóp A.BMNC theo V là?

Lời giải:

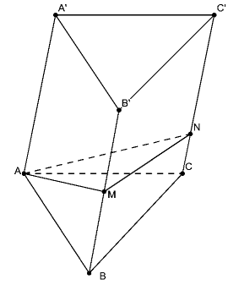
Theo công thức thể tích ta có:

$$\begin{gathered} \frac{V_{A.BMNC}}{V_{ABC.A\text{'}B\text{'}C\text{'}}} \\ =\frac{\frac{AA}{AA\text{'}}+\frac{BM}{BB\text{'}}+\frac{CN}{CC\text{'}}}{3} \\ =\frac{0+\frac{1}{2}+\frac{1}{4}}{3}=\frac{1}{4} \end{gathered}$$

Suy ra $V_{A.BMNC}=\frac{V}{4}$

2. Tỉ số thể tích khối lăng trụ tứ giác

Bài toán: Cho khối hộp ABCD.A’B’C’D’. Trên các cạnh AA’, BB’, CC’, DD’ lấy lần lượt các điểm M, N, P, Q sao cho 4 điểm đồng phẳng. Tính $V_{ABCD.MNPQ}$

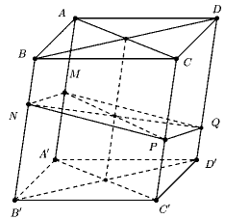
Ta đặt các tỉ số:

$$\begin{gathered} \left.\begin{array}{l}\frac{AM}{AA\text{'}}=a;\frac{BN}{BB\text{'}}=b\\ \frac{CP}{CC\text{'}}=c;\frac{DQ}{DD\text{'}}=d\end{array}\right\} \\ \Rightarrow \frac{V_{ABCD.MNPQ}}{V_{ABCD.A\text{'}B\text{'}C\text{'}D\text{'}}} \\ =\frac{a+b+c+d}{4} \end{gathered}$$

VD1. Cho hình lập phương ABCD.A’B’C’D’ cạnh 2a. Gọi M là trung điểm của BB’ và P là điểm thuộc cạnh DD’ sao cho $DP=\frac{1}{4}DD\text{'}$. Mặt phẳng (AMP) cắt CC’ tại N. Thể tích khối đa diện AMNPBCD bằng?

Lời giải:

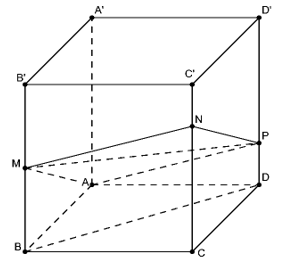
Do AM // (CDD’C’) nên giao tuyến giữa (AMP) và (CDD’C’) là đường thẳng d qua P và song song với AM $\Rightarrow N=d\cap CC\text{'}$. Khi đó PN // AM.

Do 4 điểm A, M, N, P đồng phẳng nên:

$$\begin{gathered} \frac{A\text{'}A}{A\text{'}A}+\frac{C\text{'}N}{C\text{'}C}=\frac{B\text{'}M}{B\text{'}B}+\frac{D\text{'}P}{D\text{'}D} \\ \iff 1+\frac{C\text{'}N}{C\text{'}C}=\frac{1}{2}+\frac{3}{4} \\ \Rightarrow \frac{C\text{'}N}{C\text{'}C}=\frac{1}{4} \end{gathered}$$

Áp dụng công thức tỉ số thể tích ta có:

$$\begin{gathered} \frac{V_{AMNPBCD}}{V_{ABCD.A\text{'}B\text{'}C\text{'}D\text{'}}} \\ =\frac{\frac{AA}{AA\text{'}}+\frac{BM}{BB\text{'}}+\frac{CN}{CC\text{'}}+\frac{DP}{DD\text{'}}}{4} \\ =\frac{0+\frac{1}{2}+\frac{3}{4}+\frac{1}{4}}{4}=\frac{3}{8} \\ \Rightarrow V_{AMNPBCD} \\ =\frac{3}{8}.V_{ABCD.A\text{'}B\text{'}C\text{'}D\text{'}} \\ =\frac{3}{8}.{\left(2a\right)}^3=3a^3 \end{gathered}$$

VD2. Cho hình hộp ABCD.A’B’C’D’ có thể tích là V. Gọi M là điểm thuộc CC’ sao cho $CC\text{'}=3CM$. Mặt phẳng (AB’M) chia khối hộp thành 2 phần. Tính phần thể tích (H) có chứa điểm B.

Lời giải:

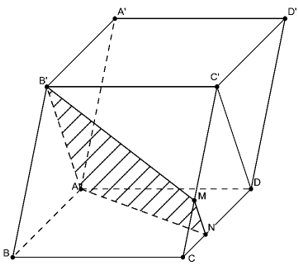
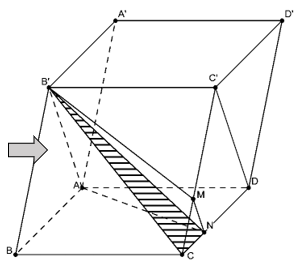
Trong mp (CC’D’D) kẻ MN song song C’D $\Rightarrow \frac{CN}{CD}=\frac{CM}{CC\text{'}}=\frac{1}{3}$

Khi đó phần thể tích cần tính chính là thể tích khối đa diện AB’CMNC.

Ta chia khối đa diện cần tính thành $V_{B\text{'}.ABCN}+V_{B\text{'}.MNC}$

Ta có: $S_{ABCN}=\frac{2}{3}{S}_{ABCD}$

$$\begin{gathered} \Rightarrow V_{B\text{'}.ABCN} \\ =\frac{1}{3}.h.\frac{2}{3}{S}_{ABCD}=\frac{2}{9}V \\ {V}_{B\text{'}.MNC}=V_{B.MNC} \\ =V_{M.BCN}=\frac{1}{3}{V}_{C\text{'}.BCN} \end{gathered}$$

Ta có: $S_{BCN}=\frac{1}{6}{S}_{ABCD}$

$$\begin{gathered} \Rightarrow V_{C\text{'}.BCN} \\ =\frac{1}{3}.h.\frac{1}{6}{S}_{ABCD}=\frac{1}{18}V \end{gathered}$$

Do đó $V_{B\text{'}.MNC}=\frac{1}{54}V$

Vậy $V_{\left(H\right)}=\frac{2}{9}V+\frac{1}{54}V=\frac{13}{54}V$

3. Luyện tập

Bài 1. Cho khối hộp ABCD.A’B’C’D’. Gọi M thuộc cạnh AB sao cho $MB=2MA$.Mặt phẳng (MB’D’) chia khối hộp thành 2 phần. Tính tỉ số thể tích hai phần đó.

Bài 2. Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Gọi M là trung điểm của A’B’, N là trung điểm của BC. Tính thể tích khối tứ diện ADMN.

Bài 3. Cho hình hộp ABCD.A’B’C’D’. Gọi M là điểm thuộc CC’ thỏa mãn $CC\text{'}=4CM$. Mặt phẳng (AB’M) chia khối hộp thành hai phần có thể tích là $V_1$ và $V_2$. Trong đó $V_1$ là thể tích có chứa điểm B. Tính tỉ số $\frac{V_1}{V_2}$

Bài 4. Cho lăng trụ ABC.A’B’C’ có thể tích bằng thể tích khối lập phương cạnh a. Trên các cạnh AA’, BB’ lấy M, N sao cho $\frac{AM}{AA\text{'}}=\frac{BN}{BB\text{'}}=\frac{2}{3}$.

a. Mặt phẳng (CMN) chia khối lăng trụ thành hai phần. Tính tỉ số thể tích hai phần đó.

b. E và F lần lượt là giao điểm của CM với C’A’ và CN với C’B’. Tính thể tích khối chóp C’CEF.

Bài 5. Cho hình lăng trụ ABC.A’B’C’. Gọi M, N, P lần lượt là trung điểm của các cạnh A’B’, BC, CC’. Mặt phẳng (MNP) chia khối lăng trụ thành hai phần. Tính tỉ số thể tích của hai phần đó.

Xem thêm các dạng Toán lớp 12 hay, chi tiết khác:

Công thức tính thể tích khối chóp đầy đủ, chi tiết nhất

Công thức tính thể tích khối lăng trụ đầy đủ, chi tiết nhất

Mặt cầu và phương pháp giải bài tập

Mặt trụ và phương pháp giải bài tập

Mặt nón và phương pháp giải bài tập