Với giải SGK Toán 8 Cánh Diều trang 58 chi tiết trong Bài 1: Hàm số giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 8. Mời các bạn đón xem:

Giải Toán 8 trang 58 Tập 1 (Cánh Diều)

Bài tập

Bài 1 trang 58 Toán 8 Tập 1: Đại lượng y có phải là hàm số của đại lượng x hay không nếu bảng giá trị tương ứng của chúng được cho bởi mỗi trường hợp sau:

a)

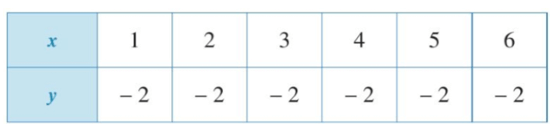
b)

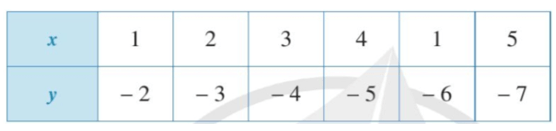
Lời giải:

a)

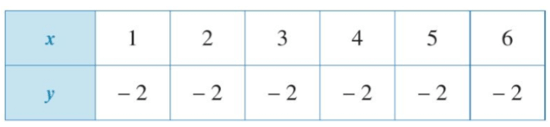
Quan sát bảng trên ta thấy khi x = 1; x = 2; x = 3; x = 4; x = 5; x = 6 thì ta đều xác định  giá trị của y là y = − 2.

Vì mỗi giá trị của x ta chỉ xác định được một giá trị tương ứng của y nên đại lượng y là hàm số của đại lượng x.

b)

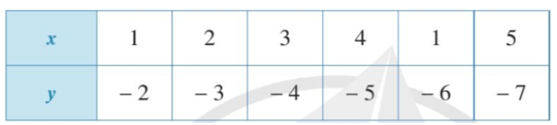
Quan sát bảng trên ta thấy khi x = 1; x = 2; x = 3; x = 4; x = 1; x = 5 thì ta đều xác định  giá trị của y lần lượt là: y = − 2; y = − 3; y = − 4; y = − 5; y = − 6; y = − 7.

Vì mỗi giá trị của x ta chỉ xác định được một giá trị tương ứng của y nên đại lượng y là hàm số của đại lượng x.

Bài 2 trang 58 Toán 8 Tập 1: a) Cho hàm số y = 2x + 10. Tìm giá trị của y tương ứng với mỗi giá trị sau của x:

$x=-5;x=0;x=\frac{1}{2}.$

b) Cho hàm số f(x) = −2x² + 1. Tính $f(-1);f\left(0\right);f\left(\frac{1}{3}\right).$

Lời giải:

a) Thay lần lượt các giá trị $x=-5;x=0;x=\frac{1}{2}$ vào hàm số y = 2x + 10.

• Với x = − 5, ta có: y = 2 . (− 5) + 10 = − 10 + 10 = 0;

• Với x = 0, ta có: y = 2 . 0 + 10 = 0 + 10 = 10;

• Với $x=\frac{1}{2}$, ta có: $y=2.\frac{1}{2}+10=1+10=11$.

Vậy với $x=\frac{1}{2}$ ta xác định được giá trị tương ứng của y lần lượt là y = 0; y = 10; y = 11.

b) Thay lần lượt các giá trị $x=-1;x=0;x=\frac{1}{3}$ vào hàm số f(x) = −2x² + 1.

• f(− 1) = − 2 . (− 1)² + 1 = − 2 . 1 + 1 = − 2  + 1 = − 1;

• f(0) = − 2 . 0² + 1 = 0 + 1 = 1;

• $f\left(\frac{1}{3}\right)=-2.{\left(\frac{1}{3}\right)}^2+1=-2.\frac{1}{9}+1=\frac{-2}{9}+1=\frac{7}{9}$.

Vậy $f(-1)=-1;f\left(0\right)=1;f\left(\frac{1}{3}\right)=\frac{7}{9}$.

Bài 3 trang 58 Toán 8 Tập 1: Cho một thanh kim loại đồng chất có khối lượng riêng là 7,8 g/cm³.

a) Viết công thức tính khối lượng m (g) theo thể tích V (cm³). Hỏi m có phải là hàm số của V hay không? Vì sao?

b) Tính khối lượng của thanh kim loại đó khi biết thể tích của thanh kim loại đó là

V = 1 000 cm³.

Lời giải:

a) Công thức tính khối lượng m (g) theo thể tích V (cm³) là: V = 7,8m.

Suy ra $m=\frac{V}{\mathrm{7,8}}$.

Với mỗi giá trị của V ta xác định được một giá trị của m nên m là hàm số của V.

b) Với V = 1 000 cm³ ta có $m=\frac{1000}{\mathrm{7,8}}=\frac{5000}{39}$ (g).

Vậy khi biết thể tích của thanh kim loại đó là V = 1 000 cm³ thì khối lượng của thanh kim loại đó là $\frac{5000}{39}$ g.

Bài 4 trang 58 Toán 8 Tập 1: Dừa sáp là một trong những đặc sản lạ, quý hiếm và có giá trị dinh dưỡng cao, thường được trồng ở Bến Tre hoặc Trà Vinh. Giá bán mỗi quả dừa sáp là 200 000 đồng.

a) Viết công thức biểu thị số tiền y (đồng) mà người mua phải trả khi mua x (quả) dừa sáp. Hỏi y có phải là hàm số của x hay không? Vì sao?

b) Hãy tính số tiền mà người mua phải trả khi mua 10 quả dừa sáp.

Lời giải:

Giá bán mỗi quả dừa sáp là 200 000 đồng.

a) Công thức biểu thị số tiền y (đồng) mà người mua phải trả khi mua x (quả) dừa sáp là

y = 200 000x (đồng) .

Vì với mỗi giá trị của x ta xác định được một giá trị y tương ứng nên y là hàm số của x.

b) Số tiền mà người mua phải trả khi mua 10 quả dừa sáp là:

200 000 . 10 = 2 000 000 (đồng).

Vậy số tiền mà người mua phải trả khi mua 10 quả dừa sáp là 2 000 000 đồng.

Bài 5 trang 59 Toán 8 Tập 1: Bác Ninh gửi tiết kiệm 10 triệu đồng ở ngân hàng với kì hạn 12 tháng và không rút tiền trước kì hạn. Lãi suất ngân hàng quy định cho kì hạn 12 tháng là r%/năm.

a) Viết công thức biểu thị số tiền lãi y (đồng) theo lãi suất r%/năm mà bác Ninh nhận được khi hết kì hạn 12 tháng. Hỏi y có phải là hàm số của r hay không? Vì sao?

b) Tính số tiền lãi mà bác Ninh nhận được khi hết kì hạn 12 tháng, biết r = 5,6.

Lời giải:

a) Công thức biểu thị số tiền lãi y (đồng) theo lãi suất r%/năm mà bác Ninh nhận được khi hết kì hạn 12 tháng là: y = 10r% (triệu đồng).

Vì với mỗi giá trị của r thì ta xác định được một giá trị tương ứng của y nên y là hàm số của r.

b) Với r = 5,6 thì số tiền lãi mà bác Ninh nhận được khi hết kì hạn 12 tháng là:

y = 10r% = 10 . 5,6% = 0,56 (triệu đồng) = 560 000 (đồng).

Vậy với r = 5,6 thì số tiền lãi mà bác Ninh nhận được khi hết kì hạn 12 tháng là 560 000 đồng.