Với giải SGK Toán 11 Chân trời sáng tạo trang 49 chi tiết trong Bài 1: Dãy số giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:
Giải Toán 11 trang 49 Tập 1 (Chân trời sáng tạo)

a) Gọi u1 = 25 là số cột gỗ có ở hàng dưới cùng của chồng cột gỗ, un là số cột gỗ có ở hàng thứ n tính từ dưới lên trên. Xét tính tăng, giảm của dãy số này.
b) Gọi vt = 14 là số cột gỗ có ở hàng trên cùng của chồng cột gỗ, vn là số cột gỗ có ở hàng thứ n tính từ trên xuống dưới. Xét tính tăng, giảm của dãy số này.
Lời giải:
a) (un) là số cột gỗ có ở hàng thứ n tính từ dưới lên trên nên (un) là dãy số giảm.
b) (vn) là số cột gỗ có ở hàng thứ n tính từ trên xuống dưới nên (vn) là dãy số tăng.
4. Dãy số bị chặn
Lời giải:
Vì n ∈ ℕ* nên n > 0 do đó > 0 hay un > 0.
Vì n ∈ ℕ* nên n ≥ 1 do đó = 1 hay un ≤ 1.
Do đó 0 < un ≤ 1.
Thực hành 4 trang 49 Toán 11 Tập 1: Xét tính bị chặn của các dãy số sau:
a) (an) với ;
b) (bn) với .
Lời giải:
a) Vì nên , ∀n ∈ ℕ*.
Do đó dãy số (an) bị chặn trên và chặn dưới.
Vì vậy dãy số (an) bị chặn.
b) Ta có:
Vì n ∈ ℕ* nên nên hay bn < 1.
Vì n ∈ ℕ* nên hay bn > 0.
Suy ra 0 < bn < 1. Do đó (bn) là dãy bị chặn trên và chặn dưới.
Vì vậy dãy số (bn) bị chặn.
Xem thêm các bài giải SGK Toán 11 Chân trời sáng tạo hay, chi tiết khác:
Hoạt động khám phá 1 trang 45 Toán 11 Tập 1: Cho hàm số: Tính u(1), u(2), u(50), u(100).
Hoạt động khám phá 2 trang 46 Toán 11 Tập 1: Cho hàm số: Tính v(1), v(2), v(3), v(4), v(5).
Thực hành 1 trang 46 Toán 11 Tập 1: Cho dãy số: Hãy cho biết dãy số trên là hữu hạn hay vô hạn.
Vận dụng 1 trang 46 Toán 11 Tập 1: Cho 5 hình tròn theo thứ tự có bán kính 1; 2; 3; 4; 5.
Thực hành 2 trang 47 Toán 11 Tập 1: Cho dãy số (un) xác định bởi: 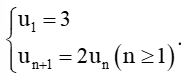
Thực hành 3 trang 48 Toán 11 Tập 1: Xét tính tăng, giảm của các dãy số sau: a) (un) với ;
Thực hành 4 trang 49 Toán 11 Tập 1: Xét tính bị chặn của các dãy số sau:a) (an) với ;
Bài 1 trang 50 Toán 11 Tập 1: Tìm u2, u3 và dự đoán công thức số hạng tổng quát của un dãy số: 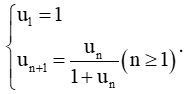
Bài 3 trang 50 Toán 11 Tập 1: Xét tính tăng, giảm của dãy số (yn) với .
Bài 4 trang 50 Toán 11 Tập 1: Xét tính bị chặn của các dãy số sau: a) (an) với ;
Bài 5 trang 50 Toán 11 Tập 1: Cho dãy số (un) với . Chứng minh (un) là dãy số tăng và bị chặn.
Bài 6 trang 50 Toán 11 Tập 1: Cho dãy số (un) với . Tìm các giá trị của a để:a) (un) là dãy số tăng;
Xem thêm lời giải sách giáo khoa Toán 11 Chân trời sáng tạo hay, chi tiết khác:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.