Toptailieu.vn biên soạn và giới thiệu lời giải Toán 11 (Chân trời sáng tạo) Bài 3: Cấp số nhân hay, chi tiết sẽ giúp học sinh dễ dàng trả lời câu hỏi SGK Toán 11 Bài 3 từ đó học tốt môn Toán 11.
Toán 11 (Chân trời sáng tạo) Bài 3: Cấp số nhân
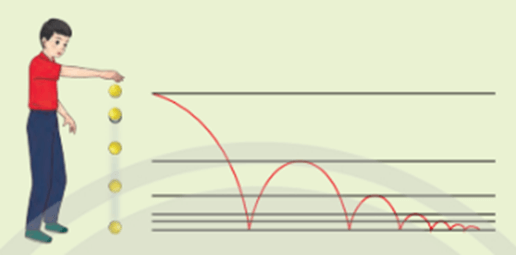
Gọi u1 = 120 là độ cao của lần rơi đầu tiên và u2; u3; u4; ...; un; ... là độ cao của các lần rơi kế tiếp. Tìm 5 số hạng đầu tiên của dãy (un) và tìm điểm đặc biệt của dãy số đó.
Lời giải:
Ta có:
Vì độ cao sau bằng một nửa độ cao của lần rơi trước đó nên ta có:
;
;
;
.
Điểm đặc biệt của dãy số là:
Dãy số giảm dần và mỗi số hạng sau đều bằng tích của số hạng ngay trước nó với một số q không đổi là .
1. Cấp số nhân
b) Tìm điểm giống nhau của các dãy số sau:
i) 3; 6; 12; 24; 48.
ii) .
iii) 2; – 6; 18; – 54; 162; – 486.
Lời giải:
a) Ta có: 2 : 4 = ; 4 : 8 = ; 8 : 16 = ; 16 : 32 = ; 32 : 64 = .
b) Điểm giống nhau của các dãy số sau: kể từ số hạng thứ hai, mỗi số hạng đều bằng tích của số hạng đứng ngay trước nó với một số q không đổi.
i) q = 2;
ii) ;
iii) q = – 3.
Lời giải:
Vì m, n, p theo thứ tự lập thành cấp số cộng nên n = m = p – n = d.
Ta có: 2n : 2m = 2n – m = 2d; 2p : 2n = 2p – n = 2d
Do đó 2n : 2m = 2p : 2n nên đây là một cấp số nhân với công bội q = 2d.
Lời giải:
Dân số năm 2011 là: T1 = P (triệu người).
Năm 2012 là: T2 = P + a%P = (1 + a%).P (triệu người).
Năm 2013 là: T3 = (1 + a%).P + a%(1 + a%).P = (1 + a%)2.P (triệu người).
...
Năm 2021 là: T10 = (1 + a%)10.P (triệu người).
Do đó dãy số dân số các năm từ năm 2011 đến năm 2021 của quốc gia đó tạp thành cấp số nhân với công bội q = 1 + a%.
Lời giải:
Vì tần số của ba phím liên tiếp Sol, La, Si tạo thành một cấp số nhân nên ta có tần số của phím La bằng: .
2. Số hạng tổng quát của cấp số nhân
Lời giải:
Ta có:
u2 = u1.q;
u3 = u2.q = u1.q.q = u1.q2;
u4 = u3.q = u1.q2.q = u1.q3;
u10 = u9.q = u8.q.q = ... = u1.q9.
a) 5; 10; 20; 40; 80; ...
b)
Lời giải:
a) Cấp số nhân 5; 10; 20; 40; 80; ... có số hạng đầu u1 = 5 và công bội q = 2.
Khi đó công thức số hạng tổng quát:
un = u1.qn-1 = 5.2n-1.
b) Cấp số nhân có số hạng đầu u1 = 1 và công bội . Khi đó công thức số hạng tổng quát:
.
a) 690 ngày;
b) 7 314 ngày (khoảng 20 năm).
Lời giải:
Khối lượng nguyên tố poloni 210 lập thành một cấp số cộng với số hạng đầu u1 = 20 gam và công bội q = có số hạng tổng quát là: .
a) Ta có: 690 = 138.5 nên n = 5, khi đó: .
Vậy sau 690 ngày khối lượng còn lại của 20 gam poloni 210 là: 1,25 gam.
b) Ta có: 7 314 = 138.53 nên n = 53, khi đó: .
Vậy sau 7 314 khối lượng còn lại của 20 gam poloni 210 là: 4,4.10-15 gam.
3. Tổng của n số hạng đầu tiên của cấp số nhân
a) So sánh q.Sn và (u2 + u3 + ... + un) + q.un;
b) So sánh u1 + q.Sn và Sn + u1.qn.
Lời giải:
a) Ta có: Snq = (u1 + u2 + ... + un).q = u1q + u2q + u3q + ... + un-1q + unq
= u2 + u3 + u4 + ... + un + unq
= (u2 + u3 + ... + un) + q.un
Vậy q.Sn = (u2 + u3 + ... + un) + q.un.
b) Ta có: u1 + q.Sn = u1 + q.(u1 + u2 + ... + un) = u1 + u1q + u2q + u3q + ... + un-1q + unq
= u1 + u2 + ... + un + unq = = Sn + u1qn-1.q = Sn + u1qn.
Vậy u1 + q.Sn = Sn + u1.qn.
a) u1 = 105; q = 0,1; n = 5;
b) u1 = 10; u2 = – 20; n = 5.
Lời giải:
a) (un) là cấp số nhân có số hạng đầu u1 = 105 và công bội q = 0,1 nên có số hạng tổng quát là: un = u1.qn-1 = 105.(0,1)n – 1 .
Khi đó ta có: u5 = 105.(0,1)5 – 1 = 105.(0,1)4 = 10.
Tổng 5 số hạng đầu tiên của cấp số nhân (un) là:
.
b) (un) là cấp số nhân có số hạng đầu u1 = 10 và công bội q = nên có số hạng tổng quát là: un = u1.qn-1 = 10.(– 2)n – 1 .
Khi đó ta có: u5 = 10.(– 2)5 – 1 = 10.(– 2)4 = 160.
Tổng 5 số hạng đầu tiên của cấp số nhân (un) là:
.
Lời giải:
Dãy số đã cho là một cấp số nhân với số hạng đầu u1 = 120 và công sai .
Khi đó công thức số hạng tổng quát của cấp số nhân này là: un = 120..
Độ cao của quả bóng sau lần rơi thứ 10 là u10 = 120.= .
Tổng độ cao của quả bóng sau 10 lần rơi đầu tiên là:
.
Bài tập
Bài 1 trang 60 Toán 11 Tập 1: Trong các dãy số sau, dãy số nào là cấp số nhân?
a) un = 3.(– 2)n;
b) un = (– 1)n.7n;
c) 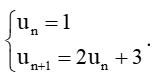
Lời giải:
a) Ta có:
u1 = 3.(0 – 2)1 = 3.(– 2) = – 6.
un+1 = 3.(– 2)n+1 = 3.(– 2)n.(– 2) = un.( – 2).
Vậy dãy số un = 3.(– 2)n là một cấp số nhân có số hạng đầu là u1 = – 6 và công sai d = – 2.
b) Ta có:
u1 = (– 1)1.71 = – 7;
un + 1 = (– 1)n+1.7n+1 = (– 1)n.(– 1).7n.7 = un.(– 7).
Vậy dãy số đã cho là một cấp số nhân có số hạng đầu là u1 = – 7 và công sai d = – 7.
c) Ta có: <; un+1 = 5; un+2 = 13, ...
Dãy số này không phải cấp số nhân vì .
Bài 2 trang 60 Toán 11 Tập 1: Tìm số hạng đầu và công bội của cấp số nhân (un), biết:
a) 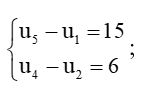 ;
;
b) 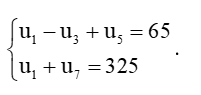 .
.
Lời giải:
a) 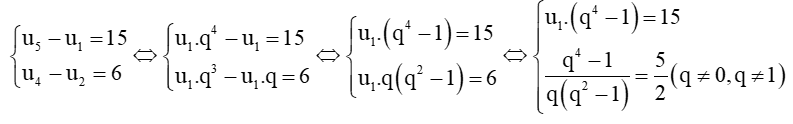
Xét 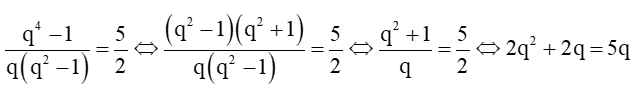
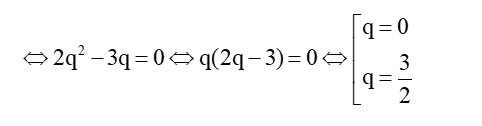
Vì u5 ≠ 0 nên loại q = 0 do đó q = thỏa mãn.
u1 = 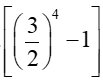 = 15 u1 = .
= 15 u1 = .
Vậy dãy số có số hạng đầu là và công sai q = .
b) 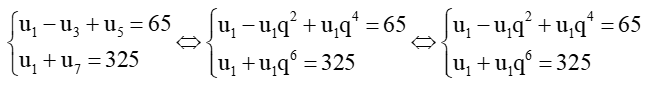
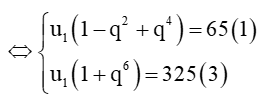
Lấy vế với vế của (1) chia cho (3) ta được
.
⇔ q6 – 5q4 + 5q2 – 4 = 0
⇔ q6 – 4q4 – q4 + 4q2 + q2 – 4 = 0
⇔ q4(q2 – 4) – q2(q2 – 4) + q2 – 4 = 0
⇔ (q2 – 4)(q4 – q2 + 1) = 0
⇔ 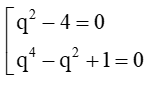
⇔ q = 2 hoặc q4 – q2 + 1 = 0 (vô lí)
Với q = 2 thì u1 = 5.
Với q = – 2 thì u1 = 5.
Vậy cấp số nhân (un) có số hạng đầu là u1 = 5 và công bội là q = 2 hoặc số hạng đầu là u1 = 5 và công bội là q = – 2.
b) Viết sáu số xen giữa các số – 2 và 256 để được cấp số nhân có tám số hạng. Nếu viết tiếp số hạng thứ 15 là bao nhiêu?
Lời giải:
a) Gọi số đo bốn góc của một tứ giác được lập thành một cấp số nhân có công bội q theo thứ tự từ bé đến lớn là: α; β; γ; φ.
Ta có: β = αq, γ = α.q2, φ = α.q3.
Ta lại có: φ = 8α nên q3 = 8 ⇔ q = 2.
Do đó cấp số cộng trên trở thành: α; 2α; 4α; 8α.
Tổng bốn góc trong tứ giác bằng 360° nên α + 2α + 4α + 8α = 360°
⇔ 15α = 360°
⇔ α = 24°
Vậy số đo của các góc trong tứ giác lần lượt là 24°; 48°; 72°; 96°.
b) Cấp số nhân đã cho có u1 = – 2 và u8 = 256.
Ta có: u8 = u1q7 = (– 2).q7 = 256
⇔ q = – 2
Suy ra các số hạng xen giữa hai số – 2 và 256 là: 4; – 8; 16; – 32; 64; – 128.
Số hạng thứ 15 của dãy là: u15 = (– 2).( – 2)14 = (– 2)15 = 0 – 32 768.
Lời giải:
Ta có: là một cấp số cộng nên ta có:
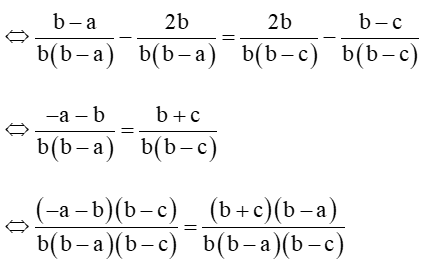
(-a-b)(b-c) = (b+c)(b-a)
⇔ – ab + ac – b2 + bc = b2 – ab + bc – ac
⇔ 2b2 – 2ac = 0
⇔ b2 = ac.
Bài 5 trang 60 Toán 11 Tập 1: Tính các tổng sau:
a) ;
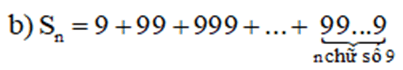
Lời giải:
Dãy số lập thành một cấp số nhân có số hạng đầu u1 = 1 và công bội q = .
Khi đó tổng của n số hạng đầu của cấp số nhân là:
.
Lời giải:
Số lượng vi khuẩn sau mỗi phút lập thành một cấp số nhân (un), với số hạng đầu u1 = 1, công bội q = 2.
Suy ra số hạng tổng quát un = 2n-1.
Vậy sau 20 phút số lượng vi khuẩn trong ống nghiệm là: u20 = 219 (vi khuẩn).
a) Dự đoán dân số của thành phố đó vào năm 2032.
b) Nếu tốc độ gia tăng dân số vẫn giữ nguyên như trên thì ước tính vào năm nào dân số của thành phố đó sẽ tăng gấp đôi so với năm 2022?
Lời giải:
Số dân của thành phố qua các năm với tốc độ gia tăng dân số trung bình mỗi năm là 0,75% lập thành một cấp số nhân (un) với số hạng đầu là u1 = 2,1 (ở năm 2022) và công bội q = 1 + 0,75% = 1,0075 có số hạng tổng quát là: un = 2,1.(1,0075)n-1.
a) Dự đoán dân số của thành phố vào năm 2032 là:
u11 = 2,1.(1,0075)10 ≈ 2,3 triệu người.
b) Dân số của năm thứ n (so với năm 2022) là: 2.2,1 = 4,2 (triệu người).
Ta có: un = 2,1.(1,0075)n-1 = 4,2
⇒ n – 1 ≈ 93
Vậy ước tính vào năm 2022 + 93 = 2115 thì dân số thành phố đó gấp đôi so với năm 2022.
a) Tính độ cao nảy ngược lên của người đó ở lần nảy thứ ba.
b) Tính tổng các độ cao nảy ngược lên của người đó trong 5 lần nảy đầu.

Lời giải:
Độ cao nảy ngược lên của người chơi bungee sau mỗi lần thực hiện cú nhảy lập thành một cấp số nhân có số hạng đầu tiên u1 = 9 và công bội q = 0,06.
Suy ra số hạng tổng quát của cấp số nhân là: un = 9.(0,06)n-1.
a) Độ cao nảy ngược lên của người đó ở lần thứ 3 là:
u3 = 9.(0,06)2 = 1,994.10-3 (m).
b) Tổng các độ cao nảy ngược lên của người đó trong 5 lần nảy đầu là tổng 5 số hạng đầu của cấp số nhân và bằng: .
Xem thêm lời giải sách giáo khoa Toán 11 Chân trời sáng tạo hay, chi tiết khác:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.